Gilbert Strang: Singular Value Decomposition

00:00:00.000 | - So what concept or theorem in linear algebra

00:00:05.000 | or in math you find most beautiful?

00:00:10.680 | That gives you pause that leaves you in awe?

00:00:13.400 | - Well, I'll stick with linear algebra here.

00:00:16.040 | I hope the viewer knows that really,

00:00:18.680 | mathematics is an amazing, amazing subject

00:00:21.400 | and deep, deep connections between ideas

00:00:26.400 | that didn't look connected.

00:00:28.680 | Some, they turned out they were.

00:00:30.600 | But if we stick with linear algebra,

00:00:33.560 | so we have a matrix, that's like the basic thing,

00:00:36.760 | a rectangle of numbers and might be a rectangle of data.

00:00:40.640 | You're probably gonna ask me later about data science

00:00:44.720 | where an often data comes in a matrix.

00:00:48.360 | You have, you know, maybe every column corresponds

00:00:52.920 | to a drug and every row corresponds to a patient

00:00:58.320 | and if the patient reacted favorably to the drug,

00:01:03.320 | then you put up some positive number in there.

00:01:07.160 | Anyway, rectangle of numbers, a matrix is basic.

00:01:12.160 | So the big problem is to understand all those numbers.

00:01:17.200 | You got a big, big set of numbers.

00:01:20.000 | And what are the patterns?

00:01:21.520 | What's going on?

00:01:22.600 | And so one of the ways to break down that matrix

00:01:28.600 | into simple pieces is uses something called singular values.

00:01:33.600 | And that's come on as fundamental in the last,

00:01:40.000 | and certainly in my lifetime.

00:01:42.440 | Eigenvalues, if you have viewers who've done engineering,

00:01:48.000 | math or basic linear algebra, eigenvalues were in there.

00:01:55.040 | But those are restricted to square matrices

00:01:58.200 | and data comes in rectangular matrices.

00:02:00.760 | So you gotta take that next step.

00:02:03.760 | I'm always pushing math faculty, get on, do it, do it,

00:02:08.760 | do it, singular values.

00:02:12.160 | So those are a way to break,

00:02:14.680 | to find the important pieces of the matrix,

00:02:19.680 | which add up to the whole matrix.

00:02:22.920 | So you're breaking a matrix into simple pieces.

00:02:27.080 | And the first piece is the most important part of the data.

00:02:31.280 | The second piece is the second most important part.

00:02:34.160 | And then often, so a data scientist will like,

00:02:39.160 | if a data scientist can find those first and second pieces,

00:02:44.560 | stop there.

00:02:45.840 | The rest of the data is probably round off,

00:02:51.480 | experimental error maybe.

00:02:55.640 | So you're looking for the important part.

00:02:58.200 | - So what do you find beautiful about singular values?

00:03:01.040 | - Well, yeah, I didn't give the theorem.

00:03:04.280 | So here's the idea of singular values.

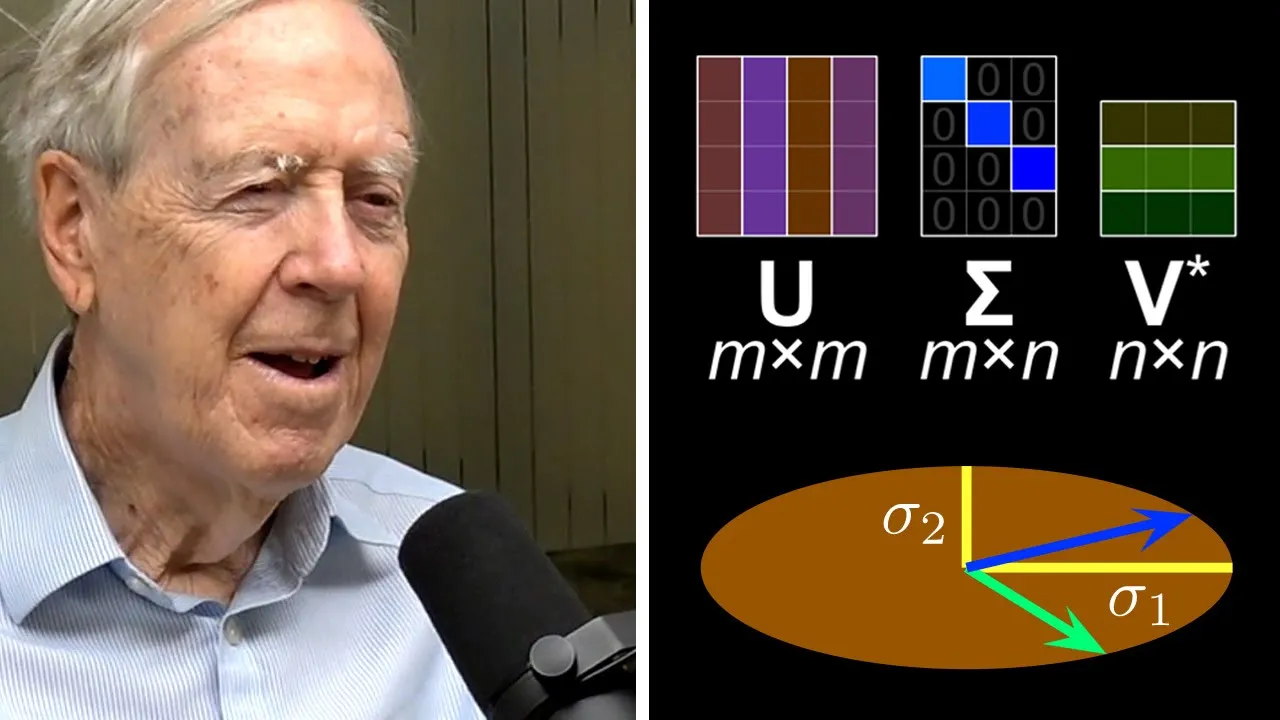
00:03:07.440 | Every matrix, every matrix, rectangular, square, whatever,

00:03:12.440 | it can be written as a product of three very simple,

00:03:16.720 | special matrices.

00:03:18.000 | So that's the theorem.

00:03:19.340 | Every matrix can be written as a rotation times a stretch,

00:03:24.240 | which is just a matrix, a diagonal matrix,

00:03:28.320 | otherwise all zeros except on the one diagonal.

00:03:32.200 | And then the third factor is another rotation.

00:03:36.000 | So rotation, stretch, rotation is the breakup of any matrix.

00:03:41.000 | - The structure of that, the ability that you can do that,

00:03:46.440 | what do you find appealing?

00:03:47.880 | What do you find beautiful about it?

00:03:49.080 | - Well, geometrically, as I freely admit,

00:03:52.240 | the action of a matrix is not so easy to visualize,

00:03:57.240 | but everybody can visualize a rotation.

00:04:00.360 | Take two dimensional space and just turn it

00:04:05.040 | around the center.

00:04:07.280 | Take three dimensional space.

00:04:08.760 | So a pilot has to know about, well, what are the three,

00:04:13.240 | the yaw is one of them.

00:04:14.860 | I've forgotten all the three turns that a pilot makes.

00:04:18.760 | Up to 10 dimensions, you've got 10 ways to turn,

00:04:23.460 | but you can visualize a rotation.

00:04:26.540 | Take the space and turn it, and you can visualize a stretch.

00:04:30.100 | So to break a matrix with all those numbers in it

00:04:35.100 | into something you can visualize,

00:04:39.080 | rotate, stretch, rotate, is pretty neat.

00:04:42.860 | - Yeah. - Pretty neat.

00:04:43.700 | - That's pretty powerful.

00:04:44.940 | (laughs)

00:04:47.020 | (upbeat music)

00:04:49.600 | (upbeat music)

00:04:52.180 | (upbeat music)

00:04:54.760 | (upbeat music)

00:04:57.340 | (upbeat music)

00:04:59.920 | (upbeat music)

00:05:02.500 | (SILENCE)

Gilbert Strang: Singular Value Decomposition

Chapters