- So what concept or theorem in linear algebra or in math you find most beautiful? That gives you pause that leaves you in awe? - Well, I'll stick with linear algebra here. I hope the viewer knows that really, mathematics is an amazing, amazing subject and deep, deep connections between ideas that didn't look connected.

Some, they turned out they were. But if we stick with linear algebra, so we have a matrix, that's like the basic thing, a rectangle of numbers and might be a rectangle of data. You're probably gonna ask me later about data science where an often data comes in a matrix.

You have, you know, maybe every column corresponds to a drug and every row corresponds to a patient and if the patient reacted favorably to the drug, then you put up some positive number in there. Anyway, rectangle of numbers, a matrix is basic. So the big problem is to understand all those numbers.

You got a big, big set of numbers. And what are the patterns? What's going on? And so one of the ways to break down that matrix into simple pieces is uses something called singular values. And that's come on as fundamental in the last, and certainly in my lifetime. Eigenvalues, if you have viewers who've done engineering, math or basic linear algebra, eigenvalues were in there.

But those are restricted to square matrices and data comes in rectangular matrices. So you gotta take that next step. I'm always pushing math faculty, get on, do it, do it, do it, singular values. So those are a way to break, to find the important pieces of the matrix, which add up to the whole matrix.

So you're breaking a matrix into simple pieces. And the first piece is the most important part of the data. The second piece is the second most important part. And then often, so a data scientist will like, if a data scientist can find those first and second pieces, stop there.

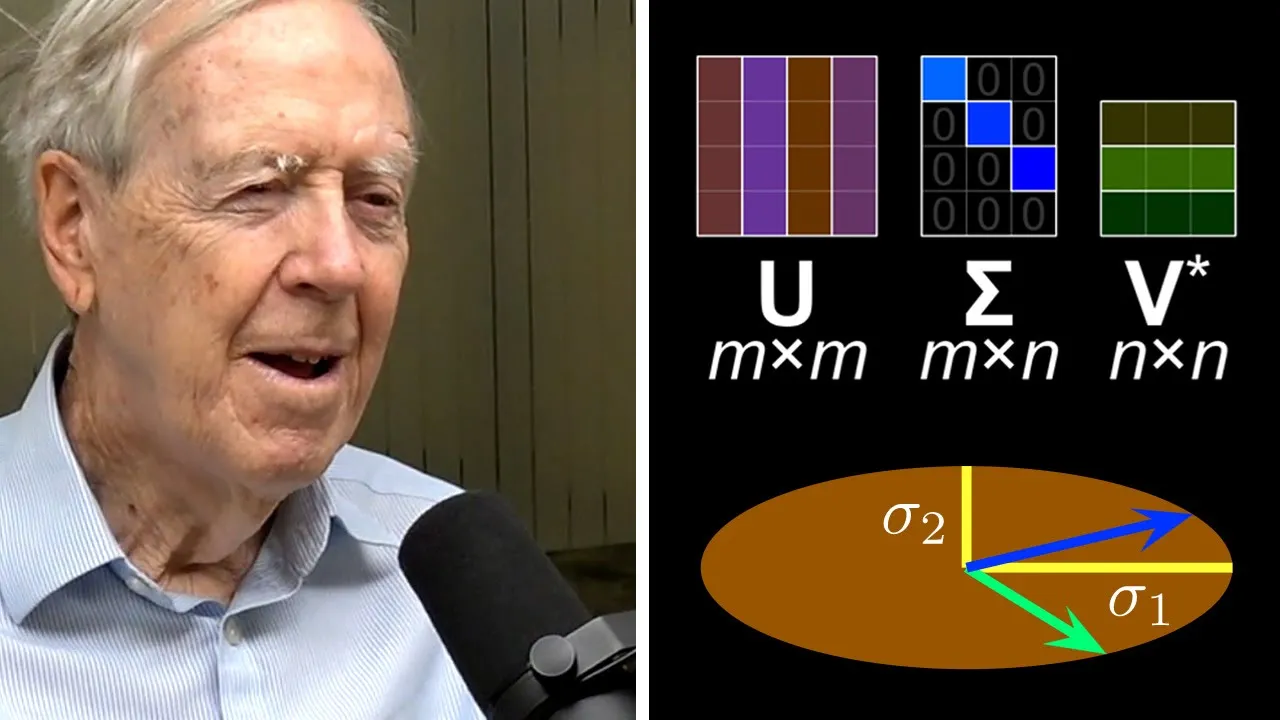
The rest of the data is probably round off, experimental error maybe. So you're looking for the important part. - So what do you find beautiful about singular values? - Well, yeah, I didn't give the theorem. So here's the idea of singular values. Every matrix, every matrix, rectangular, square, whatever, it can be written as a product of three very simple, special matrices.

So that's the theorem. Every matrix can be written as a rotation times a stretch, which is just a matrix, a diagonal matrix, otherwise all zeros except on the one diagonal. And then the third factor is another rotation. So rotation, stretch, rotation is the breakup of any matrix. - The structure of that, the ability that you can do that, what do you find appealing?

What do you find beautiful about it? - Well, geometrically, as I freely admit, the action of a matrix is not so easy to visualize, but everybody can visualize a rotation. Take two dimensional space and just turn it around the center. Take three dimensional space. So a pilot has to know about, well, what are the three, the yaw is one of them.

I've forgotten all the three turns that a pilot makes. Up to 10 dimensions, you've got 10 ways to turn, but you can visualize a rotation. Take the space and turn it, and you can visualize a stretch. So to break a matrix with all those numbers in it into something you can visualize, rotate, stretch, rotate, is pretty neat.

- Yeah. - Pretty neat. - That's pretty powerful. (laughs) (upbeat music) (upbeat music) (upbeat music) (upbeat music) (upbeat music) (upbeat music) (SILENCE)