Building makemore Part 3: Activations & Gradients, BatchNorm

00:00:00.000 | Hi everyone. Today we are continuing our implementation of Makemore.

00:00:03.600 | Now in the last lecture we implemented the multilayer perceptron along the lines of Benji

00:00:07.680 | Hotel 2003 for character level language modeling.

00:00:10.840 | So we followed this paper, took in a few characters in the past, and used an MLP to predict the

00:00:15.240 | next character in a sequence.

00:00:17.420 | So what we'd like to do now is we'd like to move on to more complex and larger neural

00:00:20.880 | networks, like recurrent neural networks and their variations like the GRU, LSTM, and so

00:00:25.200 | on.

00:00:26.200 | Now, before we do that though, we have to stick around the level of multilayer perceptron

00:00:30.320 | for a bit longer.

00:00:31.760 | And I'd like to do this because I would like us to have a very good intuitive understanding

00:00:35.360 | of the activations in the neural net during training, and especially the gradients that

00:00:39.680 | are flowing backwards, and how they behave and what they look like.

00:00:43.120 | This is going to be very important to understand the history of the development of these architectures,

00:00:48.320 | because we'll see that recurrent neural networks, while they are very expressive in that they

00:00:52.360 | are a universal approximator and can in principle implement all the algorithms, we'll see that

00:00:58.400 | they are not very easily optimizable with the first-order gradient-based techniques

00:01:02.040 | that we have available to us and that we use all the time.

00:01:04.960 | And the key to understanding why they are not optimizable easily is to understand the

00:01:10.040 | activations and the gradients and how they behave during training.

00:01:12.920 | And we'll see that a lot of the variants since recurrent neural networks have tried to improve

00:01:17.880 | that situation.

00:01:19.280 | And so that's the path that we have to take, and let's get started.

00:01:23.000 | So the starting code for this lecture is largely the code from before, but I've cleaned it

00:01:26.960 | up a little bit.

00:01:27.960 | So you'll see that we are importing all the Torch and Mathplotlib utilities.

00:01:33.640 | We're reading in the words just like before.

00:01:35.700 | These are eight example words.

00:01:37.360 | There's a total of 32,000 of them.

00:01:39.440 | Here's a vocabulary of all the lowercase letters and the special dot token.

00:01:44.500 | Here we are reading the dataset and processing it and creating three splits, the train, dev,

00:01:51.900 | and the test split.

00:01:52.900 | Now in the MLP, this is the identical same MLP, except you see that I removed a bunch

00:01:57.940 | of magic numbers that we had here.

00:01:59.880 | And instead we have the dimensionality of the embedding space of the characters and

00:02:03.740 | the number of hidden units in the hidden layer.

00:02:06.260 | And so I've pulled them outside here so that we don't have to go and change all these magic

00:02:10.100 | numbers all the time.

00:02:11.820 | With the same neural net with 11,000 parameters that we optimize now over 200,000 steps with

00:02:16.740 | a batch size of 32.

00:02:18.460 | And you'll see that I refactored the code here a little bit, but there are no functional

00:02:23.140 | changes.

00:02:24.140 | I just created a few extra variables, a few more comments, and I removed all the magic

00:02:28.340 | numbers.

00:02:29.540 | And otherwise it's the exact same thing.

00:02:32.100 | Then when we optimize, we saw that our loss looked something like this.

00:02:36.060 | We saw that the train and val loss were about 2.16 and so on.

00:02:41.900 | Here I refactored the code a little bit for the evaluation of arbitrary splits.

00:02:47.220 | So you pass in a string of which split you'd like to evaluate.

00:02:50.220 | And then here, depending on train, val, or test, I index in and I get the correct split.

00:02:55.700 | And then this is the forward pass of the network and evaluation of the loss and printing it.

00:03:00.160 | So just making it nicer.

00:03:03.100 | One thing that you'll notice here is I'm using a decorator torch.nograd, which you can also

00:03:09.260 | look up and read documentation of.

00:03:11.700 | Basically what this decorator does on top of a function is that whatever happens in

00:03:16.060 | this function is assumed by Torch to never require any gradients.

00:03:22.100 | So it will not do any of the bookkeeping that it does to keep track of all the gradients

00:03:26.700 | in anticipation of an eventual backward pass.

00:03:29.760 | It's almost as if all the tensors that get created here have a requires grad of false.

00:03:34.660 | And so it just makes everything much more efficient because you're telling Torch that

00:03:37.420 | I will not call .backward on any of this computation and you don't need to maintain the graph under

00:03:42.180 | the hood.

00:03:43.860 | So that's what this does.

00:03:45.740 | And you can also use a context manager with torch.nograd and you can look those up.

00:03:53.180 | Then here we have the sampling from a model just as before.

00:03:57.100 | So for passive neural net, getting the distribution, sampling from it, adjusting the context window

00:04:02.100 | and repeating until we get the special end token.

00:04:04.980 | And we see that we are starting to get much nicer looking words sampled from the model.

00:04:09.980 | It's still not amazing and they're still not fully name-like, but it's much better than

00:04:14.260 | when we had to do it with the bigram model.

00:04:17.860 | So that's our starting point.

00:04:19.240 | Now the first thing I would like to scrutinize is the initialization.

00:04:22.620 | I can tell that our network is very improperly configured at initialization and there's multiple

00:04:28.260 | things wrong with it, but let's just start with the first one.

00:04:31.300 | Look here on the zeroth iteration, the very first iteration, we are recording a loss of

00:04:36.220 | 27 and this rapidly comes down to roughly one or two or so.

00:04:40.380 | So I can tell that the initialization is all messed up because this is way too high.

00:04:44.500 | In training of neural nets, it is almost always the case that you will have a rough idea for

00:04:48.060 | what loss to expect at initialization, and that just depends on the loss function and

00:04:53.020 | the problem setup.

00:04:54.820 | In this case, I do not expect 27.

00:04:57.060 | I expect a much lower number and we can calculate it together.

00:05:00.900 | Basically at initialization, what we'd like is that there's 27 characters that could come

00:05:06.500 | next for any one training example.

00:05:09.140 | At initialization, we have no reason to believe any characters to be much more likely than

00:05:12.620 | others.

00:05:13.900 | And so we'd expect that the probability distribution that comes out initially is a uniform distribution

00:05:19.100 | assigning about equal probability to all the 27 characters.

00:05:23.540 | So basically what we'd like is the probability for any character would be roughly one over

00:05:29.140 | 27.

00:05:30.140 | That is the probability we should record.

00:05:34.020 | And then the loss is the negative log probability.

00:05:36.740 | So let's wrap this in a tensor and then that one can take the log of it.

00:05:42.160 | And then the negative log probability is the loss we would expect, which is 3.29, much,

00:05:47.820 | much lower than 27.

00:05:50.020 | And so what's happening right now is that at initialization, the neural net is creating

00:05:53.740 | probability distributions that are all messed up.

00:05:56.420 | Some characters are very confident and some characters are very not confident.

00:06:00.780 | And then basically what's happening is that the network is very confidently wrong and

00:06:07.100 | that's what makes it record very high loss.

00:06:10.680 | So here's a smaller four-dimensional example of the issue.

00:06:13.520 | Let's say we only have four characters and then we have logits that come out of the neural

00:06:18.180 | net and they are very, very close to zero.

00:06:21.000 | Then when we take the softmax of all zeros, we get probabilities that are a diffuse distribution.

00:06:27.500 | So sums to one and is exactly uniform.

00:06:31.220 | And then in this case, if the label is say two, it doesn't actually matter if the label

00:06:36.080 | is two or three or one or zero because it's a uniform distribution.

00:06:40.000 | We're recording the exact same loss in this case, 1.38.

00:06:43.200 | So this is the loss we would expect for a four-dimensional example.

00:06:46.360 | And I can see of course that as we start to manipulate these logits, we're going to be

00:06:50.920 | changing the loss here.

00:06:52.560 | So it could be that we luck out and by chance this could be a very high number like five

00:06:58.040 | or something like that.

00:06:59.040 | Then in that case, we'll record a very low loss because we're assigning the correct probability

00:07:02.740 | at initialization by chance to the correct label.

00:07:06.840 | Much more likely it is that some other dimension will have a high logit.

00:07:14.120 | And then what will happen is we start to record a much higher loss.

00:07:17.240 | And what can happen is basically the logits come out like something like this, and they

00:07:22.360 | take on extreme values and we record really high loss.

00:07:28.640 | For example, if we have torq.random of four.

00:07:31.760 | So these are normally distributed numbers, four of them.

00:07:40.560 | Then here we can also print the logits, probabilities that come out of it and loss.

00:07:47.160 | And so because these logits are near zero, for the most part, the loss that comes out

00:07:51.800 | is okay.

00:07:54.040 | But suppose this is like times 10 now.

00:07:58.880 | You see how because these are more extreme values, it's very unlikely that you're going

00:08:03.040 | to be guessing the correct bucket and then you're confidently wrong and recording very

00:08:08.160 | high loss.

00:08:09.780 | If your logits are coming out even more extreme, you might get extremely insane losses like

00:08:15.520 | infinity even at initialization.

00:08:20.560 | So basically this is not good and we want the logits to be roughly zero when the network

00:08:26.640 | is initialized.

00:08:27.640 | In fact, the logits don't have to be just zero, they just have to be equal.

00:08:31.360 | So for example, if all the logits are one, then because of the normalization inside the

00:08:35.520 | softmax, this will actually come out okay.

00:08:38.640 | But by symmetry, we don't want it to be any arbitrary positive or negative number.

00:08:42.180 | We just want it to be all zeros and record the loss that we expect at initialization.

00:08:46.520 | So let's now concretely see where things go wrong in our example.

00:08:49.040 | Here we have the initialization.

00:08:51.720 | Let me reinitialize the neural net.

00:08:53.640 | And here let me break after the very first iteration so we only see the initial loss,

00:08:58.080 | which is 27.

00:09:00.280 | So that's way too high.

00:09:01.280 | And intuitively now we can expect the variables involved and we see that the logits here,

00:09:06.040 | if we just print some of these, if we just print the first row, we see that the logits

00:09:11.740 | take on quite extreme values.

00:09:14.040 | And that's what's creating the fake confidence in incorrect answers and makes the loss get

00:09:20.880 | very, very high.

00:09:22.220 | So these logits should be much, much closer to zero.

00:09:25.520 | So now let's think through how we can achieve logits coming out of this neural net to be

00:09:30.120 | more closer to zero.

00:09:32.680 | You see here that logits are calculated as the hidden states multiplied by W2 plus B2.

00:09:37.800 | So first of all, currently we're initializing B2 as random values of the right size.

00:09:44.500 | But because we want roughly zero, we don't actually want to be adding a bias of random

00:09:48.840 | numbers.

00:09:49.840 | So I'm going to add a times a zero here to make sure that B2 is just basically zero at

00:09:55.760 | initialization.

00:09:57.620 | And second, this is H multiplied by W2.

00:10:00.500 | So if we want logits to be very, very small, then we would be multiplying W2 and making

00:10:05.000 | that smaller.

00:10:07.140 | So for example, if we scale down W2 by 0.1, all the elements, then if I do again just

00:10:13.260 | the very first iteration, you see that we are getting much closer to what we expect.

00:10:17.480 | So roughly what we want is about 3.29.

00:10:20.600 | This is 4.2.

00:10:21.600 | I can make this maybe even smaller.

00:10:24.600 | 3.32.

00:10:25.600 | Okay, so we're getting closer and closer.

00:10:28.760 | Now you're probably wondering, can we just set this to zero?

00:10:33.320 | Then we get, of course, exactly what we're looking for at initialization.

00:10:38.360 | And the reason I don't usually do this is because I'm very nervous, and I'll show you

00:10:42.840 | in a second why you don't want to be setting W's or weights of a neural net exactly to

00:10:47.680 | zero.

00:10:48.680 | You usually want it to be small numbers instead of exactly zero.

00:10:53.480 | For this output layer in this specific case, I think it would be fine, but I'll show you

00:10:57.840 | in a second where things go wrong very quickly if you do that.

00:11:00.840 | So let's just go with 0.01.

00:11:03.040 | In that case, our loss is close enough, but has some entropy.

00:11:06.760 | It's not exactly zero.

00:11:08.580 | It's got some little entropy, and that's used for symmetry breaking, as we'll see in a second.

00:11:12.800 | The logits are now coming out much closer to zero, and everything is well and good.

00:11:18.320 | So if I just erase these, and I now take away the break statement, we can run the optimization

00:11:26.520 | with this new initialization.

00:11:28.560 | And let's just see what losses we record.

00:11:32.120 | Okay, so I let it run, and you see that we started off good, and then we came down a

00:11:36.520 | bit.

00:11:38.400 | The plot of the loss now doesn't have this hockey-shape appearance, because basically

00:11:44.040 | what's happening in the hockey stick, the very first few iterations of the loss, what's

00:11:48.200 | happening during the optimization is the optimization is just squashing down the logits, and then

00:11:53.160 | it's rearranging the logits.

00:11:55.180 | So basically, we took away this easy part of the loss function where just the weights

00:11:59.880 | were just being shrunk down.

00:12:02.120 | And so therefore, we don't get these easy gains in the beginning, and we're just getting

00:12:06.500 | some of the hard gains of training the actual neural net, and so there's no hockey stick

00:12:10.080 | appearance.

00:12:11.560 | So good things are happening in that both, number one, loss at initialization is what

00:12:15.680 | we expect, and the loss doesn't look like a hockey stick.

00:12:20.880 | And this is true for any neural net you might train, and something to look out for.

00:12:25.720 | And second, the loss that came out is actually quite a bit improved.

00:12:29.600 | Unfortunately, I erased what we had here before.

00:12:31.920 | I believe this was 2.12, and this was 2.16.

00:12:37.400 | So we get a slightly improved result, and the reason for that is because we're spending

00:12:42.240 | more cycles, more time, optimizing the neural net actually, instead of just spending the

00:12:48.180 | first several thousand iterations probably just squashing down the weights, because they

00:12:53.560 | are so way too high in the beginning of the initialization.

00:12:56.940 | So something to look out for, and that's number one.

00:13:00.120 | Now let's look at the second problem.

00:13:01.880 | Let me reinitialize our neural net, and let me reintroduce the break statement, so we

00:13:06.680 | have a reasonable initial loss.

00:13:08.680 | So even though everything is looking good on the level of the loss, and we get something

00:13:11.480 | that we expect, there's still a deeper problem lurking inside this neural net and its initialization.

00:13:17.560 | So the logits are now okay.

00:13:19.960 | The problem now is with the values of h, the activations of the hidden states.

00:13:25.440 | Now if we just visualize this vector, sorry, this tensor h, it's kind of hard to see, but

00:13:30.480 | the problem here, roughly speaking, is you see how many of the elements are 1 or -1?

00:13:36.080 | Now recall that torch.10h, the 10h function, is a squashing function.

00:13:40.600 | It takes arbitrary numbers and it squashes them into a range of -1 and 1, and it does

00:13:44.600 | so smoothly.

00:13:46.260 | So let's look at the histogram of h to get a better idea of the distribution of the values

00:13:50.720 | inside this tensor.

00:13:52.420 | We can do this first.

00:13:55.120 | Well we can see that h is 32 examples and 200 activations in each example.

00:14:00.920 | We can view it as -1, stretch it out into one large vector, and we can then call toList

00:14:08.600 | to convert this into one large Python list of floats.

00:14:13.800 | And then we can pass this into plt.hist for histogram, and we say we want 50 bins, and

00:14:20.160 | a semicolon to suppress a bunch of output we don't want.

00:14:24.440 | So we see this histogram, and we see that most of the values by far take on value of

00:14:28.760 | -1 and 1.

00:14:30.160 | So this 10h is very, very active.

00:14:33.360 | And we can also look at basically why that is.

00:14:37.940 | We can look at the preactivations that feed into the 10h, and we can see that the distribution

00:14:44.080 | of the preactivations is very, very broad.

00:14:47.480 | These take numbers between -15 and 15, and that's why in a torch.10h everything is being

00:14:52.440 | squashed and capped to be in the range of -1 and 1, and lots of numbers here take on

00:14:56.960 | very extreme values.

00:14:59.200 | Now if you are new to neural networks, you might not actually see this as an issue.

00:15:03.480 | But if you're well-versed in the dark arts of backpropagation and have an intuitive sense

00:15:07.840 | of how these gradients flow through a neural net, you are looking at your distribution

00:15:11.680 | of 10h activations here, and you are sweating.

00:15:15.040 | So let me show you why.

00:15:16.440 | We have to keep in mind that during backpropagation, just like we saw in micrograd, we are doing

00:15:20.320 | backward pass starting at the loss and flowing through the network backwards.

00:15:24.800 | In particular, we're going to backpropagate through this torch.10h.

00:15:28.920 | And this layer here is made up of 200 neurons for each one of these examples, and it implements

00:15:34.960 | an element-wise 10h.

00:15:36.720 | So let's look at what happens in 10h in the backward pass.

00:15:39.860 | We can actually go back to our previous micrograd code in the very first lecture and see how

00:15:44.840 | we implemented 10h.

00:15:46.960 | We saw that the input here was x, and then we calculate t, which is the 10h of x.

00:15:52.320 | So that's t.

00:15:53.320 | And t is between -1 and 1.

00:15:54.760 | It's the output of the 10h.

00:15:56.600 | And then in the backward pass, how do we backpropagate through a 10h?

00:16:00.200 | We take out.grad, and then we multiply it, this is the chain rule, with the local gradient,

00:16:06.280 | which took the form of 1 - t^2.

00:16:09.120 | So what happens if the outputs of your 10h are very close to -1 or 1?

00:16:14.160 | If you plug in t = 1 here, you're going to get a 0, multiplying out.grad.

00:16:19.800 | No matter what out.grad is, we are killing the gradient, and we're stopping, effectively,

00:16:24.880 | the backpropagation through this 10h unit.

00:16:27.360 | Similarly, when t is -1, this will again become 0, and out.grad just stops.

00:16:33.140 | And intuitively, this makes sense, because this is a 10h neuron, and what's happening

00:16:38.440 | is if its output is very close to 1, then we are in the tail of this 10h.

00:16:44.120 | And so changing, basically, the input is not going to impact the output of the 10h too

00:16:51.400 | much, because it's in a flat region of the 10h.

00:16:55.840 | And so therefore, there's no impact on the loss.

00:16:58.660 | And so indeed, the weights and the biases along with this 10h neuron do not impact the

00:17:04.720 | loss, because the output of this 10h unit is in the flat region of the 10h, and there's

00:17:09.000 | no influence.

00:17:10.280 | We can be changing them however we want, and the loss is not impacted.

00:17:14.960 | That's another way to justify that, indeed, the gradient would be basically 0.

00:17:19.200 | It vanishes.

00:17:20.960 | Indeed, when t equals 0, we get 1 times out.grad.

00:17:27.520 | So when the 10h takes on exactly value of 0, then out.grad is just passed through.

00:17:35.040 | So basically what this is doing is if t is equal to 0, then the 10h unit is inactive,

00:17:42.640 | and a gradient just passes through.

00:17:44.960 | But the more you are in the flat tails, the more the gradient is squashed.

00:17:49.620 | So in fact, you'll see that the gradient flowing through 10h can only ever decrease,

00:17:54.680 | and the amount that it decreases is proportional through a square here, depending on how far

00:18:02.120 | you are in the flat tails of this 10h.

00:18:05.200 | And so that's kind of what's happening here.

00:18:07.440 | And the concern here is that if all of these outputs h are in the flat regions of negative

00:18:14.040 | 1 and 1, then the gradients that are flowing through the network will just get destroyed

00:18:18.960 | at this layer.

00:18:21.200 | Now there is some redeeming quality here, and that we can actually get a sense of the

00:18:25.520 | problem here as follows.

00:18:26.920 | I wrote some code here.

00:18:29.400 | Basically what we want to do here is we want to take a look at h, take the absolute value,

00:18:34.920 | and see how often it is in the flat region, so say greater than 0.99.

00:18:42.520 | And what you get is the following.

00:18:44.500 | And this is a Boolean tensor.

00:18:45.960 | So in the Boolean tensor, you get a white if this is true and a black if this is false.

00:18:52.640 | And so basically what we have here is the 32 examples and the 200 hidden neurons.

00:18:57.560 | And we see that a lot of this is white.

00:19:00.460 | And what that's telling us is that all these 10h neurons were very, very active, and they're

00:19:07.080 | in the flat tail.

00:19:09.160 | And so in all these cases, the backward gradient would get destroyed.

00:19:16.600 | Now we would be in a lot of trouble if for any one of these 200 neurons, if it was the

00:19:22.960 | case that the entire column is white, because in that case, we have what's called a dead

00:19:27.920 | neuron.

00:19:28.920 | And this could be a 10h neuron where the initialization of the weights and the biases could be such

00:19:32.640 | that no single example ever activates this 10h in the sort of active part of the 10h.

00:19:40.040 | If all the examples land in the tail, then this neuron will never learn.

00:19:44.800 | It is a dead neuron.

00:19:46.840 | And so just scrutinizing this and looking for columns of completely white, we see that

00:19:52.800 | this is not the case.

00:19:54.280 | So I don't see a single neuron that is all of white.

00:19:59.520 | And so therefore, it is the case that for every one of these 10h neurons, we do have

00:20:04.640 | some examples that activate them in the active part of the 10h.

00:20:09.080 | And so some gradients will flow through, and this neuron will learn.

00:20:12.520 | And the neuron will change, and it will move, and it will do something.

00:20:16.520 | But you can sometimes get yourself in cases where you have dead neurons.

00:20:20.440 | And the way this manifests is that for a 10h neuron, this would be when no matter what

00:20:25.600 | inputs you plug in from your data set, this 10h neuron always fires completely one or

00:20:30.000 | completely negative one.

00:20:31.460 | And then it will just not learn, because all the gradients will be just zeroed out.

00:20:36.800 | This is true not just for 10h, but for a lot of other nonlinearities that people use in

00:20:40.240 | neural networks.

00:20:41.280 | So we certainly use 10h a lot, but sigmoid will have the exact same issue, because it

00:20:45.600 | is a squashing neuron.

00:20:47.640 | And so the same will be true for sigmoid, but basically the same will actually apply

00:20:55.920 | to sigmoid.

00:20:57.160 | The same will also apply to a ReLU.

00:20:59.300 | So ReLU has a completely flat region here below zero.

00:21:03.580 | So if you have a ReLU neuron, then it is a pass-through if it is positive.

00:21:08.760 | And if the pre-activation is negative, it will just shut it off.

00:21:12.840 | Since the region here is completely flat, then during backpropagation, this would be

00:21:18.120 | exactly zeroing out the gradient.

00:21:21.160 | All of the gradient would be set exactly to zero instead of just a very, very small number

00:21:24.560 | depending on how positive or negative t is.

00:21:28.660 | And so you can get, for example, a dead ReLU neuron.

00:21:31.680 | And a dead ReLU neuron would basically look like-- basically what it is is if a neuron

00:21:37.520 | with a ReLU nonlinearity never activates.

00:21:41.320 | So for any examples that you plug in in the dataset, it never turns on.

00:21:45.360 | It's always in this flat region.

00:21:47.600 | Then this ReLU neuron is a dead neuron.

00:21:49.640 | Its weights and bias will never learn.

00:21:52.160 | They will never get a gradient because the neuron never activated.

00:21:55.880 | And this can sometimes happen at initialization because the weights and the biases just make

00:21:59.440 | it so that by chance some neurons are just forever dead.

00:22:03.000 | But it can also happen during optimization.

00:22:05.020 | If you have like a too high of a learning rate, for example, sometimes you have these

00:22:08.280 | neurons that get too much of a gradient and they get knocked out of the data manifold.

00:22:13.820 | And what happens is that from then on, no example ever activates this neuron.

00:22:18.000 | So this neuron remains dead forever.

00:22:19.640 | So it's kind of like a permanent brain damage in a mind of a network.

00:22:24.040 | And so sometimes what can happen is if your learning rate is very high, for example, and

00:22:27.520 | you have a neural net with ReLU neurons, you train the neural net and you get some last

00:22:31.920 | loss.

00:22:32.920 | And then actually what you do is you go through the entire training set and you forward your

00:22:38.440 | examples and you can find neurons that never activate.

00:22:42.160 | They are dead neurons in your network.

00:22:44.200 | And so those neurons will never turn on.

00:22:46.580 | And usually what happens is that during training, these ReLU neurons are changing, moving, etc.

00:22:50.820 | And then because of a high gradient somewhere by chance, they get knocked off and then nothing

00:22:55.300 | ever activates them.

00:22:56.500 | And from then on, they are just dead.

00:22:59.120 | So that's kind of like a permanent brain damage that can happen to some of these neurons.

00:23:03.320 | These other nonlinearities like Leaky ReLU will not suffer from this issue as much because

00:23:07.560 | you can see that it doesn't have flat tails.

00:23:10.720 | You'll almost always get gradients.

00:23:13.200 | And ELU is also fairly frequently used.

00:23:16.600 | It also might suffer from this issue because it has flat parts.

00:23:20.400 | So that's just something to be aware of and something to be concerned about.

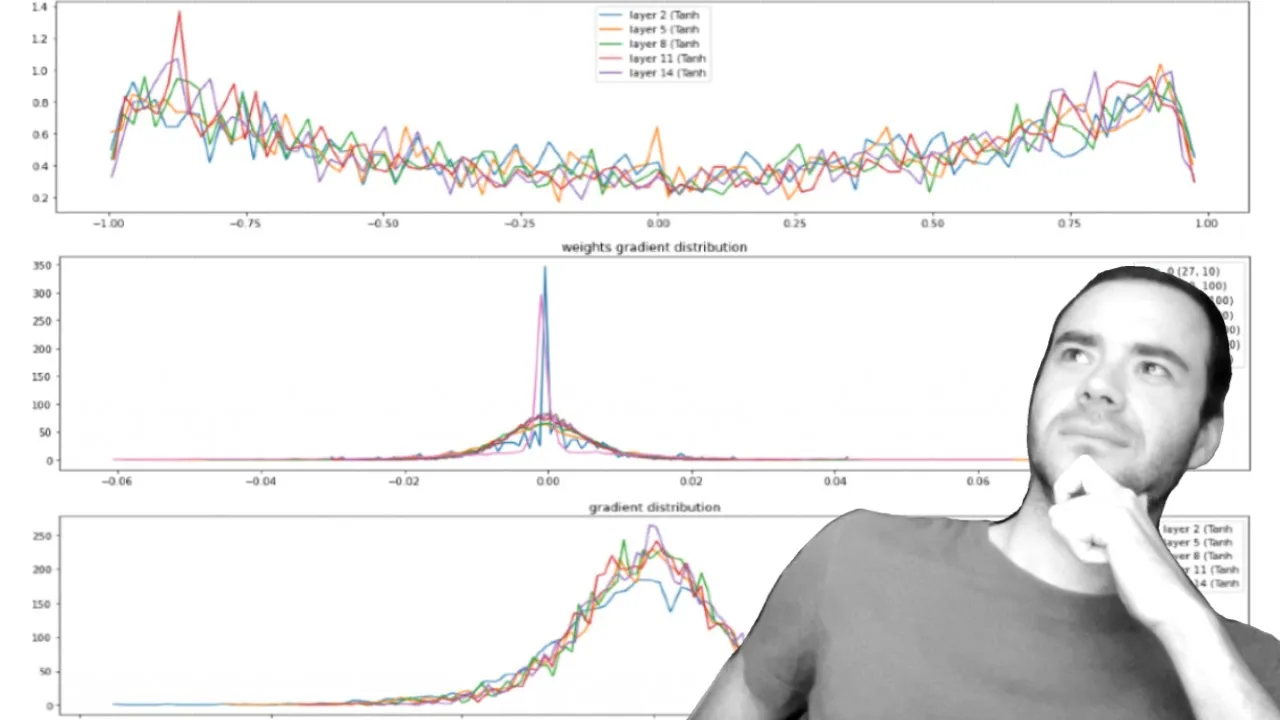
00:23:24.240 | And in this case, we have way too many activations h that take on extreme values.

00:23:30.640 | And because there's no column of white, I think we will be okay.

00:23:34.440 | And indeed, the network optimizes and gives us a pretty decent loss.

00:23:37.740 | But it's just not optimal.

00:23:39.040 | And this is not something you want, especially during initialization.

00:23:42.400 | And so basically what's happening is that this h pre-activation that's flowing to 10h,

00:23:49.080 | it's too extreme.

00:23:50.080 | It's too large.

00:23:51.080 | It's creating a distribution that is too saturated in both sides of the 10h.

00:23:57.400 | And it's not something you want because it means that there's less training for these

00:24:01.600 | neurons because they update less frequently.

00:24:05.820 | So how do we fix this?

00:24:06.820 | Well, h pre-activation is mcat, which comes from c.

00:24:12.660 | So these are uniform Gaussian.

00:24:15.040 | But then it's multiplied by w1 plus b1.

00:24:17.680 | And h pre-act is too far off from 0, and that's causing the issue.

00:24:21.600 | So we want this pre-activation to be closer to 0, very similar to what we had with logits.

00:24:27.440 | So here, we want actually something very, very similar.

00:24:31.480 | Now it's okay to set the biases to a very small number.

00:24:35.080 | We can either multiply by 001 to get a little bit of entropy.

00:24:39.540 | I sometimes like to do that just so that there's a little bit of variation and diversity in

00:24:45.920 | the original initialization of these 10h neurons.

00:24:49.600 | And I find in practice that that can help optimization a little bit.

00:24:54.000 | And then the weights, we can also just squash.

00:24:56.360 | So let's multiply everything by 0.1.

00:24:59.400 | Let's rerun the first batch.

00:25:01.680 | And now let's look at this.

00:25:03.360 | And well, first let's look at here.

00:25:07.120 | You see now, because we multiplied w by 0.1, we have a much better histogram.

00:25:11.280 | And that's because the pre-activations are now between -1.5 and 1.5.

00:25:15.160 | And this, we expect much, much less white.

00:25:17.520 | Okay, there's no white.

00:25:21.000 | So basically, that's because there are no neurons that saturated above 0.99 in either

00:25:26.760 | direction.

00:25:27.760 | So it's actually a pretty decent place to be.

00:25:32.200 | Maybe we can go up a little bit.

00:25:35.160 | Sorry, am I changing w1 here?

00:25:38.880 | So maybe we can go to 0.2.

00:25:42.200 | Okay, so maybe something like this is a nice distribution.

00:25:46.560 | So maybe this is what our initialization should be.

00:25:49.280 | So let me now erase these.

00:25:53.640 | And let me, starting with initialization, let me run the full optimization without the

00:25:59.360 | break.

00:26:00.720 | And let's see what we get.

00:26:02.840 | Okay, so the optimization finished.

00:26:04.920 | And I rerun the loss.

00:26:06.300 | And this is the result that we get.

00:26:08.200 | And then just as a reminder, I put down all the losses that we saw previously in this

00:26:11.120 | lecture.

00:26:12.560 | So we see that we actually do get an improvement here.

00:26:15.280 | And just as a reminder, we started off with a validation loss of 2.17 when we started.

00:26:20.160 | By fixing the softmax being confidently wrong, we came down to 2.13.

00:26:24.200 | And by fixing the 10H layer being way too saturated, we came down to 2.10.

00:26:29.000 | And the reason this is happening, of course, is because our initialization is better.

00:26:32.040 | And so we're spending more time doing productive training instead of not very productive training

00:26:37.920 | because our gradients are set to zero, and we have to learn very simple things like the

00:26:43.400 | overconfidence of the softmax in the beginning.

00:26:45.600 | And we're spending cycles just like squashing down the weight matrix.

00:26:49.120 | So this is illustrating basically initialization and its impact on performance just by being

00:26:56.360 | aware of the internals of these neural nets and their activations and their gradients.

00:27:00.640 | Now we're working with a very small network.

00:27:03.000 | This is just one layer multilayer perceptron.

00:27:05.640 | So because the network is so shallow, the optimization problem is actually quite easy

00:27:09.920 | and very forgiving.

00:27:11.600 | So even though our initialization was terrible, the network still learned eventually.

00:27:15.520 | It just got a bit worse result.

00:27:17.480 | This is not the case in general, though.

00:27:19.560 | Once we actually start working with much deeper networks that have, say, 50 layers, things

00:27:24.880 | can get much more complicated.

00:27:27.400 | And these problems stack up.

00:27:30.600 | And so you can actually get into a place where the network is basically not training at all

00:27:35.080 | if your initialization is bad enough.

00:27:37.520 | And the deeper your network is and the more complex it is, the less forgiving it is to

00:27:41.600 | some of these errors.

00:27:43.200 | And so something to definitely be aware of and something to scrutinize, something to

00:27:48.760 | plot and something to be careful with.

00:27:51.400 | And yeah.

00:27:52.400 | Okay, so that's great that that worked for us.

00:27:55.860 | But what we have here now is all these magic numbers like 0.2.

00:27:59.200 | Like where do I come up with this?

00:28:00.800 | And how am I supposed to set these if I have a large neural network with lots and lots

00:28:03.840 | of layers?

00:28:05.440 | And so obviously no one does this by hand.

00:28:07.660 | There's actually some relatively principled ways of setting these scales that I would

00:28:12.200 | like to introduce to you now.

00:28:14.160 | So let me paste some code here that I prepared just to motivate the discussion of this.

00:28:19.660 | So what I'm doing here is we have some random input here, X, that is drawn from a Gaussian.

00:28:25.520 | And there's 1,000 examples that are 10-dimensional.

00:28:28.920 | And then we have a weighting layer here that is also initialized using Gaussian, just like

00:28:33.360 | we did here.

00:28:35.000 | And these neurons in the hidden layer look at 10 inputs, and there are 200 neurons in

00:28:40.280 | this hidden layer.

00:28:41.800 | And then we have here, just like here in this case, the multiplication, X multiplied by

00:28:46.760 | W to get the pre-activations of these neurons.

00:28:51.000 | And basically the analysis here looks at, okay, suppose these are uniform Gaussian and

00:28:55.560 | these weights are uniform Gaussian.

00:28:57.300 | If I do X times W, and we forget for now the bias and the nonlinearity, then what is the

00:29:04.040 | mean and the standard deviation of these Gaussians?

00:29:07.080 | So in the beginning here, the input is just a normal Gaussian distribution.

00:29:11.160 | Mean is zero, and the standard deviation is one.

00:29:13.720 | And the standard deviation, again, is just the measure of a spread of this Gaussian.

00:29:18.680 | But then once we multiply here and we look at the histogram of Y, we see that the mean,

00:29:24.360 | of course, stays the same.

00:29:25.800 | It's about zero, because this is a symmetric operation.

00:29:28.980 | But we see here that the standard deviation has expanded to three.

00:29:32.680 | So the input standard deviation was one, but now we've grown to three.

00:29:35.840 | And so what you're seeing in the histogram is that this Gaussian is expanding.

00:29:41.240 | And so we're expanding this Gaussian from the input.

00:29:45.920 | And we don't want that.

00:29:46.920 | We want most of the neural net to have relatively similar activations.

00:29:50.680 | So unit Gaussian, roughly, throughout the neural net.

00:29:53.480 | And so the question is, how do we scale these Ws to preserve this distribution to remain

00:30:02.160 | a Gaussian?

00:30:03.900 | And so intuitively, if I multiply here these elements of W by a larger number, let's say

00:30:09.680 | by five, then this Gaussian grows and grows in standard deviation.

00:30:16.040 | So now we're at 15.

00:30:17.440 | So basically, these numbers here in the output, Y, take on more and more extreme values.

00:30:22.680 | But if we scale it down, let's say 0.2, then conversely, this Gaussian is getting smaller

00:30:28.800 | and smaller.

00:30:29.800 | And it's shrinking.

00:30:30.800 | And you can see that the standard deviation is 0.6.

00:30:34.080 | And so the question is, what do I multiply by here to exactly preserve the standard deviation

00:30:39.440 | to be one?

00:30:41.160 | And it turns out that the correct answer mathematically, when you work out through the variance of this

00:30:45.880 | multiplication here, is that you are supposed to divide by the square root of the fan in.

00:30:52.840 | The fan in is basically the number of input elements here, 10.

00:30:58.180 | So we are supposed to divide by 10 square root.

00:31:01.000 | And this is one way to do the square root.

00:31:02.560 | You raise it to a power of 0.5.

00:31:04.600 | That's the same as doing a square root.

00:31:07.300 | So when you divide by the square root of 10, then we see that the output Gaussian, it has

00:31:14.500 | exactly standard deviation of 1.

00:31:17.560 | Now unsurprisingly, a number of papers have looked into how to best initialize neural

00:31:22.360 | networks.

00:31:23.640 | And in the case of multilayer perceptrons, we can have fairly deep networks that have

00:31:27.080 | these nonlinearities in between.

00:31:29.400 | And we want to make sure that the activations are well-behaved and they don't expand to

00:31:32.880 | infinity or shrink all the way to 0.

00:31:35.420 | And the question is, how do we initialize the weights so that these activations take

00:31:38.280 | on reasonable values throughout the network?

00:31:41.040 | Now one paper that has studied this in quite a bit of detail that is often referenced is

00:31:45.100 | this paper by Kaiming et al. called Delving Deep Interactive Fires.

00:31:49.440 | Now in this case, they actually studied convolutional neural networks.

00:31:52.520 | And they studied especially the ReLU nonlinearity and the pReLU nonlinearity instead of a 10H

00:31:59.440 | nonlinearity.

00:32:00.440 | But the analysis is very similar.

00:32:01.940 | And basically what happens here is for them, the ReLU nonlinearity that they care about

00:32:07.980 | quite a bit here is a squashing function where all the negative numbers are simply clamped

00:32:14.740 | to 0.

00:32:16.000 | So the positive numbers are a path through, but everything negative is just set to 0.

00:32:20.740 | And because you're basically throwing away half of the distribution, they find in their

00:32:25.300 | analysis of the forward activations in the neural net that you have to compensate for

00:32:29.500 | that with a gain.

00:32:32.220 | And so here, they find that basically when they initialize their weights, they have to

00:32:37.340 | do it with a zero-mean Gaussian whose standard deviation is square root of 2 over the Fannin.

00:32:43.540 | What we have here is we are initializing the Gaussian with the square root of Fannin.

00:32:49.140 | This NL here is the Fannin.

00:32:50.700 | So what we have is square root of 1 over the Fannin because we have the division here.

00:32:58.200 | Now they have to add this factor of 2 because of the ReLU, which basically discards half

00:33:02.860 | of the distribution and clamps it at 0.

00:33:05.580 | And so that's where you get an initial factor.

00:33:08.060 | Now in addition to that, this paper also studies not just the behavior of the activations in

00:33:13.540 | the forward pass of the neural net, but it also studies the backpropagation.

00:33:17.860 | And we have to make sure that the gradients also are well-behaved because ultimately,

00:33:23.580 | they end up updating our parameters.

00:33:25.900 | And what they find here through a lot of the analysis that I invite you to read through,

00:33:29.620 | but it's not exactly approachable, what they find is basically if you properly initialize

00:33:35.140 | the forward pass, the backward pass is also approximately initialized up to a constant

00:33:40.380 | factor that has to do with the size of the number of hidden neurons in an early and late

00:33:46.980 | layer.

00:33:49.940 | But basically they find empirically that this is not a choice that matters too much.

00:33:54.100 | Now this kyming initialization is also implemented in PyTorch.

00:33:58.160 | So if you go to torch.nn.init documentation, you'll find kyming normal.

00:34:02.620 | And in my opinion, this is probably the most common way of initializing neural networks

00:34:06.140 | now.

00:34:07.140 | And it takes a few keyword arguments here.

00:34:09.900 | So number one, it wants to know the mode.

00:34:13.020 | Would you like to normalize the activations or would you like to normalize the gradients

00:34:17.220 | to be always Gaussian with zero mean and a unit or one standard deviation?

00:34:22.820 | And because they find in the paper that this doesn't matter too much, most of the people

00:34:25.680 | just leave it as the default, which is fan-in.

00:34:28.380 | And then second, passing the nonlinearity that you are using.

00:34:31.600 | Because depending on the nonlinearity, we need to calculate a slightly different gain.

00:34:36.060 | And so if your nonlinearity is just linear, so there's no nonlinearity, then the gain

00:34:41.140 | here will be one.

00:34:42.140 | And we have the exact same kind of formula that we've got up here.

00:34:46.420 | But if the nonlinearity is something else, we're going to get a slightly different gain.

00:34:49.920 | And so if we come up here to the top, we see that, for example, in the case of ReLU, this

00:34:54.420 | gain is a square root of two.

00:34:56.420 | And the reason it's a square root is because in this paper, you see how the two is inside

00:35:05.060 | of the square root, so the gain is a square root of two.

00:35:09.120 | In the case of linear or identity, we just get a gain of one.

00:35:13.860 | In the case of 10H, which is what we're using here, the advised gain is a five over three.

00:35:19.000 | And intuitively, why do we need a gain on top of the initialization?

00:35:22.720 | It's because 10H, just like ReLU, is a contractive transformation.

00:35:27.520 | So what that means is you're taking the output distribution from this matrix multiplication,

00:35:31.740 | and then you are squashing it in some way.

00:35:33.720 | Now ReLU squashes it by taking everything below zero and clamping it to zero.

00:35:37.560 | 10H also squashes it because it's a contractive operation.

00:35:40.360 | It will take the tails and it will squeeze them in.

00:35:44.360 | And so in order to fight the squeezing in, we need to boost the weights a little bit

00:35:48.940 | so that we renormalize everything back to unit standard deviation.

00:35:53.520 | So that's why there's a little bit of a gain that comes out.

00:35:56.640 | Now I'm skipping through this section a little bit quickly, and I'm doing that actually intentionally.

00:36:01.060 | And the reason for that is because about seven years ago when this paper was written, you

00:36:06.280 | had to actually be extremely careful with the activations and the gradients and their

00:36:09.820 | ranges and their histograms.

00:36:11.860 | And you had to be very careful with the precise setting of gains and the scrutinizing of the

00:36:15.160 | nonlinearities used and so on.

00:36:17.260 | And everything was very finicky and very fragile and to be very properly arranged for the neural

00:36:21.680 | net to train, especially if your neural net was very deep.

00:36:24.960 | But there are a number of modern innovations that have made everything significantly more

00:36:27.760 | stable and more well-behaved.

00:36:29.720 | And it's become less important to initialize these networks exactly right.

00:36:34.120 | And some of those modern innovations, for example, are residual connections, which we

00:36:37.600 | will cover in the future.

00:36:39.200 | The use of a number of normalization layers, like for example, batch normalization, layer

00:36:45.080 | normalization, group normalization, we're going to go into a lot of these as well.

00:36:49.080 | And number three, much better optimizers, not just stochastic gradient descent, the

00:36:52.480 | simple optimizer we're basically using here, but slightly more complex optimizers like

00:36:57.360 | RMSProp and especially Adam.

00:36:59.760 | And so all of these modern innovations make it less important for you to precisely calibrate

00:37:03.960 | the initialization of the neural net.

00:37:06.180 | All that being said, in practice, what should we do?

00:37:09.740 | In practice, when I initialize these neural nets, I basically just normalize my weights

00:37:13.720 | by the square root of the fan-in.

00:37:16.000 | So basically, roughly what we did here is what I do.

00:37:20.320 | Now, if we want to be exactly accurate here, and go back in it of timing normal, this is

00:37:28.000 | how we would implement it.

00:37:29.720 | We want to set the standard deviation to be gain over the square root of fan-in.

00:37:35.500 | So to set the standard deviation of our weights, we will proceed as follows.

00:37:41.560 | Basically when we have a torsion type random, and let's say I just create a thousand numbers,

00:37:46.000 | we can look at the standard deviation of this, and of course that's one.

00:37:48.840 | That's the amount of spread.

00:37:49.840 | Let's make this a bit bigger so it's closer to one.

00:37:52.480 | So that's the spread of the Gaussian of zero mean and unit standard deviation.

00:37:58.120 | Now basically when you take these and you multiply by say 0.2, that basically scales

00:38:03.320 | down the Gaussian and that makes its standard deviation 0.2.

00:38:07.120 | So basically the number that you multiply by here ends up being the standard deviation

00:38:10.320 | of this Gaussian.

00:38:12.280 | So here this is a standard deviation 0.2 Gaussian here when we sample RW1.

00:38:19.400 | But we want to set the standard deviation to gain over square root of fan-in.

00:38:26.160 | So in other words, we want to multiply by gain, which for 10H is 5/3.

00:38:32.400 | 5/3 is the gain, and then times, or I guess sorry, divide square root of the fan-in.

00:38:51.720 | In this example here the fan-in was 10, and I just noticed that actually here the fan-in

00:38:56.200 | for W1 is actually an embed times block size, which as you will recall is actually 30.

00:39:01.960 | And that's because each character is 10-dimensional, but then we have three of them and we concatenate

00:39:05.480 | them.

00:39:06.480 | So actually the fan-in here was 30, and I should have used 30 here probably.

00:39:10.240 | But basically we want 30 square root.

00:39:13.320 | So this is the number, this is what our standard deviation we want to be, and this number turns

00:39:17.680 | out to be 0.3.

00:39:19.680 | Whereas here just by fiddling with it and looking at the distribution and making sure

00:39:22.880 | it looks okay, we came up with 0.2.

00:39:26.040 | And so instead what we want to do here is we want to make the standard deviation be

00:39:29.960 | 5/3, which is our gain, divide this amount times 0.2 square root.

00:39:41.400 | And these brackets here are not that necessary, but I'll just put them here for clarity.

00:39:46.220 | This is basically what we want.

00:39:47.580 | This is the kyming init in our case for 10H nonlinearity, and this is how we would initialize

00:39:53.400 | the neural net.

00:39:54.880 | And so we're multiplying by 0.3 instead of multiplying by 0.2.

00:40:01.120 | And so we can initialize this way, and then we can train the neural net and see what we

00:40:07.160 | get.

00:40:08.160 | Okay, so I trained the neural net and we end up in roughly the same spot.

00:40:12.340 | So looking at the validation loss, we now get 2.10, and previously we also had 2.10.

00:40:17.680 | There's a little bit of a difference, but that's just the randomness of the process,

00:40:20.240 | I suspect.

00:40:21.600 | But the big deal, of course, is we get to the same spot, but we did not have to introduce

00:40:26.080 | any magic numbers that we got from just looking at histograms and guessing, checking.

00:40:32.540 | We have something that is semi-principled and will scale us to much bigger networks

00:40:37.080 | and something that we can sort of use as a guide.

00:40:40.260 | So I mentioned that the precise setting of these initializations is not as important

00:40:44.160 | today due to some modern innovations.

00:40:46.080 | And I think now is a pretty good time to introduce one of those modern innovations, and that

00:40:49.520 | is batch normalization.

00:40:51.320 | So batch normalization came out in 2015 from a team at Google, and it was an extremely

00:40:57.000 | impactful paper because it made it possible to train very deep neural nets quite reliably,

00:41:03.080 | and it basically just worked.

00:41:05.240 | So here's what batch normalization does and what's implemented.

00:41:10.320 | Basically we have these hidden states, H_preact, right?

00:41:13.840 | And we were talking about how we don't want these preactivation states to be way too small

00:41:20.400 | because then the tanh is not doing anything, but we don't want them to be too large because

00:41:25.320 | then the tanh is saturated.

00:41:27.640 | In fact, we want them to be roughly Gaussian, so zero mean and a unit or one standard deviation,

00:41:34.160 | at least at initialization.

00:41:36.200 | So the insight from the batch normalization paper is, okay, you have these hidden states

00:41:41.160 | and you'd like them to be roughly Gaussian, then why not take the hidden states and just

00:41:46.440 | normalize them to be Gaussian?

00:41:49.000 | And it sounds kind of crazy, but you can just do that because standardizing hidden states

00:41:55.280 | so that they're unit Gaussian is a perfectly differentiable operation, as we'll soon see.

00:41:59.760 | And so that was kind of like the big insight in this paper, and when I first read it, my

00:42:03.280 | mind was blown because you can just normalize these hidden states, and if you'd like unit

00:42:07.480 | Gaussian states in your network, at least initialization, you can just normalize them

00:42:12.680 | to be unit Gaussian.

00:42:14.360 | So let's see how that works.

00:42:16.600 | So we're going to scroll to our pre-activations here just before they enter into the tanh.

00:42:21.560 | Now the idea again is, remember, we're trying to make these roughly Gaussian, and that's

00:42:25.240 | because if these are way too small numbers, then the tanh here is kind of inactive.

00:42:30.560 | But if these are very large numbers, then the tanh is way too saturated and gradient

00:42:35.360 | is no flow.

00:42:36.600 | So we'd like this to be roughly Gaussian.

00:42:39.280 | So the insight in batch normalization again is that we can just standardize these activations

00:42:44.280 | so they are exactly Gaussian.

00:42:47.000 | So here, H_preact has a shape of 32 by 200, 32 examples by 200 neurons in the hidden layer.

00:42:56.120 | So basically what we can do is we can take H_preact and we can just calculate the mean,

00:43:01.480 | and the mean we want to calculate across the 0th dimension, and we want to also keep the

00:43:06.800 | missed true so that we can easily broadcast this.

00:43:11.760 | So the shape of this is 1 by 200.

00:43:14.880 | In other words, we are doing the mean over all the elements in the batch.

00:43:21.040 | And similarly, we can calculate the standard deviation of these activations, and that will

00:43:27.280 | also be 1 by 200.

00:43:29.560 | Now in this paper, they have the sort of prescription here, and see here we are calculating the

00:43:36.280 | mean, which is just taking the average value of any neuron's activation, and then the standard

00:43:44.480 | deviation is basically kind of like the measure of the spread that we've been using, which

00:43:50.360 | is the distance of every one of these values away from the mean, and that squared and averaged.

00:44:00.320 | That's the variance, and then if you want to take the standard deviation, you would

00:44:03.680 | square root the variance to get the standard deviation.

00:44:07.880 | So these are the two that we're calculating, and now we're going to normalize or standardize

00:44:12.640 | these x's by subtracting the mean and dividing by the standard deviation.

00:44:17.980 | So basically, we're taking H_preact and we subtract the mean, and then we divide by the

00:44:31.600 | standard deviation.

00:44:34.520 | This is exactly what these two, std and mean, are calculating.

00:44:41.080 | This is the mean and this is the variance.

00:44:43.160 | You see how the sigma is the standard deviation usually, so this is sigma squared, which the

00:44:47.040 | variance is the square of the standard deviation.

00:44:51.040 | So this is how you standardize these values, and what this will do is that every single

00:44:54.920 | neuron now, and its firing rate, will be exactly unit Gaussian on these 32 examples at least

00:45:00.920 | of this batch.

00:45:01.920 | That's why it's called batch normalization.

00:45:03.400 | We are normalizing these batches.

00:45:06.920 | And then we could, in principle, train this.

00:45:09.720 | Notice that calculating the mean and your standard deviation, these are just mathematical

00:45:13.360 | formulas.

00:45:14.360 | They're perfectly differentiable.

00:45:15.360 | All of this is perfectly differentiable, and we can just train this.

00:45:18.860 | The problem is you actually won't achieve a very good result with this, and the reason

00:45:23.520 | for that is we want these to be roughly Gaussian, but only at initialization.

00:45:29.840 | But we don't want these to be forced to be Gaussian always.

00:45:34.520 | We'd like to allow the neural net to move this around to potentially make it more diffuse,

00:45:39.360 | to make it more sharp, to make some 10H neurons maybe be more trigger happy or less trigger

00:45:44.640 | happy.

00:45:45.640 | So we'd like this distribution to move around, and we'd like the backpropagation to tell

00:45:49.000 | us how the distribution should move around.

00:45:52.540 | And so in addition to this idea of standardizing the activations at any point in the network,

00:45:59.400 | we have to also introduce this additional component in the paper here described as scale

00:46:04.480 | and shift.

00:46:05.480 | And so basically what we're doing is we're taking these normalized inputs, and we are

00:46:09.640 | additionally scaling them by some gain and offsetting them by some bias to get our final

00:46:15.480 | output from this layer.

00:46:17.920 | And so what that amounts to is the following.

00:46:20.520 | We are going to allow a batch normalization gain to be initialized at just a once, and

00:46:27.760 | the once will be in the shape of 1 by n hidden.

00:46:32.560 | And then we also will have a bn_bias, which will be torched at zeros, and it will also

00:46:38.400 | be of the shape 1 by n hidden.

00:46:42.400 | And then here, the bn_gain will multiply this, and the bn_bias will offset it here.

00:46:51.280 | So because this is initialized to 1 and this to 0, at initialization, each neuron's firing

00:46:58.080 | values in this batch will be exactly unit Gaussian and will have nice numbers.

00:47:03.680 | No matter what the distribution of the H_preact is coming in, coming out, it will be unit

00:47:08.240 | Gaussian for each neuron, and that's roughly what we want, at least at initialization.

00:47:14.040 | And then during optimization, we'll be able to backpropagate to bn_gain and bn_bias and

00:47:18.600 | change them so the network is given the full ability to do with this whatever it wants

00:47:23.360 | internally.

00:47:25.960 | Here we just have to make sure that we include these in the parameters of the neural net

00:47:32.160 | because they will be trained with backpropagation.

00:47:35.860 | So let's initialize this, and then we should be able to train.

00:47:45.800 | And then we're going to also copy this line, which is the batch normalization layer here

00:47:52.040 | on a single line of code, and we're going to swing down here, and we're also going to

00:47:56.440 | do the exact same thing at test time here.

00:48:01.840 | So similar to train time, we're going to normalize and then scale, and that's going to give us

00:48:07.520 | our train and validation loss.

00:48:10.880 | And we'll see in a second that we're actually going to change this a little bit, but for

00:48:13.240 | now I'm going to keep it this way.

00:48:15.720 | So I'm just going to wait for this to converge.

00:48:17.400 | Okay, so I allowed the neural nets to converge here, and when we scroll down, we see that

00:48:21.400 | our validation loss here is 2.10, roughly, which I wrote down here.

00:48:26.500 | And we see that this is actually kind of comparable to some of the results that we've achieved

00:48:29.560 | previously.

00:48:30.560 | Now, I'm not actually expecting an improvement in this case, and that's because we are dealing

00:48:35.800 | with a very simple neural net that has just a single hidden layer.

00:48:39.520 | So in fact, in this very simple case of just one hidden layer, we were able to actually

00:48:43.800 | calculate what the scale of W should be to make these preactivations already have a roughly

00:48:49.240 | Gaussian shape.

00:48:50.240 | So the batch normalization is not doing much here.

00:48:53.360 | But you might imagine that once you have a much deeper neural net that has lots of different

00:48:57.000 | types of operations, and there's also, for example, residual connections, which we'll

00:49:01.240 | cover, and so on, it will become basically very, very difficult to tune the scales of

00:49:07.120 | your weight matrices such that all the activations throughout the neural net are roughly Gaussian.

00:49:13.140 | And so that's going to become very quickly intractable.

00:49:16.160 | But compared to that, it's going to be much, much easier to sprinkle batch normalization

00:49:20.160 | layers throughout the neural net.

00:49:22.240 | So in particular, it's common to look at every single linear layer like this one.

00:49:27.060 | This is a linear layer multiplying by a weight matrix and adding a bias.

00:49:31.000 | Or for example, convolutions, which we'll cover later and also perform basically a multiplication

00:49:36.240 | with a weight matrix, but in a more spatially structured format.

00:49:41.080 | It's customary to take this linear layer or convolutional layer and append a batch normalization

00:49:46.040 | layer right after it to control the scale of these activations at every point in the

00:49:50.760 | neural net.

00:49:51.960 | So we'd be adding these batch normal layers throughout the neural net.

00:49:54.960 | And then this controls the scale of these activations throughout the neural net.

00:49:58.720 | It doesn't require us to do perfect mathematics and care about the activation distributions

00:50:03.920 | for all these different types of neural network Lego building blocks that you might want to

00:50:07.760 | introduce into your neural net.

00:50:09.560 | And it significantly stabilizes the training.

00:50:12.400 | And that's why these layers are quite popular.

00:50:14.960 | Now the stability offered by batch normalization actually comes at a terrible cost.

00:50:19.160 | And that cost is that if you think about what's happening here, something terribly strange

00:50:24.120 | and unnatural is happening.

00:50:26.580 | It used to be that we have a single example feeding into a neural net, and then we calculate

00:50:32.040 | its activations and its logits.

00:50:34.560 | And this is a deterministic sort of process.

00:50:37.560 | So you arrive at some logits for this example.

00:50:40.260 | And then because of efficiency of training, we suddenly started to use batches of examples.

00:50:44.940 | But those batches of examples were processed independently, and it was just an efficiency

00:50:48.720 | thing.

00:50:50.000 | But now suddenly in batch normalization, because of the normalization through the batch, we

00:50:53.760 | are coupling these examples mathematically and in the forward pass and the backward pass

00:50:58.040 | of the neural net.

00:50:59.640 | So now the hidden state activations, HPREACT, and your logits for any one input example

00:51:05.560 | are not just a function of that example and its input, but they're also a function of

00:51:09.760 | all the other examples that happen to come for a ride in that batch.

00:51:14.640 | And these examples are sampled randomly.

00:51:16.620 | And so what's happening is, for example, when you look at HPREACT, that's going to feed

00:51:19.420 | into H, the hidden state activations, for example, for any one of these input examples,

00:51:25.400 | is going to actually change slightly depending on what other examples there are in the batch.

00:51:31.040 | And depending on what other examples happen to come for a ride, H is going to change suddenly

00:51:36.300 | and is going to jitter if you imagine sampling different examples, because the statistics

00:51:40.840 | of the mean and the standard deviation are going to be impacted.

00:51:44.120 | And so you'll get a jitter for H, and you'll get a jitter for logits.

00:51:48.760 | And you'd think that this would be a bug or something undesirable, but in a very strange

00:51:53.840 | way, this actually turns out to be good in neural network training as a side effect.

00:51:59.840 | And the reason for that is that you can think of this as kind of like a regularizer, because

00:52:04.200 | what's happening is you have your input and you get your H, and then depending on the

00:52:07.200 | other examples, this is jittering a bit.

00:52:10.080 | And so what that does is that it's effectively padding out any one of these input examples,

00:52:14.440 | and it's introducing a little bit of entropy.

00:52:16.720 | And because of the padding out, it's actually kind of like a form of data augmentation,

00:52:21.480 | which we'll cover in the future.

00:52:22.480 | And it's kind of like augmenting the input a little bit and jittering it, and that makes

00:52:27.360 | it harder for the neural nets to overfit to these concrete specific examples.

00:52:32.120 | So by introducing all this noise, it actually like pads out the examples and it regularizes

00:52:36.800 | the neural net.

00:52:37.960 | And that's one of the reasons why deceivingly as a second order effect, this is actually

00:52:42.680 | a regularizer, and that has made it harder for us to remove the use of batch normalization.

00:52:48.920 | Because basically no one likes this property that the examples in the batch are coupled

00:52:53.240 | mathematically and in the forward pass.

00:52:55.960 | And it leads to all kinds of like strange results.

00:52:58.840 | We'll go into some of that in a second as well.

00:53:01.960 | And it leads to a lot of bugs and so on.

00:53:05.000 | And so no one likes this property.

00:53:07.180 | And so people have tried to deprecate the use of batch normalization and move to other

00:53:11.720 | normalization techniques that do not couple the examples of a batch.

00:53:15.280 | Examples are layer normalization, instance normalization, group normalization, and so

00:53:19.440 | on.

00:53:20.440 | And we'll come or we'll come or some of these later.

00:53:24.400 | But basically long story short, batch normalization was the first kind of normalization layer

00:53:28.120 | to be introduced.

00:53:29.300 | It worked extremely well.

00:53:31.080 | It happens to have this regularizing effect.

00:53:33.600 | It stabilized training and people have been trying to remove it and move to some of the

00:53:38.880 | other normalization techniques.

00:53:41.080 | But it's been hard because it just works quite well.

00:53:44.480 | And some of the reason that it works quite well is again because of this regularizing

00:53:47.560 | effect and because it is quite effective at controlling the activations and their distributions.

00:53:54.640 | So that's kind of like the brief story of batch normalization.

00:53:57.700 | And I'd like to show you one of the other weird sort of outcomes of this coupling.

00:54:03.880 | So here's one of the strange outcomes that I only glossed over previously when I was

00:54:08.120 | evaluating the loss on the validation set.

00:54:11.160 | Basically once we've trained a neural net, we'd like to deploy it in some kind of a setting

00:54:15.920 | and we'd like to be able to feed in a single individual example and get a prediction out

00:54:19.840 | from our neural net.

00:54:21.560 | But how do we do that when our neural net now in a forward pass estimates the statistics

00:54:25.840 | of the mean understated deviation of a batch?

00:54:28.040 | The neural net expects batches as an input now.

00:54:30.640 | So how do we feed in a single example and get sensible results out?

00:54:34.600 | And so the proposal in the batch normalization paper is the following.

00:54:39.040 | What we would like to do here is we would like to basically have a step after training

00:54:44.800 | that calculates and sets the batch norm mean and standard deviation a single time over

00:54:50.720 | the training set.

00:54:52.360 | And so I wrote this code here in the interest of time and we're going to call what's called

00:54:56.720 | calibrate the batch norm statistics.

00:54:59.280 | And basically what we do is Torch.nograd telling PyTorch that none of this we will call a dot

00:55:05.360 | backward on and it's going to be a bit more efficient.

00:55:09.000 | We're going to take the training set, get the preactivations for every single training

00:55:12.600 | example and then one single time estimate the mean and standard deviation over the entire

00:55:16.760 | training set.

00:55:18.360 | And then we're going to get B and mean and B and standard deviation.

00:55:21.100 | And now these are fixed numbers estimating over the entire training set.

00:55:25.440 | And here instead of estimating it dynamically, we are going to instead here use B and mean

00:55:34.460 | and here we're just going to use B and standard deviation.

00:55:38.220 | And so at test time, we are going to fix these, clamp them and use them during inference.

00:55:43.280 | And now you see that we get basically identical result.

00:55:49.120 | But the benefit that we've gained is that we can now also forward a single example because

00:55:53.480 | the mean and standard deviation are now fixed sort of tensors.

00:55:57.560 | That said, nobody actually wants to estimate this mean and standard deviation as a second

00:56:01.800 | stage after neural network training because everyone is lazy.

00:56:05.820 | And so this batch normalization paper actually introduced one more idea, which is that we

00:56:10.680 | can estimate the mean and standard deviation in a running manner during training of the

00:56:15.960 | neural net.

00:56:17.280 | And then we can simply just have a single stage of training.

00:56:20.240 | And on the side of that training, we are estimating the running mean and standard deviation.

00:56:24.640 | So let's see what that would look like.

00:56:26.160 | Let me basically take the mean here that we are estimating on the batch and let me call

00:56:30.600 | this B and mean on the i-th iteration.

00:56:35.520 | And then here, this is B and STD.

00:56:41.180 | B and STD at i.

00:56:47.300 | And the mean comes here and the STD comes here.

00:56:53.100 | So so far, I've done nothing.

00:56:54.180 | I've just moved around and I created these extra variables for the mean and standard

00:56:57.500 | deviation and I've put them here.

00:56:59.860 | So so far, nothing has changed.

00:57:01.840 | But what we're going to do now is we're going to keep a running mean of both of these values

00:57:05.400 | during training.

00:57:06.400 | So let me swing up here and let me create a B and mean underscore running.

00:57:12.020 | And I'm going to initialize it at zeros and then B and STD running, which I'll initialize

00:57:19.580 | at ones.

00:57:23.540 | Because in the beginning, because of the way we initialized W1 and B1, HPREACT will be

00:57:30.000 | roughly unit Gaussian, so the mean will be roughly zero and the standard deviation roughly

00:57:33.920 | one.

00:57:34.920 | So I'm going to initialize these that way.

00:57:37.280 | But then here, I'm going to update these.

00:57:39.560 | And in PyTorch, these mean and standard deviation that are running, they're not actually part

00:57:46.220 | of the gradient based optimization.

00:57:47.800 | We're never going to derive gradients with respect to them.

00:57:50.800 | They're updated on the side of training.

00:57:53.740 | And so what we're going to do here is we're going to say with torch.nograd, telling PyTorch

00:57:58.720 | that the update here is not supposed to be building out a graph because there will be

00:58:03.360 | no dot backward.

00:58:05.480 | But this running mean is basically going to be 0.999 times the current value plus 0.001

00:58:15.160 | times this value, this new mean.

00:58:20.640 | And in the same way, BNSTDRunning will be mostly what it used to be, but it will receive

00:58:29.400 | a small update in the direction of what the current standard deviation is.

00:58:35.180 | And as you're seeing here, this update is outside and on the side of the gradient based

00:58:39.940 | optimization.

00:58:41.480 | And it's simply being updated not using gradient descent, it's just being updated using a janky,

00:58:46.640 | like smooth, sort of running mean manner.

00:58:53.360 | And so while the network is training and these preactivations are sort of changing and shifting

00:58:58.120 | around during backpropagation, we are keeping track of the typical mean and standard deviation

00:59:03.680 | and we're estimating them once.

00:59:05.640 | And when I run this, now I'm keeping track of this in a running manner.

00:59:12.160 | And what we're hoping for, of course, is that the BNMean_running and BNMean_backpropagation

00:59:16.520 | or STD are going to be very similar to the ones that we calculated here before.

00:59:22.480 | And that way, we don't need a second stage because we've sort of combined the two stages

00:59:26.800 | and we've put them on the side of each other, if you want to look at it that way.

00:59:30.800 | And this is how this is also implemented in the batch normalization layer in PyTorch.

00:59:35.100 | So during training, the exact same thing will happen.

00:59:39.120 | And then later when you're using inference, it will use the estimated running mean of

00:59:43.720 | both the mean and standard deviation of those hidden states.

00:59:47.960 | So let's wait for the optimization to converge and hopefully the running mean and standard

00:59:51.760 | deviation are roughly equal to these two.

00:59:53.960 | And then we can simply use it here and we don't need this stage of explicit calibration

00:59:58.360 | at the end.

00:59:59.360 | Okay, so the optimization finished.

01:00:01.280 | I'll rerun the explicit estimation.

01:00:03.980 | And then the BNMean from the explicit estimation is here.

01:00:07.880 | And BNMean from the running estimation during the optimization, you can see is very, very

01:00:14.760 | similar.

01:00:15.760 | It's not identical, but it's pretty close.

01:00:19.720 | And in the same way, BNSTD is this and BNSTDRunning is this.

01:00:26.440 | As you can see that once again, they are fairly similar values, not identical, but pretty

01:00:30.600 | close.

01:00:31.960 | And so then here, instead of BNMean, we can use the BNMean running.

01:00:36.160 | Instead of BNSTD, we can use BNSTDRunning.

01:00:40.120 | And hopefully the validation loss will not be impacted too much.

01:00:43.720 | Okay, so basically identical.

01:00:46.880 | And this way, we've eliminated the need for this explicit stage of calibration because

01:00:51.800 | we are doing it in line over here.

01:00:53.760 | Okay, so we're almost done with batch normalization.

01:00:56.160 | There are only two more notes that I'd like to make.

01:00:58.600 | Number one, I've skipped a discussion over what is this plus epsilon doing here.

01:01:02.280 | This epsilon is usually like some small fixed number, for example, 1E negative 5 by default.

01:01:07.360 | And what it's doing is that it's basically preventing a division by zero in the case

01:01:11.120 | that the variance over your batch is exactly zero.

01:01:15.940 | In that case, here we'd normally have a division by zero, but because of the plus epsilon,

01:01:20.880 | this is going to become a small number in the denominator instead, and things will be

01:01:24.080 | more well-behaved.

01:01:25.680 | So feel free to also add a plus epsilon here of a very small number.

01:01:29.200 | It doesn't actually substantially change the result.

01:01:31.200 | I'm going to skip it in our case just because this is unlikely to happen in our very simple

01:01:34.840 | example here.

01:01:35.840 | And the second thing I want you to notice is that we're being wasteful here, and it's

01:01:39.920 | very subtle.

01:01:41.400 | But right here where we are adding the bias into HPREACT, these biases now are actually

01:01:47.160 | useless because we're adding them to the HPREACT.

01:01:50.600 | But then we are calculating the mean for every one of these neurons and subtracting it.

01:01:56.080 | So whatever bias you add here is going to get subtracted right here.

01:02:00.940 | And so these biases are not doing anything.

01:02:02.920 | In fact, they're being subtracted out, and they don't impact the rest of the calculation.

01:02:07.360 | So if you look at B1.grad, it's actually going to be zero because it's being subtracted out

01:02:11.620 | and doesn't actually have any effect.

01:02:13.720 | And so whenever you're using batch normalization layers, then if you have any weight layers

01:02:17.640 | before, like a linear or a conv or something like that, you're better off coming here and

01:02:22.380 | just not using bias.

01:02:24.400 | So you don't want to use bias, and then here you don't want to add it because that's spurious.

01:02:30.720 | Instead we have this batch normalization bias here, and that batch normalization bias is

01:02:35.320 | now in charge of the biasing of this distribution instead of this B1 that we had here originally.

01:02:42.320 | And so basically the batch normalization layer has its own bias, and there's no need to have

01:02:47.560 | a bias in the layer before it because that bias is going to be subtracted out anyway.

01:02:52.080 | So that's the other small detail to be careful with.

01:02:54.160 | Sometimes it's not going to do anything catastrophic.

01:02:56.760 | This B1 will just be useless.

01:02:58.600 | It will never get any gradient.

01:03:00.440 | It will not learn.

01:03:01.440 | It will stay constant, and it's just wasteful, but it doesn't actually really impact anything

01:03:06.200 | otherwise.

01:03:07.200 | Okay, so I rearranged the code a little bit with comments, and I just wanted to give a

01:03:10.640 | very quick summary of the batch normalization layer.

01:03:13.800 | We are using batch normalization to control the statistics of activations in the neural

01:03:18.600 | net.

01:03:19.600 | It is common to sprinkle batch normalization layer across the neural net, and usually we

01:03:23.880 | will place it after layers that have multiplications, like for example a linear layer or a convolutional

01:03:30.200 | layer, which we may cover in the future.

01:03:33.240 | Now the batch normalization internally has parameters for the gain and the bias, and

01:03:39.520 | these are trained using backpropagation.

01:03:41.820 | It also has two buffers.

01:03:44.460 | The buffers are the mean and the standard deviation, the running mean and the running

01:03:48.680 | mean of the standard deviation.

01:03:51.080 | And these are not trained using backpropagation.

01:03:53.040 | These are trained using this janky update of kind of like a running mean update.

01:03:59.000 | So these are sort of the parameters and the buffers of batch normalization layer.

01:04:05.320 | And then really what it's doing is it's calculating the mean and the standard deviation of the

01:04:09.040 | activations that are feeding into the batch normalization layer over that batch.

01:04:15.080 | Then it's centering that batch to be unit Gaussian, and then it's offsetting and scaling

01:04:20.040 | it by the learned bias and gain.

01:04:24.240 | And then on top of that, it's keeping track of the mean and standard deviation of the

01:04:27.640 | inputs, and it's maintaining this running mean and standard deviation.

01:04:32.920 | And this will later be used at inference so that we don't have to re-estimate the mean

01:04:36.920 | and standard deviation all the time.

01:04:39.200 | And in addition, that allows us to basically forward individual examples at test time.

01:04:43.520 | So that's the batch normalization layer.

01:04:45.960 | It's a fairly complicated layer, but this is what it's doing internally.

01:04:50.560 | Now I wanted to show you a little bit of a real example.

01:04:53.360 | So you can search ResNet, which is a residual neural network, and these are contacts of

01:04:59.120 | neural networks used for image classification.

01:05:02.320 | And of course, we haven't covered ResNets in detail, so I'm not going to explain all

01:05:06.520 | the pieces of it.

01:05:07.520 | But for now, just note that the image feeds into a ResNet on the top here, and there's

01:05:12.440 | many, many layers with repeating structure all the way to predictions of what's inside

01:05:16.880 | that image.

01:05:18.440 | This repeating structure is made up of these blocks, and these blocks are just sequentially

01:05:22.360 | stacked up in this deep neural network.

01:05:25.680 | Now the code for this, the block basically that's used and repeated sequentially in series,

01:05:32.480 | is called this bottleneck block.

01:05:36.360 | And there's a lot here.

01:05:37.480 | This is all PyTorch, and of course we haven't covered all of it, but I want to point out

01:05:40.960 | some small pieces of it.

01:05:43.320 | Here in the init is where we initialize the neural net.

01:05:45.760 | So this code of block here is basically the kind of stuff we're doing here.

01:05:49.040 | We're initializing all the layers.

01:05:51.200 | And in the forward, we are specifying how the neural net acts once you actually have

01:05:54.840 | the input.

01:05:55.840 | So this code here is along the lines of what we're doing here.

01:06:01.760 | And now these blocks are replicated and stacked up serially, and that's what a residual network

01:06:07.440 | would be.

01:06:09.040 | And so notice what's happening here.

01:06:11.160 | Conv1, these are convolution layers.

01:06:15.040 | And these convolution layers basically, they're the same thing as a linear layer, except convolution

01:06:20.340 | layers don't apply, convolution layers are used for images.

01:06:24.880 | And so they have spatial structure.

01:06:26.640 | And basically this linear multiplication and bias offset are done on patches instead of

01:06:32.480 | a map, instead of the full input.

01:06:34.840 | So because these images have structure, spatial structure, convolutions just basically do

01:06:39.520 | WX plus B, but they do it on overlapping patches of the input.

01:06:44.040 | But otherwise it's WX plus B.

01:06:46.920 | Then we have the normal layer, which by default here is initialized to be a batch norm in

01:06:50.800 | 2D, so two-dimensional batch normalization layer.

01:06:54.360 | And then we have a nonlinearity like ReLU.

01:06:56.780 | So instead of, here they use ReLU, we are using tanh in this case.

01:07:02.760 | But both are just nonlinearities and you can just use them relatively interchangeably.

01:07:07.440 | For very deep networks, ReLUs typically empirically work a bit better.

01:07:11.840 | So see the motif that's being repeated here.

01:07:14.200 | We have convolution, batch normalization, ReLU, convolution, batch normalization, ReLU,

01:07:18.800 | etc.

01:07:19.800 | And then here, this is a residual connection that we haven't covered yet.

01:07:23.120 | But basically that's the exact same pattern we have here.

01:07:25.480 | We have a weight layer, like a convolution or like a linear layer, batch normalization,

01:07:32.600 | and then tanh, which is nonlinearity.

01:07:35.680 | But basically a weight layer, a normalization layer, and nonlinearity.

01:07:39.700 | And that's the motif that you would be stacking up when you create these deep neural networks,

01:07:43.600 | exactly as is done here.

01:07:45.760 | And one more thing I'd like you to notice is that here when they are initializing the

01:07:49.280 | conv layers, like conv1x1, the depth for that is right here.

01:07:53.920 | And so it's initializing an nn.conv2d, which is a convolution layer in PyTorch.

01:07:59.160 | And there's a bunch of keyword arguments here that I'm not going to explain yet, but you

01:08:02.680 | see how there's bias equals false?

01:08:04.920 | The bias equals false is exactly for the same reason as bias is not used in our case.

01:08:10.240 | You see how I erased the use of bias?

01:08:12.320 | And the use of bias is spurious because after this weight layer, there's a batch normalization.

01:08:16.920 | And the batch normalization subtracts that bias and then has its own bias.

01:08:20.400 | So there's no need to introduce these spurious parameters.

01:08:23.280 | It wouldn't hurt performance, it's just useless.

01:08:25.960 | And so because they have this motif of conv, batch, and relu, they don't need a bias here

01:08:31.080 | because there's a bias inside here.

01:08:33.640 | So by the way, this example here is very easy to find.

01:08:37.120 | Just do ResNetPyTorch, and it's this example here.

01:08:41.920 | So this is kind of like the stock implementation of a residual neural network in PyTorch.

01:08:46.600 | And you can find that here.

01:08:48.320 | But of course, I haven't covered many of these parts yet.

01:08:50.840 | And I would also like to briefly descend into the definitions of these PyTorch layers and

01:08:55.400 | the parameters that they take.

01:08:57.120 | Now instead of a convolutional layer, we're going to look at a linear layer because that's

01:09:01.760 | the one that we're using here.

01:09:02.920 | This is a linear layer, and I haven't covered convolutions yet.

01:09:06.280 | But as I mentioned, convolutions are basically linear layers except on patches.

01:09:11.400 | So a linear layer performs a WX+B, except here they're calling the W a transpose.

01:09:18.920 | So it calculates WX+B very much like we did here.

01:09:21.620 | To initialize this layer, you need to know the fan in, the fan out, and that's so that

01:09:27.200 | they can initialize this W. This is the fan in and the fan out.

01:09:32.120 | So they know how big the weight matrix should be.

01:09:35.680 | You need to also pass in whether or not you want a bias.

01:09:39.240 | And if you set it to false, then no bias will be inside this layer.

01:09:44.600 | And you may want to do that exactly like in our case, if your layer is followed by a normalization

01:09:49.180 | layer such as batch norm.

01:09:51.900 | So this allows you to basically disable bias.

01:09:54.720 | In terms of the initialization, if we swing down here, this is reporting the variables

01:09:58.240 | used inside this linear layer.

01:10:01.200 | And our linear layer here has two parameters, the weight and the bias.

01:10:05.960 | In the same way, they have a weight and a bias.

01:10:08.840 | And they're talking about how they initialize it by default.

01:10:11.880 | So by default, PyTorch will initialize your weights by taking the fan in and then doing

01:10:18.120 | 1/fanin square root.

01:10:21.040 | And then instead of a normal distribution, they are using a uniform distribution.

01:10:25.900 | So it's very much the same thing, but they are using a 1 instead of 5/3, so there's no

01:10:30.940 | gain being calculated here.

01:10:32.640 | The gain is just 1.

01:10:33.860 | But otherwise, it's exactly 1/the square root of fanin, exactly as we have here.

01:10:40.600 | So 1/the square root of k is the scale of the weights.

01:10:45.440 | But when they are drawing the numbers, they're not using a Gaussian by default.

01:10:48.960 | They're using a uniform distribution by default.

01:10:51.600 | And so they draw uniformly from negative square root of k to square root of k.

01:10:56.080 | But it's the exact same thing and the same motivation with respect to what we've seen

01:11:01.360 | in this lecture.

01:11:03.260 | And the reason they're doing this is if you have a roughly Gaussian input, this will ensure

01:11:07.900 | that out of this layer, you will have a roughly Gaussian output.

01:11:12.020 | And you basically achieve that by scaling the weights by 1/the square root of fanin.

01:11:17.900 | So that's what this is doing.

01:11:20.260 | And then the second thing is the batch normalization layer.

01:11:23.340 | So let's look at what that looks like in PyTorch.

01:11:26.300 | So here we have a one-dimensional batch normalization layer, exactly as we are using here.

01:11:31.060 | And there are a number of keyword arguments going into it as well.

01:11:33.660 | So we need to know the number of features.

01:11:35.820 | For us, that is 200.

01:11:37.520 | And that is needed so that we can initialize these parameters here, the gain, the bias,

01:11:42.580 | and the buffers for the running mean and standard deviation.

01:11:47.140 | Then they need to know the value of epsilon here.

01:11:50.140 | And by default, this is 1.5.

01:11:51.820 | You don't typically change this too much.

01:11:54.080 | Then they need to know the momentum.

01:11:56.140 | And the momentum here, as they explain, is basically used for these running mean and

01:12:01.160 | running standard deviation.

01:12:02.900 | So by default, the momentum here is 0.1.

01:12:05.140 | The momentum we are using here in this example is 0.001.

01:12:09.940 | And basically, you may want to change this sometimes.

01:12:13.820 | And roughly speaking, if you have a very large batch size, then typically what you'll see

01:12:18.740 | is that when you estimate the mean and standard deviation for every single batch size, if

01:12:22.780 | it's large enough, you're going to get roughly the same result.

01:12:26.220 | And so therefore, you can use slightly higher momentum, like 0.1.

01:12:31.240 | But for a batch size as small as 32, the mean and standard deviation here might take on

01:12:36.700 | slightly different numbers, because there's only 32 examples we are using to estimate

01:12:40.460 | the mean and standard deviation.

01:12:41.960 | So the value is changing around a lot.

01:12:44.340 | And if your momentum is 0.1, that might not be good enough for this value to settle and

01:12:50.820 | converge to the actual mean and standard deviation over the entire training set.

01:12:55.260 | And so basically, if your batch size is very small, momentum of 0.1 is potentially dangerous,

01:12:59.920 | and it might make it so that the running mean and standard deviation is thrashing too much

01:13:04.380 | during training, and it's not actually converging properly.

01:13:09.740 | Affine equals true determines whether this batch normalization layer has these learnable

01:13:13.980 | affine parameters, the gain and the bias.

01:13:18.700 | And this is almost always kept to true.

01:13:20.700 | I'm not actually sure why you would want to change this to false.

01:13:26.620 | Then track running stats is determining whether or not batch normalization layer of PyTorch

01:13:30.780 | will be doing this.

01:13:33.060 | And one reason you may want to skip the running stats is because you may want to, for example,

01:13:39.540 | estimate them at the end as a stage two, like this.

01:13:42.860 | And in that case, you don't want the batch normalization layer to be doing all this extra

01:13:46.100 | compute that you're not going to use.

01:13:49.180 | And finally, we need to know which device we're going to run this batch normalization

01:13:52.940 | on, a CPU or a GPU, and what the data type should be, half precision, single precision,

01:13:58.220 | double precision, and so on.

01:14:01.220 | So that's the batch normalization layer.

01:14:02.580 | Otherwise, they link to the paper.

01:14:03.820 | It's the same formula we've implemented, and everything is the same, exactly as we've done

01:14:08.820 | here.

01:14:09.820 | Okay, so that's everything that I wanted to cover for this lecture.

01:14:14.020 | Really what I wanted to talk about is the importance of understanding the activations

01:14:17.260 | and the gradients and their statistics in neural networks.

01:14:20.720 | And this becomes increasingly important, especially as you make your neural networks bigger, larger,

01:14:24.460 | and deeper.

01:14:25.460 | We looked at the distributions basically at the output layer, and we saw that if you have

01:14:30.160 | two confident mispredictions because the activations are too messed up at the last layer, you can

01:14:35.260 | end up with these hockey stick losses.

01:14:37.780 | And if you fix this, you get a better loss at the end of training because your training

01:14:41.460 | is not doing wasteful work.

01:14:43.460 | Then we also saw that we need to control the activations.

01:14:46.060 | We don't want them to squash to zero or explode to infinity, because that you can run into

01:14:52.260 | a lot of trouble with all of these nonlinearities in these neural nets.

01:14:56.020 | And basically you want everything to be fairly homogeneous throughout the neural net.

01:14:58.980 | You want roughly Gaussian activations throughout the neural net.

01:15:02.620 | Then we talked about, okay, if we want roughly Gaussian activations, how do we scale these

01:15:07.780 | weight matrices and biases during initialization of the neural net so that we don't get, you

01:15:13.180 | know, so everything is as controlled as possible?

01:15:17.420 | So that gave us a large boost and improvement.

01:15:20.100 | And then I talked about how that strategy is not actually possible for much, much deeper

01:15:26.220 | neural nets, because when you have much deeper neural nets with lots of different types of

01:15:31.260 | layers, it becomes really, really hard to precisely set the weights and the biases in

01:15:36.460 | such a way that the activations are roughly uniform throughout the neural net.

01:15:41.420 | So then I introduced the notion of a normalization layer.

01:15:44.580 | Now there are many normalization layers that people use in practice.

01:15:48.020 | Batch normalization, layer normalization, instance normalization, group normalization.

01:15:52.740 | We haven't covered most of them, but I've introduced the first one and also the one

01:15:56.580 | that I believe came out first, and that's called batch normalization.

01:16:00.820 | And we saw how batch normalization works.

01:16:03.060 | This is a layer that you can sprinkle throughout your deep neural net.

01:16:06.540 | And the basic idea is if you want roughly Gaussian activations, well then take your

01:16:11.060 | activations and take the mean and the standard deviation and center your data.

01:16:16.740 | And you can do that because the centering operation is differentiable.

01:16:21.500 | But on top of that, we actually had to add a lot of bells and whistles, and that gave

01:16:25.620 | you a sense of the complexities of the batch normalization layer, because now we're centering

01:16:29.780 | the data, that's great, but suddenly we need the gain and the bias, and now those are trainable.

01:16:35.940 | And then because we are coupling all the training examples, now suddenly the question is how

01:16:39.740 | do you do the inference?

01:16:40.740 | Well, to do the inference, we need to now estimate these mean and standard deviation

01:16:47.300 | once over the entire training set, and then use those at inference.

01:16:51.980 | But then no one likes to do stage two, so instead we fold everything into the batch

01:16:56.140 | normalization layer during training and try to estimate these in a running manner so that

01:17:00.540 | everything is a bit simpler.

01:17:02.860 | And that gives us the batch normalization layer.

01:17:06.580 | And as I mentioned, no one likes this layer.

01:17:09.540 | It causes a huge amount of bugs.

01:17:12.740 | And intuitively it's because it is coupling examples in the forward pass of the neural

01:17:17.860 | net.

01:17:18.860 | And I've shot myself in the foot with this layer over and over again in my life, and

01:17:25.300 | I don't want you to suffer the same.

01:17:28.460 | So basically try to avoid it as much as possible.

01:17:32.140 | Some of the other alternatives to these layers are, for example, group normalization or layer

01:17:35.580 | normalization, and those have become more common in more recent deep learning, but we

01:17:41.420 | haven't covered those yet.

01:17:43.340 | But definitely batch normalization was very influential at the time when it came out in

01:17:46.900 | roughly 2015, because it was kind of the first time that you could train reliably much deeper

01:17:54.180 | neural nets.

01:17:55.460 | And fundamentally the reason for that is because this layer was very effective at controlling

01:17:59.780 | the statistics of the activations in the neural net.

01:18:03.260 | So that's the story so far.

01:18:05.580 | And that's all I wanted to cover.

01:18:08.000 | And in the future lectures, hopefully we can start going into recurrent neural nets.

01:18:11.860 | And recurrent neural nets, as we'll see, are just very, very deep networks, because you

01:18:17.460 | unroll the loop when you actually optimize these neural nets.

01:18:21.660 | And that's where a lot of this analysis around the activation statistics and all these normalization

01:18:28.620 | layers will become very, very important for good performance.

01:18:32.820 | So we'll see that next time.

01:18:33.820 | Bye.

01:18:34.820 | Okay, so I lied.

01:18:35.820 | I would like us to do one more summary here as a bonus.

01:18:39.420 | And I think it's useful as to have one more summary of everything I've presented in this

01:18:43.060 | lecture.

01:18:44.060 | But also I would like us to start PyTorchifying our code a little bit, so it looks much more

01:18:47.940 | like what you would encounter in PyTorch.

01:18:50.420 | So you'll see that I will structure our code into these modules, like a linear module and

01:18:57.060 | a batch form module.

01:18:58.740 | And I'm putting the code inside these modules so that we can construct neural networks very

01:19:02.920 | much like we would construct them in PyTorch.

01:19:04.820 | And I will go through this in detail.

01:19:06.780 | So we'll create our neural net.

01:19:08.940 | Then we will do the optimization loop, as we did before.

01:19:12.740 | And then the one more thing that I want to do here is I want to look at the activation

01:19:15.500 | statistics, both in the forward pass and in the backward pass.

01:19:19.460 | And then here we have the evaluation and sampling just like before.

01:19:23.060 | So let me rewind all the way up here and go a little bit slower.

01:19:26.920 | So here I am creating a linear layer.

01:19:29.420 | You'll notice that torch.nn has lots of different types of layers.

01:19:32.820 | And one of those layers is the linear layer.

01:19:34.700 | torch.nn.linear takes a number of input features, output features, whether or not we should

01:19:38.860 | have a bias, and then the device that we want to place this layer on, and the data type.

01:19:44.020 | So I will omit these two, but otherwise we have the exact same thing.

01:19:48.460 | We have the fan_in, which is the number of inputs, fan_out, the number of outputs, and

01:19:53.580 | whether or not we want to use a bias.

01:19:55.420 | And internally inside this layer, there's a weight and a bias, if you'd like it.

01:19:59.940 | It is typical to initialize the weight using, say, random numbers drawn from a Gaussian.

01:20:06.080 | And then here's the kyming initialization that we discussed already in this lecture.

01:20:10.720 | And that's a good default, and also the default that I believe PyTorch uses.

01:20:14.900 | And by default, the bias is usually initialized to zeros.

01:20:18.420 | Now when you call this module, this will basically calculate w times x plus b, if you have nb.

01:20:24.940 | And then when you also call .parameters on this module, it will return the tensors that

01:20:30.020 | are the parameters of this layer.

01:20:32.260 | Now next, we have the batch normalization layer.

01:20:34.620 | So I've written that here.

01:20:37.220 | And this is very similar to PyTorch's nn.batchnorm1d layer, as shown here.

01:20:44.500 | So I'm kind of taking these three parameters here, the dimensionality, the epsilon that

01:20:49.900 | we'll use in the division, and the momentum that we will use in keeping track of these

01:20:54.180 | running stats, the running mean and the running variance.

01:20:58.180 | Now PyTorch actually takes quite a few more things, but I'm assuming some of their settings.

01:21:02.340 | So for us, alphan will be true.

01:21:03.980 | That means that we will be using a gamma and beta after the normalization.

01:21:08.020 | The track running stats will be true, so we will be keeping track of the running mean

01:21:11.300 | and the running variance in the batch norm.

01:21:14.660 | Our device by default is the CPU, and the data type by default is float, float32.

01:21:22.260 | So those are the defaults.

01:21:23.660 | Otherwise, we are taking all the same parameters in this batch norm layer.

01:21:27.500 | So first, I'm just saving them.

01:21:29.980 | Now here's something new.

01:21:30.980 | There's a .training, which by default is true.

01:21:33.620 | And PyTorch nn modules also have this attribute, .training.

01:21:37.140 | And that's because many modules, and batch norm is included in that, have a different

01:21:42.100 | behavior whether you are training your neural net or whether you are running it in an evaluation

01:21:46.940 | mode and calculating your evaluation loss or using it for inference on some test examples.

01:21:53.060 | And batch norm is an example of this, because when we are training, we are going to be using

01:21:56.860 | the mean and the variance estimated from the current batch.

01:21:59.820 | But during inference, we are using the running mean and running variance.

01:22:04.140 | And so also, if we are training, we are updating mean and variance.

01:22:07.980 | But if we are testing, then these are not being updated.

01:22:10.100 | They're kept fixed.

01:22:11.880 | And so this flag is necessary and by default true, just like in PyTorch.

01:22:16.460 | Now the parameters of batch norm 1D are the gamma and the beta here.

01:22:21.940 | And then the running mean and the running variance are called buffers in PyTorch nomenclature.

01:22:27.780 | And these buffers are trained using exponential moving average here explicitly.

01:22:33.580 | And they are not part of the backpropagation and stochastic gradient descent.

01:22:37.100 | So they are not parameters of this layer.

01:22:39.960 | And that's why when we have parameters here, we only return gamma and beta.

01:22:44.700 | We do not return the mean and the variance.

01:22:46.740 | This is trained internally here, every forward pass, using exponential moving average.

01:22:54.700 | So that's the initialization.

01:22:55.700 | Now in a forward pass, if we are training, then we use the mean and the variance estimated

01:23:01.900 | by the batch.

01:23:02.900 | Let me pull up the paper here.

01:23:05.980 | We calculate the mean and the variance.

01:23:08.940 | Now up above, I was estimating the standard deviation and keeping track of the standard

01:23:13.260 | deviation here in the running standard deviation instead of running variance.

01:23:18.220 | But let's follow the paper exactly.

01:23:20.300 | Here they calculate the variance, which is the standard deviation squared.

01:23:24.000 | And that's what's kept track of in the running variance instead of the running standard deviation.

01:23:29.900 | But those two would be very, very similar, I believe.

01:23:33.980 | If we are not training, then we use the running mean and variance.

01:23:36.860 | We normalize.

01:23:39.180 | And then here, I'm calculating the output of this layer.

01:23:42.140 | And I'm also assigning it to an attribute called dot out.

01:23:45.540 | Now dot out is something that I'm using in our modules here.

01:23:49.660 | This is not what you would find in PyTorch.

01:23:51.420 | We are slightly deviating from it.

01:23:53.100 | I'm creating a dot out because I would like to very easily maintain all those variables

01:23:58.660 | so that we can create statistics of them and plot them.

01:24:01.500 | But PyTorch and modules will not have a dot out attribute.

01:24:05.500 | And finally here, we are updating the buffers using, again, as I mentioned, exponential

01:24:09.020 | moving average given the provided momentum.

01:24:13.100 | And importantly, you'll notice that I'm using the torch.nograd context manager.

01:24:17.420 | And I'm doing this because if we don't use this, then PyTorch will start building out

01:24:21.580 | an entire computational graph out of these tensors because it is expecting that we will

01:24:25.940 | eventually call dot backward.

01:24:28.120 | But we are never going to be calling dot backward on anything that includes running mean and

01:24:31.380 | running variance.

01:24:32.700 | So that's why we need to use this context manager so that we are not sort of maintaining

01:24:37.240 | and using all this additional memory.

01:24:40.500 | So this will make it more efficient.

01:24:41.620 | And it's just telling PyTorch that there will be no backward.

01:24:44.180 | We just have a bunch of tensors.

01:24:45.380 | We want to update them.

01:24:46.500 | That's it.

01:24:48.000 | And then we return.

01:24:49.340 | OK, now scrolling down, we have the 10H layer.

01:24:52.940 | This is very, very similar to torch.10H.

01:24:56.180 | And it doesn't do too much.

01:24:57.820 | It just calculates 10H, as you might expect.

01:25:00.580 | So that's torch.10H.

01:25:02.860 | And there's no parameters in this layer.

01:25:05.380 | But because these are layers, it now becomes very easy to sort of stack them up into basically

01:25:11.180 | just a list.

01:25:13.580 | And we can do all the initializations that we're used to.

01:25:16.400 | So we have the initial sort of embedding matrix.

01:25:19.580 | We have our layers.

01:25:20.580 | And we can call them sequentially.

01:25:22.380 | And then again, with torch.nograd, there's some initializations here.

01:25:26.260 | So we want to make the outputs of max a bit less confident, like we saw.

01:25:30.500 | And in addition to that, because we are using a six-layer multilayer perceptron here-- so

01:25:34.900 | you see how I'm stacking linear, 10H, linear, 10H, et cetera-- I'm going to be using the

01:25:40.200 | gain here.

01:25:41.460 | And I'm going to play with this in a second.

01:25:42.940 | So you'll see how when we change this, what happens to the statistics.

01:25:46.780 | Finally, the parameters are basically the embedding matrix and all the parameters in

01:25:51.300 | all the layers.

01:25:52.540 | And notice here, I'm using a double list comprehension, if you want to call it that.

01:25:56.220 | But for every layer in layers and for every parameter in each of those layers, we are

01:26:00.940 | just stacking up all those p's, all those parameters.

01:26:05.100 | Now in total, we have 46,000 parameters.

01:26:09.520 | And I'm telling PyTorch that all of them require gradient.

01:26:16.140 | Then here, we have everything here we are actually mostly used to.

01:26:20.780 | We are sampling batch.

01:26:22.140 | We are doing forward pass.

01:26:23.580 | The forward pass now is just a linear application of all the layers in order, followed by the

01:26:27.900 | cross entropy.

01:26:29.500 | And then in the backward pass, you'll notice that for every single layer, I now iterate

01:26:32.740 | over all the outputs.

01:26:34.220 | And I'm telling PyTorch to retain the gradient of them.

01:26:37.540 | And then here, we are already used to all the gradients set to none, do the backward

01:26:42.260 | to fill in the gradients, do an update using stochastic gradient send, and then track some

01:26:47.340 | statistics.

01:26:48.860 | And then I am going to break after a single iteration.

01:26:52.100 | Now here in this cell, in this diagram, I am visualizing the histograms of the forward

01:26:57.220 | pass activations.

01:26:58.780 | And I am specifically doing it at the 10-H layers.

01:27:01.920 | So iterating over all the layers, except for the very last one, which is basically just

01:27:06.260 | the softmax layer.

01:27:10.260 | If it is a 10-H layer, and I'm using a 10-H layer just because they have a finite output,

01:27:14.500 | negative one to one.

01:27:15.500 | And so it's very easy to visualize here.

01:27:17.180 | So you see negative one to one.

01:27:18.700 | And it's a finite range and easy to work with.

01:27:21.740 | I take the out tensor from that layer into T. And then I'm calculating the mean, the

01:27:27.020 | standard deviation, and the percent saturation of T. And the way I define the percent saturation

01:27:32.260 | is that T dot absolute value is greater than 0.97.

01:27:35.540 | So that means we are here at the tails of the 10-H. And remember that when we are in

01:27:39.660 | the tails of the 10-H, that will actually stop gradients.

01:27:42.920 | So we don't want this to be too high.

01:27:45.660 | Now here, I'm calling torch dot histogram.

01:27:49.180 | And then I am plotting this histogram.

01:27:51.300 | So basically what this is doing is that every different type of layer-- and they all have

01:27:54.340 | a different color-- we are looking at how many values in these tensors take on any of

01:28:00.860 | the values below on this axis here.

01:28:04.280 | So the first layer is fairly saturated here at 20%.

01:28:08.060 | So you can see that it's got tails here.

01:28:10.580 | But then everything sort of stabilizes.

01:28:12.620 | And if we had more layers here, it would actually just stabilize at around the standard deviation

01:28:15.980 | of about 0.65.

01:28:18.140 | And the saturation would be roughly 5%.

01:28:20.860 | And the reason that this stabilizes and gives us a nice distribution here is because gain

01:28:25.300 | is set to 5/3.

01:28:27.820 | Now here, this gain, you see that by default, we initialize with 1 over square root of fan

01:28:34.420 | in.

01:28:35.420 | But then here during initialization, I come in and I iterate over all the layers.

01:28:38.860 | And if it's a linear layer, I boost that by the gain.

01:28:42.500 | Now we saw that 1-- so basically, if we just do not use a gain, then what happens?

01:28:48.860 | If I redraw this, you will see that the standard deviation is shrinking and the saturation

01:28:55.340 | is coming to 0.

01:28:57.180 | And basically what's happening is the first layer is pretty decent.

01:29:01.060 | But then further layers are just kind of like shrinking down to 0.

01:29:05.060 | And it's happening slowly, but it's shrinking to 0.

01:29:07.760 | And the reason for that is when you just have a sandwich of linear layers alone, then initializing

01:29:15.880 | our weights in this manner we saw previously would have conserved the standard deviation

01:29:21.020 | of 1.

01:29:22.260 | But because we have this interspersed tanh layers in there, these tanh layers are squashing

01:29:28.620 | functions.

01:29:29.620 | And so they take your distribution and they slightly squash it.

01:29:33.020 | And so some gain is necessary to keep expanding it to fight the squashing.

01:29:40.080 | So it just turns out that 5/3 is a good value.

01:29:43.620 | So if we have something too small like 1, we saw that things will come towards 0.

01:29:49.140 | But if it's something too high, let's do 2.

01:29:52.540 | Then here we see that-- well, let me do something a bit more extreme so it's a bit more visible.

01:30:00.560 | Let's try 3.

01:30:01.560 | OK, so we see here that the saturations are starting to be way too large.

01:30:07.140 | So 3 would create way too saturated activations.

01:30:10.980 | So 5/3 is a good setting for a sandwich of linear layers with tanh activations.

01:30:17.940 | And it roughly stabilizes the standard deviation at a reasonable point.

01:30:22.060 | Now, honestly, I have no idea where 5/3 came from in PyTorch when we were looking at the

01:30:27.980 | counting initialization.

01:30:30.020 | I see empirically that it stabilizes this sandwich of linear and tanh and that the saturation

01:30:35.180 | is in a good range.

01:30:36.940 | But I don't actually know if this came out of some math formula.

01:30:39.500 | I tried searching briefly for where this comes from, but I wasn't able to find anything.

01:30:44.940 | But certainly we see that empirically these are very nice ranges.

01:30:47.460 | Our saturation is roughly 5%, which is a pretty good number.

01:30:51.100 | And this is a good setting of the gain in this context.

01:30:55.260 | Similarly, we can do the exact same thing with the gradients.

01:30:58.380 | So here is a very same loop if it's a tanh.

01:31:01.540 | But instead of taking the layer dot out, I'm taking the grad.

01:31:04.500 | And then I'm also showing the mean and the standard deviation.

01:31:07.340 | And I'm plotting the histogram of these values.

01:31:10.060 | And so you'll see that the gradient distribution is fairly reasonable.

01:31:13.640 | And in particular, what we're looking for is that all the different layers in this sandwich

01:31:17.700 | has roughly the same gradient.

01:31:19.700 | Things are not shrinking or exploding.

01:31:22.060 | So we can, for example, come here and we can take a look at what happens if this gain was

01:31:26.140 | way too small.

01:31:27.520 | So this was 0.5.

01:31:30.740 | Then you see the first of all, the activations are shrinking to zero, but also the gradients

01:31:35.140 | are doing something weird.

01:31:36.460 | The gradient started off here, and then now they're expanding out.

01:31:41.460 | And similarly, if we, for example, have a too high of a gain, so like 3, then we see

01:31:46.900 | that also the gradients have-- there's some asymmetry going on where as you go into deeper

01:31:50.900 | and deeper layers, the activations are also changing.

01:31:54.180 | And so that's not what we want.

01:31:55.540 | And in this case, we saw that without the use of BatchNorm, as we are going through

01:31:59.340 | right now, we have to very carefully set those gains to get nice activations in both the

01:32:05.580 | forward pass and the backward pass.

01:32:07.620 | Now before we move on to BatchNormalization, I would also like to take a look at what happens

01:32:11.900 | when we have no 10H units here.

01:32:14.040 | So erasing all the 10H nonlinearities, but keeping the gain at 5/3, we now have just

01:32:20.000 | a giant linear sandwich.

01:32:22.160 | So let's see what happens to the activations.

01:32:24.380 | As we saw before, the correct gain here is 1.

01:32:27.580 | That is the standard deviation preserving gain.

01:32:29.760 | So 1.667 is too high.

01:32:33.740 | And so what's going to happen now is the following.

01:32:37.020 | I have to change this to be linear, because there's no more 10H layers.

01:32:43.140 | And let me change this to linear as well.

01:32:46.140 | So what we're seeing is the activations started out on the blue and have, by layer four, become

01:32:54.140 | very diffuse.

01:32:55.220 | So what's happening to the activations is this.

01:32:57.980 | And with the gradients on the top layer, the activation, the gradient statistics are the

01:33:03.580 | purple, and then they diminish as you go down deeper in the layers.

01:33:07.740 | And so basically you have an asymmetry in the neural net.

01:33:10.980 | And you might imagine that if you have very deep neural networks, say like 50 layers or

01:33:13.960 | something like that, this is not a good place to be.

01:33:18.900 | So that's why before BatchNormalization, this was incredibly tricky to set.

01:33:24.260 | In particular, if this is too large of a gain, this happens, and if it's too little of a

01:33:28.060 | gain, then this happens.

01:33:31.540 | So the opposite of that basically happens.

01:33:33.580 | Here we have a shrinking and a diffusion, depending on which direction you look at it

01:33:40.980 | from.

01:33:41.980 | And so certainly this is not what you want.

01:33:44.260 | And in this case, the correct setting of the gain is exactly 1, just like we're doing at

01:33:49.100 | initialization.

01:33:50.300 | And then we see that the statistics for the forward and the backward paths are well-behaved.

01:33:56.300 | And so the reason I want to show you this is that basically getting neural nets to train

01:34:02.540 | before these normalization layers and before the use of advanced optimizers like Adam,

01:34:07.020 | which we still have to cover, and residual connections and so on, training neural nets

01:34:11.460 | basically looked like this.

01:34:12.460 | It's like a total balancing act.

01:34:15.020 | You have to make sure that everything is precisely orchestrated, and you have to care about the

01:34:18.940 | activations and the gradients and their statistics, and then maybe you can train something.

01:34:23.620 | But it was basically impossible to train very deep networks, and this is fundamentally the

01:34:26.900 | reason for that.

01:34:28.300 | You'd have to be very, very careful with your initialization.

01:34:32.300 | The other point here is, you might be asking yourself, by the way, I'm not sure if I covered

01:34:36.340 | this, why do we need these 10H layers at all?

01:34:40.860 | Why do we include them and then have to worry about the gain?

01:34:43.820 | And the reason for that, of course, is that if you just have a stack of linear layers,

01:34:47.980 | then certainly we're getting very easily nice activations and so on, but this is just a

01:34:53.300 | massive linear sandwich, and it turns out that it collapses to a single linear layer

01:34:57.260 | in terms of its representation power.

01:34:59.820 | So if you were to plot the output as a function of the input, you're just getting a linear

01:35:03.660 | function.

01:35:04.660 | No matter how many linear layers you stack up, you still just end up with a linear transformation.

01:35:09.100 | All the WX plus Bs just collapse into a large WX plus B with slightly different Ws and slightly

01:35:15.380 | different B.

01:35:16.380 | But interestingly, even though the forward pass collapses to just a linear layer, because

01:35:21.740 | of back propagation and the dynamics of the backward pass, the optimization actually is

01:35:27.140 | not identical.

01:35:28.700 | You actually end up with all kinds of interesting dynamics in the backward pass because of the

01:35:35.780 | way the chain rule is calculating it.

01:35:37.980 | And so optimizing a linear layer by itself and optimizing a sandwich of 10 linear layers,

01:35:43.920 | in both cases those are just a linear transformation in the forward pass, but the training dynamics

01:35:47.620 | would be different.

01:35:48.680 | And there's entire papers that analyze, in fact, infinitely layered linear layers and

01:35:53.660 | so on.

01:35:54.660 | And so there's a lot of things that you can play with there.

01:35:58.820 | But basically the 10-H nonlinearities allow us to turn this sandwich from just a linear

01:36:08.780 | chain into a neural network that can, in principle, approximate any arbitrary function.

01:36:14.820 | Okay, so now I've reset the code to use the linear 10-H sandwich like before, and I've

01:36:20.860 | reset everything so the gain is 5 over 3.

01:36:24.020 | We can run a single step of optimization and we can look at the activation statistics of

01:36:28.340 | the forward pass and the backward pass.

01:36:30.660 | But I've added one more plot here that I think is really important to look at when you're

01:36:33.900 | training your neural nets and to consider.

01:36:36.400 | And ultimately what we're doing is we're updating the parameters of the neural net.

01:36:40.240 | So we care about the parameters and their values and their gradients.

01:36:44.560 | So here what I'm doing is I'm actually iterating over all the parameters available and then

01:36:48.240 | I'm only restricting it to the two-dimensional parameters, which are basically the weights

01:36:53.360 | of these linear layers.

01:36:54.880 | And I'm skipping the biases and I'm skipping the gammas and the betas and the bastrom just

01:37:00.480 | for simplicity.

01:37:01.480 | But you can also take a look at those as well.

01:37:04.280 | But what's happening with the weights is instructive by itself.

01:37:09.080 | So here we have all the different weights, their shapes.

01:37:12.940 | So this is the embedding layer, the first linear layer, all the way to the very last

01:37:16.600 | linear layer.

01:37:17.600 | And then we have the mean, the standard deviation of all these parameters.

01:37:22.120 | The histogram, and you can see that it actually doesn't look that amazing, so there's some

01:37:25.320 | trouble in paradise.

01:37:26.860 | Even though these gradients looked okay, there's something weird going on here.

01:37:30.360 | I'll get to that in a second.

01:37:32.280 | And the last thing here is the gradient to data ratio.

01:37:36.000 | So sometimes I like to visualize this as well because what this gives you a sense of is

01:37:40.440 | what is the scale of the gradient compared to the scale of the actual values.

01:37:45.840 | And this is important because we're going to end up taking a step update that is the

01:37:51.000 | learning rate times the gradient onto the data.

01:37:54.280 | And so if the gradient has too large of a magnitude, if the numbers in there are too

01:37:57.680 | large compared to the numbers in data, then you'd be in trouble.

01:38:01.860 | But in this case, the gradient to data is our low numbers.

01:38:05.480 | So the values inside grad are 1000 times smaller than the values inside data in these weights,

01:38:12.600 | most of them.

01:38:14.000 | Now notably, that is not true about the last layer.

01:38:17.340 | And so the last layer actually here, the output layer, is a bit of a troublemaker in the way

01:38:20.920 | that this is currently arranged.

01:38:22.320 | Because you can see that the last layer here in pink takes on values that are much larger

01:38:30.720 | than some of the values inside the neural net.

01:38:36.020 | So the standard deviations are roughly 1 and -3 throughout, except for the last layer,

01:38:41.700 | which actually has roughly 1 and -2 standard deviation of gradients.

01:38:46.000 | And so the gradients on the last layer are currently about 100 times greater, sorry,

01:38:50.860 | 10 times greater than all the other weights inside the neural net.

01:38:56.020 | And so that's problematic because in the simple stochastic gradient descent setup, you would

01:39:00.560 | be training this last layer about 10 times faster than you would be training the other

01:39:04.820 | layers at initialization.

01:39:07.300 | Now this actually kind of fixes itself a little bit if you train for a bit longer.

01:39:11.240 | So for example, if I greater than 1000, only then do a break.

01:39:16.340 | Let me reinitialize, and then let me do it 1000 steps.

01:39:20.200 | And after 1000 steps, we can look at the forward pass.

01:39:24.460 | So you see how the neurons are saturating a bit.

01:39:27.940 | And we can also look at the backward pass.

01:39:30.180 | But otherwise they look good.

01:39:31.180 | They're about equal, and there's no shrinking to zero or exploding to infinities.

01:39:35.500 | And you can see that here in the weights, things are also stabilizing a little bit.

01:39:40.460 | So the tails of the last pink layer are actually coming in during the optimization.

01:39:46.460 | But certainly this is a little bit troubling, especially if you are using a very simple

01:39:50.420 | update rule like stochastic gradient descent instead of a modern optimizer like Atom.

01:39:55.380 | Now I'd like to show you one more plot that I usually look at when I train neural networks.

01:39:59.300 | And basically the gradient to data ratio is not actually that informative.

01:40:03.500 | Because what matters at the end is not the gradient to data ratio, but the update to

01:40:07.380 | the data ratio.

01:40:08.620 | Because that is the amount by which we will actually change the data in these tensors.

01:40:13.060 | So coming up here, what I'd like to do is I'd like to introduce a new update to data

01:40:17.420 | ratio.

01:40:18.420 | It's going to be a list, and we're going to build it out every single iteration.

01:40:23.300 | And here I'd like to keep track of basically the ratio every single iteration.

01:40:30.180 | So without any gradients, I'm comparing the update, which is learning rate times the gradient.

01:40:39.100 | That is the update that we're going to apply to every parameter.

01:40:42.740 | So see I'm iterating over all the parameters.

01:40:44.660 | And then I'm taking the basically standard deviation of the update we're going to apply

01:40:48.180 | and divide it by the actual content, the data of that parameter and its standard deviation.

01:40:56.220 | So this is the ratio of basically how great are the updates to the values in these tensors.

01:41:01.500 | Then we're going to take a log of it.

01:41:03.580 | And actually I'd like to take a log 10 just so it's a nicer visualization.

01:41:10.500 | So we're going to be basically looking at the exponents of this division here.

01:41:16.940 | And then that item to pop out the float.

01:41:19.460 | And we're going to be keeping track of this for all the parameters and adding it to this

01:41:22.460 | UD tensor.

01:41:24.300 | So now let me reinitialize and run a thousand iterations.

01:41:27.700 | We can look at the activations, the gradients, and the parameter gradients as we did before.

01:41:34.340 | But now I have one more plot here to introduce.

01:41:36.660 | And what's happening here is we're iterating over all the parameters, and I'm constraining

01:41:41.140 | it again like I did here to just the weights.

01:41:44.780 | So the number of dimensions in these sensors is two.

01:41:47.940 | And then I'm basically plotting all of these update ratios over time.

01:41:54.580 | So when I plot this, I plot those ratios and you can see that they evolve over time during

01:41:59.620 | initialization to take on certain values.

01:42:02.060 | And then these updates are like start stabilizing usually during training.

01:42:06.020 | Then the other thing that I'm plotting here is I'm plotting here like an approximate value

01:42:09.300 | that is a rough guide for what it roughly should be.

01:42:12.580 | And it should be like roughly 1 and -3.

01:42:15.580 | And so that means that basically there's some values in this tensor and they take on certain

01:42:20.980 | values and the updates to them at every single iteration are no more than roughly one thousandth

01:42:26.980 | of the actual magnitude in those tensors.

01:42:31.060 | If this was much larger, like for example, if the log of this was like say -1, this is

01:42:37.900 | actually updating those values quite a lot.

01:42:40.180 | They're undergoing a lot of change.

01:42:42.300 | But the reason that the final layer here is an outlier is because this layer was artificially

01:42:49.100 | shrunk down to keep the softmax unconfident.

01:42:54.580 | So here you see how we multiply the weight by 0.1 in the initialization to make the last

01:43:01.180 | layer prediction less confident.

01:43:04.380 | That artificially made the values inside that tensor way too low.

01:43:09.460 | And that's why we're getting temporarily a very high ratio.

01:43:12.260 | But you see that that stabilizes over time once that weight starts to learn.

01:43:18.100 | But basically I like to look at the evolution of this update ratio for all my parameters

01:43:22.420 | usually and I like to make sure that it's not too much above 1 and -3 roughly.

01:43:29.820 | So around -3 on this log plot.

01:43:33.160 | If it's below -3, usually that means that the parameters are not training fast enough.

01:43:37.520 | So if our learning rate was very low, let's do that experiment.

01:43:41.940 | Let's initialize and then let's actually do a learning rate of say 1 and -3 here.

01:43:47.620 | So 0.001.

01:43:49.700 | If your learning rate is way too low, this plot will typically reveal it.

01:43:56.500 | So you see how all of these updates are way too small.

01:44:00.460 | So the size of the update is basically 10,000 times in magnitude to the size of the numbers

01:44:09.080 | in that tensor in the first place.

01:44:10.740 | So this is a symptom of training way too slow.

01:44:14.700 | So this is another way to sometimes set the learning rate and to get a sense of what that

01:44:17.720 | learning rate should be.

01:44:19.280 | And ultimately this is something that you would keep track of.

01:44:25.120 | If anything, the learning rate here is a little bit on the higher side because you see that

01:44:31.920 | we're above the black line of -3.

01:44:34.020 | We're somewhere around -2.5.

01:44:36.080 | It's like okay.

01:44:37.960 | But everything is somewhat stabilizing and so this looks like a pretty decent setting

01:44:41.340 | of learning rates and so on.

01:44:43.680 | But this is something to look at.

01:44:45.160 | And when things are miscalibrated, you will see very quickly.

01:44:48.520 | So for example, everything looks pretty well behaved, right?

01:44:52.380 | But just as a comparison, when things are not properly calibrated, what does that look

01:44:55.500 | like?

01:44:56.580 | Let me come up here and let's say that for example, what do we do?

01:45:01.920 | Let's say that we forgot to apply this fan-in normalization.

01:45:05.900 | So the weights inside the linear layers are just a sample from a Gaussian in all those

01:45:10.180 | stages.

01:45:11.180 | What happens to our - how do we notice that something's off?

01:45:14.620 | Well the activation plot will tell you, whoa, your neurons are way too saturated.

01:45:18.940 | The gradients are going to be all messed up.

01:45:21.460 | And the histogram for these weights are going to be all messed up as well.

01:45:25.420 | And there's a lot of asymmetry.

01:45:27.260 | And then if we look here, I suspect it's all going to be also pretty messed up.

01:45:30.780 | So you see there's a lot of discrepancy in how fast these layers are learning.

01:45:36.540 | And some of them are learning way too fast.

01:45:38.700 | So -1, -1.5, those are very large numbers in terms of this ratio.

01:45:43.780 | Again, you should be somewhere around -3 and not much more above that.

01:45:48.640 | So this is how miscalibrations of your neural nets are going to manifest.

01:45:53.020 | And these kinds of plots here are a good way of sort of bringing those miscalibrations

01:46:01.820 | to your attention and so you can address them.

01:46:04.100 | Okay, so so far we've seen that when we have this linear tanh sandwich, we can actually

01:46:08.780 | precisely calibrate the gains and make the activations, the gradients, and the parameters,

01:46:13.460 | and the updates all look pretty decent.

01:46:15.960 | But it definitely feels a little bit like balancing of a pencil on your finger.

01:46:21.340 | And that's because this gain has to be very precisely calibrated.

01:46:26.040 | So now let's introduce batch normalization layers into the mix.

01:46:30.720 | Let's see how that helps fix the problem.

01:46:34.020 | So here, I'm going to take the BatchNorm1D class, and I'm going to start placing it inside.

01:46:41.220 | And as I mentioned before, the standard typical place you would place it is between the linear

01:46:46.780 | layer, so right after it, but before the nonlinearity.

01:46:49.320 | But people have definitely played with that.

01:46:51.480 | And in fact, you can get very similar results, even if you place it after the nonlinearity.

01:46:57.960 | And the other thing that I wanted to mention is it's totally fine to also place it at the

01:47:00.960 | end, after the last linear layer and before the loss function.

01:47:04.880 | So this is potentially fine as well.

01:47:08.940 | And in this case, this would be output, would be vocab size.

01:47:14.260 | Now because the last layer is BatchNorm, we would not be changing the weight to make the

01:47:19.200 | softmax less confident.

01:47:20.720 | We'd be changing the gamma.

01:47:23.240 | Because gamma, remember, in the BatchNorm, is the variable that multiplicatively interacts

01:47:28.120 | with the output of that normalization.

01:47:32.800 | So we can initialize this sandwich now.

01:47:35.920 | We can train, and we can see that the activations are going to of course look very good.

01:47:41.920 | And they are going to necessarily look good, because now before every single tanh layer,

01:47:46.920 | there is a normalization in the BatchNorm.

01:47:49.380 | So this is unsurprisingly all looks pretty good.

01:47:53.080 | It's going to be standard deviation of roughly 0.65, 2%, and roughly equal standard deviation

01:47:58.120 | throughout the entire layers.

01:47:59.840 | So everything looks very homogeneous.

01:48:02.800 | The gradients look good.

01:48:04.800 | The weights look good in their distributions.

01:48:09.400 | And then the updates also look pretty reasonable.

01:48:14.360 | We're going above -3 a little bit, but not by too much.

01:48:18.020 | So all the parameters are training at roughly the same rate here.

01:48:24.840 | But now what we've gained is we are going to be slightly less brittle with respect to

01:48:32.800 | the gain of these.

01:48:34.300 | So for example, I can make the gain be, say, 0.2 here, which is much slower than what we

01:48:40.760 | had with the tanh.

01:48:43.120 | But as we'll see, the activations will actually be exactly unaffected.

01:48:47.000 | And that's because of, again, this explicit normalization.

01:48:49.780 | The gradients are going to look okay.

01:48:51.520 | The weight gradients are going to look okay.

01:48:54.120 | But actually the updates will change.

01:48:57.100 | And so even though the forward and backward paths to a very large extent look okay, because

01:49:01.920 | of the backward paths of the Bash norm and how the scale of the incoming activations

01:49:06.040 | interacts in the Bash norm and its backward paths, this is actually changing the scale

01:49:13.960 | of the updates on these parameters.

01:49:16.420 | So the gradients of these weights are affected.

01:49:19.760 | So we still don't get a completely free path to pass in arbitrary weights here, but everything

01:49:26.500 | else is significantly more robust in terms of the forward, backward, and the weight gradients.

01:49:33.160 | It's just that you may have to retune your learning rate if you are changing sufficiently

01:49:37.460 | the scale of the activations that are coming into the Bash norms.

01:49:41.620 | So here, for example, we changed the gains of these linear layers to be greater, and

01:49:47.380 | we're seeing that the updates are coming out lower as a result.

01:49:51.880 | And then finally, if we are using Bash norms, we don't actually need to necessarily—let

01:49:56.280 | me reset this to 1 so there's no gain—we don't necessarily even have to normalize

01:50:02.080 | backfan_in sometimes.

01:50:03.640 | So if I take out the fan_in, so these are just now random Gaussian, we'll see that

01:50:08.640 | because of Bash norm, this will actually be relatively well-behaved.

01:50:11.920 | So this will of course in the forward path look good.

01:50:17.680 | The gradients look good.

01:50:20.000 | The backward weight updates look okay.

01:50:23.720 | A little bit of fat tails on some of the layers, and this looks okay as well.

01:50:29.040 | But as you can see, we're significantly below -3, so we'd have to bump up the learning

01:50:35.000 | rate of this Bash norm so that we are training more properly.

01:50:38.760 | And in particular, looking at this, roughly looks like we have to 10x the learning rate

01:50:43.240 | to get to about 1e-3.

01:50:46.860 | So we'd come here and we would change this to be update of 1.0.

01:50:51.520 | And if I reinitialize, then we'll see that everything still of course looks good.

01:51:02.600 | And now we are roughly here, and we expect this to be an okay training run.

01:51:07.280 | So long story short, we are significantly more robust to the gain of these linear layers,

01:51:11.840 | whether or not we have to apply the fan_in.

01:51:14.240 | And then we can change the gain, but we actually do have to worry a little bit about the update

01:51:20.040 | scales and making sure that the learning rate is properly calibrated here.

01:51:24.320 | But the activations of the forward, backward paths and the updates are looking significantly

01:51:29.120 | more well-behaved, except for the global scale that is potentially being adjusted here.

01:51:33.760 | Okay, so now let me summarize.

01:51:36.660 | There are three things I was hoping to achieve with this section.

01:51:39.640 | Number one, I wanted to introduce you to Bash normalization, which is one of the first modern

01:51:43.840 | innovations that we're looking into that helped stabilize very deep neural networks and their

01:51:48.600 | training.

01:51:50.000 | And I hope you understand how the Bash normalization works and how it would be used in a neural

01:51:54.920 | network.

01:51:56.280 | Number two, I was hoping to PyTorchify some of our code and wrap it up into these modules.

01:52:01.960 | So like linear, Bash normalization 1D, 10H, et cetera.

01:52:04.800 | These are layers or modules, and they can be stacked up into neural nets like Lego building

01:52:09.800 | blocks.

01:52:11.160 | And these layers actually exist in PyTorch.

01:52:15.080 | And if you import torch-nn, then you can actually, the way I've constructed it, you can simply

01:52:19.800 | just use PyTorch by prepending nn. to all these different layers.

01:52:25.440 | And actually everything will just work because the API that I've developed here is identical

01:52:30.460 | to the API that PyTorch uses.

01:52:32.880 | And the implementation also is basically, as far as I'm aware, identical to the one

01:52:36.920 | in PyTorch.

01:52:37.920 | And number three, I tried to introduce you to the diagnostic tools that you would use

01:52:42.440 | to understand whether your neural network is in a good state dynamically.

01:52:46.420 | So we are looking at the statistics and histograms and activation of the forward pass activations,

01:52:52.320 | the backward pass gradients.

01:52:54.200 | And then also we're looking at the weights that are going to be updated as part of stochastic

01:52:57.920 | gradient ascent.

01:52:59.120 | And we're looking at their means, standard deviations, and also the ratio of gradients

01:53:03.520 | to data, or even better, the updates to data.

01:53:08.040 | And we saw that typically we don't actually look at it as a single snapshot frozen in

01:53:11.680 | time at some particular iteration.

01:53:14.080 | Typically people look at this as over time, just like I've done here.

01:53:17.900 | And they look at these update to data ratios and they make sure everything looks okay.

01:53:21.680 | And in particular, I said that 1e-3, or basically negative 3 on the log scale, is a good rough

01:53:29.120 | heuristic for what you want this ratio to be.

01:53:31.920 | And if it's way too high, then probably the learning rate or the updates are a little

01:53:35.560 | too big.

01:53:36.560 | And if it's way too small, then the learning rate is probably too small.

01:53:39.840 | So that's just some of the things that you may want to play with when you try to get

01:53:43.080 | your neural network to work very well.

01:53:45.960 | Now, there's a number of things I did not try to achieve.

01:53:49.200 | I did not try to beat our previous performance, as an example, by introducing the BatchNorm

01:53:53.080 | layer.

01:53:54.080 | Actually, I did try, and I found that I used the learning rate finding mechanism that I've

01:53:58.840 | described before.

01:53:59.840 | I tried to train the BatchNorm layer, a BatchNorm neural net, and I actually ended up with results

01:54:05.400 | that are very, very similar to what we've obtained before.

01:54:08.440 | And that's because our performance now is not bottlenecked by the optimization, which

01:54:13.120 | is what BatchNorm is helping with.

01:54:15.220 | The performance at this stage is bottlenecked by what I suspect is the context length of

01:54:20.080 | our context.

01:54:22.080 | So currently, we are taking three characters to predict the fourth one, and I think we

01:54:25.140 | need to go beyond that.

01:54:26.240 | And we need to look at more powerful architectures, like recurrent neural networks and transformers,

01:54:31.000 | in order to further push the like probabilities that we're achieving on this dataset.

01:54:36.840 | And I also did not try to have a full explanation of all of these activations, the gradients

01:54:42.400 | and the backward pass, and the statistics of all these gradients.

01:54:45.640 | And so you may have found some of the parts here unintuitive, and maybe you're slightly

01:54:48.640 | confused about, okay, if I change the gain here, how come that we need a different learning

01:54:53.600 | rate?

01:54:54.600 | But I didn't go into the full detail, because you'd have to actually look at the backward

01:54:57.120 | pass of all these different layers and get an intuitive understanding of how that works.

01:55:01.480 | And I did not go into that in this lecture.

01:55:04.040 | The purpose really was just to introduce you to the diagnostic tools and what they look

01:55:07.560 | like.

01:55:08.560 | But there's still a lot of work remaining on the intuitive level to understand the initialization,

01:55:12.720 | the backward pass, and how all of that interacts.

01:55:15.880 | But you shouldn't feel too bad, because honestly, we are getting to the cutting edge of where

01:55:21.480 | the field is.

01:55:22.960 | We certainly haven't, I would say, solved initialization, and we haven't solved backpropagation.

01:55:28.360 | And these are still very much an active area of research.

01:55:30.960 | People are still trying to figure out what is the best way to initialize these networks,

01:55:33.960 | what is the best update rule to use, and so on.

01:55:37.440 | So none of this is really solved, and we don't really have all the answers to all these cases.

01:55:44.240 | But at least we're making progress, and at least we have some tools to tell us whether

01:55:48.440 | or not things are on the right track for now.

01:55:51.800 | So I think we've made positive progress in this lecture, and I hope you enjoyed that.

01:55:56.120 | And I will see you next time.

Building makemore Part 3: Activations & Gradients, BatchNorm

Chapters