Hi everyone. Today we are continuing our implementation of Makemore. Now in the last lecture we implemented the multilayer perceptron along the lines of Benji Hotel 2003 for character level language modeling. So we followed this paper, took in a few characters in the past, and used an MLP to predict the next character in a sequence.

So what we'd like to do now is we'd like to move on to more complex and larger neural networks, like recurrent neural networks and their variations like the GRU, LSTM, and so on. Now, before we do that though, we have to stick around the level of multilayer perceptron for a bit longer.

And I'd like to do this because I would like us to have a very good intuitive understanding of the activations in the neural net during training, and especially the gradients that are flowing backwards, and how they behave and what they look like. This is going to be very important to understand the history of the development of these architectures, because we'll see that recurrent neural networks, while they are very expressive in that they are a universal approximator and can in principle implement all the algorithms, we'll see that they are not very easily optimizable with the first-order gradient-based techniques that we have available to us and that we use all the time.

And the key to understanding why they are not optimizable easily is to understand the activations and the gradients and how they behave during training. And we'll see that a lot of the variants since recurrent neural networks have tried to improve that situation. And so that's the path that we have to take, and let's get started.

So the starting code for this lecture is largely the code from before, but I've cleaned it up a little bit. So you'll see that we are importing all the Torch and Mathplotlib utilities. We're reading in the words just like before. These are eight example words. There's a total of 32,000 of them.

Here's a vocabulary of all the lowercase letters and the special dot token. Here we are reading the dataset and processing it and creating three splits, the train, dev, and the test split. Now in the MLP, this is the identical same MLP, except you see that I removed a bunch of magic numbers that we had here.

And instead we have the dimensionality of the embedding space of the characters and the number of hidden units in the hidden layer. And so I've pulled them outside here so that we don't have to go and change all these magic numbers all the time. With the same neural net with 11,000 parameters that we optimize now over 200,000 steps with a batch size of 32.

And you'll see that I refactored the code here a little bit, but there are no functional changes. I just created a few extra variables, a few more comments, and I removed all the magic numbers. And otherwise it's the exact same thing. Then when we optimize, we saw that our loss looked something like this.

We saw that the train and val loss were about 2.16 and so on. Here I refactored the code a little bit for the evaluation of arbitrary splits. So you pass in a string of which split you'd like to evaluate. And then here, depending on train, val, or test, I index in and I get the correct split.

And then this is the forward pass of the network and evaluation of the loss and printing it. So just making it nicer. One thing that you'll notice here is I'm using a decorator torch.nograd, which you can also look up and read documentation of. Basically what this decorator does on top of a function is that whatever happens in this function is assumed by Torch to never require any gradients.

So it will not do any of the bookkeeping that it does to keep track of all the gradients in anticipation of an eventual backward pass. It's almost as if all the tensors that get created here have a requires grad of false. And so it just makes everything much more efficient because you're telling Torch that I will not call .backward on any of this computation and you don't need to maintain the graph under the hood.

So that's what this does. And you can also use a context manager with torch.nograd and you can look those up. Then here we have the sampling from a model just as before. So for passive neural net, getting the distribution, sampling from it, adjusting the context window and repeating until we get the special end token.

And we see that we are starting to get much nicer looking words sampled from the model. It's still not amazing and they're still not fully name-like, but it's much better than when we had to do it with the bigram model. So that's our starting point. Now the first thing I would like to scrutinize is the initialization.

I can tell that our network is very improperly configured at initialization and there's multiple things wrong with it, but let's just start with the first one. Look here on the zeroth iteration, the very first iteration, we are recording a loss of 27 and this rapidly comes down to roughly one or two or so.

So I can tell that the initialization is all messed up because this is way too high. In training of neural nets, it is almost always the case that you will have a rough idea for what loss to expect at initialization, and that just depends on the loss function and the problem setup.

In this case, I do not expect 27. I expect a much lower number and we can calculate it together. Basically at initialization, what we'd like is that there's 27 characters that could come next for any one training example. At initialization, we have no reason to believe any characters to be much more likely than others.

And so we'd expect that the probability distribution that comes out initially is a uniform distribution assigning about equal probability to all the 27 characters. So basically what we'd like is the probability for any character would be roughly one over 27. That is the probability we should record. And then the loss is the negative log probability.

So let's wrap this in a tensor and then that one can take the log of it. And then the negative log probability is the loss we would expect, which is 3.29, much, much lower than 27. And so what's happening right now is that at initialization, the neural net is creating probability distributions that are all messed up.

Some characters are very confident and some characters are very not confident. And then basically what's happening is that the network is very confidently wrong and that's what makes it record very high loss. So here's a smaller four-dimensional example of the issue. Let's say we only have four characters and then we have logits that come out of the neural net and they are very, very close to zero.

Then when we take the softmax of all zeros, we get probabilities that are a diffuse distribution. So sums to one and is exactly uniform. And then in this case, if the label is say two, it doesn't actually matter if the label is two or three or one or zero because it's a uniform distribution.

We're recording the exact same loss in this case, 1.38. So this is the loss we would expect for a four-dimensional example. And I can see of course that as we start to manipulate these logits, we're going to be changing the loss here. So it could be that we luck out and by chance this could be a very high number like five or something like that.

Then in that case, we'll record a very low loss because we're assigning the correct probability at initialization by chance to the correct label. Much more likely it is that some other dimension will have a high logit. And then what will happen is we start to record a much higher loss.

And what can happen is basically the logits come out like something like this, and they take on extreme values and we record really high loss. For example, if we have torq.random of four. So these are normally distributed numbers, four of them. Then here we can also print the logits, probabilities that come out of it and loss.

And so because these logits are near zero, for the most part, the loss that comes out is okay. But suppose this is like times 10 now. You see how because these are more extreme values, it's very unlikely that you're going to be guessing the correct bucket and then you're confidently wrong and recording very high loss.

If your logits are coming out even more extreme, you might get extremely insane losses like infinity even at initialization. So basically this is not good and we want the logits to be roughly zero when the network is initialized. In fact, the logits don't have to be just zero, they just have to be equal.

So for example, if all the logits are one, then because of the normalization inside the softmax, this will actually come out okay. But by symmetry, we don't want it to be any arbitrary positive or negative number. We just want it to be all zeros and record the loss that we expect at initialization.

So let's now concretely see where things go wrong in our example. Here we have the initialization. Let me reinitialize the neural net. And here let me break after the very first iteration so we only see the initial loss, which is 27. So that's way too high. And intuitively now we can expect the variables involved and we see that the logits here, if we just print some of these, if we just print the first row, we see that the logits take on quite extreme values.

And that's what's creating the fake confidence in incorrect answers and makes the loss get very, very high. So these logits should be much, much closer to zero. So now let's think through how we can achieve logits coming out of this neural net to be more closer to zero. You see here that logits are calculated as the hidden states multiplied by W2 plus B2.

So first of all, currently we're initializing B2 as random values of the right size. But because we want roughly zero, we don't actually want to be adding a bias of random numbers. So I'm going to add a times a zero here to make sure that B2 is just basically zero at initialization.

And second, this is H multiplied by W2. So if we want logits to be very, very small, then we would be multiplying W2 and making that smaller. So for example, if we scale down W2 by 0.1, all the elements, then if I do again just the very first iteration, you see that we are getting much closer to what we expect.

So roughly what we want is about 3.29. This is 4.2. I can make this maybe even smaller. 3.32. Okay, so we're getting closer and closer. Now you're probably wondering, can we just set this to zero? Then we get, of course, exactly what we're looking for at initialization. And the reason I don't usually do this is because I'm very nervous, and I'll show you in a second why you don't want to be setting W's or weights of a neural net exactly to zero.

You usually want it to be small numbers instead of exactly zero. For this output layer in this specific case, I think it would be fine, but I'll show you in a second where things go wrong very quickly if you do that. So let's just go with 0.01. In that case, our loss is close enough, but has some entropy.

It's not exactly zero. It's got some little entropy, and that's used for symmetry breaking, as we'll see in a second. The logits are now coming out much closer to zero, and everything is well and good. So if I just erase these, and I now take away the break statement, we can run the optimization with this new initialization.

And let's just see what losses we record. Okay, so I let it run, and you see that we started off good, and then we came down a bit. The plot of the loss now doesn't have this hockey-shape appearance, because basically what's happening in the hockey stick, the very first few iterations of the loss, what's happening during the optimization is the optimization is just squashing down the logits, and then it's rearranging the logits.

So basically, we took away this easy part of the loss function where just the weights were just being shrunk down. And so therefore, we don't get these easy gains in the beginning, and we're just getting some of the hard gains of training the actual neural net, and so there's no hockey stick appearance.

So good things are happening in that both, number one, loss at initialization is what we expect, and the loss doesn't look like a hockey stick. And this is true for any neural net you might train, and something to look out for. And second, the loss that came out is actually quite a bit improved.

Unfortunately, I erased what we had here before. I believe this was 2.12, and this was 2.16. So we get a slightly improved result, and the reason for that is because we're spending more cycles, more time, optimizing the neural net actually, instead of just spending the first several thousand iterations probably just squashing down the weights, because they are so way too high in the beginning of the initialization.

So something to look out for, and that's number one. Now let's look at the second problem. Let me reinitialize our neural net, and let me reintroduce the break statement, so we have a reasonable initial loss. So even though everything is looking good on the level of the loss, and we get something that we expect, there's still a deeper problem lurking inside this neural net and its initialization.

So the logits are now okay. The problem now is with the values of h, the activations of the hidden states. Now if we just visualize this vector, sorry, this tensor h, it's kind of hard to see, but the problem here, roughly speaking, is you see how many of the elements are 1 or -1?

Now recall that torch.10h, the 10h function, is a squashing function. It takes arbitrary numbers and it squashes them into a range of -1 and 1, and it does so smoothly. So let's look at the histogram of h to get a better idea of the distribution of the values inside this tensor.

We can do this first. Well we can see that h is 32 examples and 200 activations in each example. We can view it as -1, stretch it out into one large vector, and we can then call toList to convert this into one large Python list of floats. And then we can pass this into plt.hist for histogram, and we say we want 50 bins, and a semicolon to suppress a bunch of output we don't want.

So we see this histogram, and we see that most of the values by far take on value of -1 and 1. So this 10h is very, very active. And we can also look at basically why that is. We can look at the preactivations that feed into the 10h, and we can see that the distribution of the preactivations is very, very broad.

These take numbers between -15 and 15, and that's why in a torch.10h everything is being squashed and capped to be in the range of -1 and 1, and lots of numbers here take on very extreme values. Now if you are new to neural networks, you might not actually see this as an issue.

But if you're well-versed in the dark arts of backpropagation and have an intuitive sense of how these gradients flow through a neural net, you are looking at your distribution of 10h activations here, and you are sweating. So let me show you why. We have to keep in mind that during backpropagation, just like we saw in micrograd, we are doing backward pass starting at the loss and flowing through the network backwards.

In particular, we're going to backpropagate through this torch.10h. And this layer here is made up of 200 neurons for each one of these examples, and it implements an element-wise 10h. So let's look at what happens in 10h in the backward pass. We can actually go back to our previous micrograd code in the very first lecture and see how we implemented 10h.

We saw that the input here was x, and then we calculate t, which is the 10h of x. So that's t. And t is between -1 and 1. It's the output of the 10h. And then in the backward pass, how do we backpropagate through a 10h? We take out.grad, and then we multiply it, this is the chain rule, with the local gradient, which took the form of 1 - t^2.

So what happens if the outputs of your 10h are very close to -1 or 1? If you plug in t = 1 here, you're going to get a 0, multiplying out.grad. No matter what out.grad is, we are killing the gradient, and we're stopping, effectively, the backpropagation through this 10h unit.

Similarly, when t is -1, this will again become 0, and out.grad just stops. And intuitively, this makes sense, because this is a 10h neuron, and what's happening is if its output is very close to 1, then we are in the tail of this 10h. And so changing, basically, the input is not going to impact the output of the 10h too much, because it's in a flat region of the 10h.

And so therefore, there's no impact on the loss. And so indeed, the weights and the biases along with this 10h neuron do not impact the loss, because the output of this 10h unit is in the flat region of the 10h, and there's no influence. We can be changing them however we want, and the loss is not impacted.

That's another way to justify that, indeed, the gradient would be basically 0. It vanishes. Indeed, when t equals 0, we get 1 times out.grad. So when the 10h takes on exactly value of 0, then out.grad is just passed through. So basically what this is doing is if t is equal to 0, then the 10h unit is inactive, and a gradient just passes through.

But the more you are in the flat tails, the more the gradient is squashed. So in fact, you'll see that the gradient flowing through 10h can only ever decrease, and the amount that it decreases is proportional through a square here, depending on how far you are in the flat tails of this 10h.

And so that's kind of what's happening here. And the concern here is that if all of these outputs h are in the flat regions of negative 1 and 1, then the gradients that are flowing through the network will just get destroyed at this layer. Now there is some redeeming quality here, and that we can actually get a sense of the problem here as follows.

I wrote some code here. Basically what we want to do here is we want to take a look at h, take the absolute value, and see how often it is in the flat region, so say greater than 0.99. And what you get is the following. And this is a Boolean tensor.

So in the Boolean tensor, you get a white if this is true and a black if this is false. And so basically what we have here is the 32 examples and the 200 hidden neurons. And we see that a lot of this is white. And what that's telling us is that all these 10h neurons were very, very active, and they're in the flat tail.

And so in all these cases, the backward gradient would get destroyed. Now we would be in a lot of trouble if for any one of these 200 neurons, if it was the case that the entire column is white, because in that case, we have what's called a dead neuron.

And this could be a 10h neuron where the initialization of the weights and the biases could be such that no single example ever activates this 10h in the sort of active part of the 10h. If all the examples land in the tail, then this neuron will never learn. It is a dead neuron.

And so just scrutinizing this and looking for columns of completely white, we see that this is not the case. So I don't see a single neuron that is all of white. And so therefore, it is the case that for every one of these 10h neurons, we do have some examples that activate them in the active part of the 10h.

And so some gradients will flow through, and this neuron will learn. And the neuron will change, and it will move, and it will do something. But you can sometimes get yourself in cases where you have dead neurons. And the way this manifests is that for a 10h neuron, this would be when no matter what inputs you plug in from your data set, this 10h neuron always fires completely one or completely negative one.

And then it will just not learn, because all the gradients will be just zeroed out. This is true not just for 10h, but for a lot of other nonlinearities that people use in neural networks. So we certainly use 10h a lot, but sigmoid will have the exact same issue, because it is a squashing neuron.

And so the same will be true for sigmoid, but basically the same will actually apply to sigmoid. The same will also apply to a ReLU. So ReLU has a completely flat region here below zero. So if you have a ReLU neuron, then it is a pass-through if it is positive.

And if the pre-activation is negative, it will just shut it off. Since the region here is completely flat, then during backpropagation, this would be exactly zeroing out the gradient. All of the gradient would be set exactly to zero instead of just a very, very small number depending on how positive or negative t is.

And so you can get, for example, a dead ReLU neuron. And a dead ReLU neuron would basically look like-- basically what it is is if a neuron with a ReLU nonlinearity never activates. So for any examples that you plug in in the dataset, it never turns on. It's always in this flat region.

Then this ReLU neuron is a dead neuron. Its weights and bias will never learn. They will never get a gradient because the neuron never activated. And this can sometimes happen at initialization because the weights and the biases just make it so that by chance some neurons are just forever dead.

But it can also happen during optimization. If you have like a too high of a learning rate, for example, sometimes you have these neurons that get too much of a gradient and they get knocked out of the data manifold. And what happens is that from then on, no example ever activates this neuron.

So this neuron remains dead forever. So it's kind of like a permanent brain damage in a mind of a network. And so sometimes what can happen is if your learning rate is very high, for example, and you have a neural net with ReLU neurons, you train the neural net and you get some last loss.

And then actually what you do is you go through the entire training set and you forward your examples and you can find neurons that never activate. They are dead neurons in your network. And so those neurons will never turn on. And usually what happens is that during training, these ReLU neurons are changing, moving, etc.

And then because of a high gradient somewhere by chance, they get knocked off and then nothing ever activates them. And from then on, they are just dead. So that's kind of like a permanent brain damage that can happen to some of these neurons. These other nonlinearities like Leaky ReLU will not suffer from this issue as much because you can see that it doesn't have flat tails.

You'll almost always get gradients. And ELU is also fairly frequently used. It also might suffer from this issue because it has flat parts. So that's just something to be aware of and something to be concerned about. And in this case, we have way too many activations h that take on extreme values.

And because there's no column of white, I think we will be okay. And indeed, the network optimizes and gives us a pretty decent loss. But it's just not optimal. And this is not something you want, especially during initialization. And so basically what's happening is that this h pre-activation that's flowing to 10h, it's too extreme.

It's too large. It's creating a distribution that is too saturated in both sides of the 10h. And it's not something you want because it means that there's less training for these neurons because they update less frequently. So how do we fix this? Well, h pre-activation is mcat, which comes from c.

So these are uniform Gaussian. But then it's multiplied by w1 plus b1. And h pre-act is too far off from 0, and that's causing the issue. So we want this pre-activation to be closer to 0, very similar to what we had with logits. So here, we want actually something very, very similar.

Now it's okay to set the biases to a very small number. We can either multiply by 001 to get a little bit of entropy. I sometimes like to do that just so that there's a little bit of variation and diversity in the original initialization of these 10h neurons. And I find in practice that that can help optimization a little bit.

And then the weights, we can also just squash. So let's multiply everything by 0.1. Let's rerun the first batch. And now let's look at this. And well, first let's look at here. You see now, because we multiplied w by 0.1, we have a much better histogram. And that's because the pre-activations are now between -1.5 and 1.5.

And this, we expect much, much less white. Okay, there's no white. So basically, that's because there are no neurons that saturated above 0.99 in either direction. So it's actually a pretty decent place to be. Maybe we can go up a little bit. Sorry, am I changing w1 here? So maybe we can go to 0.2.

Okay, so maybe something like this is a nice distribution. So maybe this is what our initialization should be. So let me now erase these. And let me, starting with initialization, let me run the full optimization without the break. And let's see what we get. Okay, so the optimization finished.

And I rerun the loss. And this is the result that we get. And then just as a reminder, I put down all the losses that we saw previously in this lecture. So we see that we actually do get an improvement here. And just as a reminder, we started off with a validation loss of 2.17 when we started.

By fixing the softmax being confidently wrong, we came down to 2.13. And by fixing the 10H layer being way too saturated, we came down to 2.10. And the reason this is happening, of course, is because our initialization is better. And so we're spending more time doing productive training instead of not very productive training because our gradients are set to zero, and we have to learn very simple things like the overconfidence of the softmax in the beginning.

And we're spending cycles just like squashing down the weight matrix. So this is illustrating basically initialization and its impact on performance just by being aware of the internals of these neural nets and their activations and their gradients. Now we're working with a very small network. This is just one layer multilayer perceptron.

So because the network is so shallow, the optimization problem is actually quite easy and very forgiving. So even though our initialization was terrible, the network still learned eventually. It just got a bit worse result. This is not the case in general, though. Once we actually start working with much deeper networks that have, say, 50 layers, things can get much more complicated.

And these problems stack up. And so you can actually get into a place where the network is basically not training at all if your initialization is bad enough. And the deeper your network is and the more complex it is, the less forgiving it is to some of these errors.

And so something to definitely be aware of and something to scrutinize, something to plot and something to be careful with. And yeah. Okay, so that's great that that worked for us. But what we have here now is all these magic numbers like 0.2. Like where do I come up with this?

And how am I supposed to set these if I have a large neural network with lots and lots of layers? And so obviously no one does this by hand. There's actually some relatively principled ways of setting these scales that I would like to introduce to you now. So let me paste some code here that I prepared just to motivate the discussion of this.

So what I'm doing here is we have some random input here, X, that is drawn from a Gaussian. And there's 1,000 examples that are 10-dimensional. And then we have a weighting layer here that is also initialized using Gaussian, just like we did here. And these neurons in the hidden layer look at 10 inputs, and there are 200 neurons in this hidden layer.

And then we have here, just like here in this case, the multiplication, X multiplied by W to get the pre-activations of these neurons. And basically the analysis here looks at, okay, suppose these are uniform Gaussian and these weights are uniform Gaussian. If I do X times W, and we forget for now the bias and the nonlinearity, then what is the mean and the standard deviation of these Gaussians?

So in the beginning here, the input is just a normal Gaussian distribution. Mean is zero, and the standard deviation is one. And the standard deviation, again, is just the measure of a spread of this Gaussian. But then once we multiply here and we look at the histogram of Y, we see that the mean, of course, stays the same.

It's about zero, because this is a symmetric operation. But we see here that the standard deviation has expanded to three. So the input standard deviation was one, but now we've grown to three. And so what you're seeing in the histogram is that this Gaussian is expanding. And so we're expanding this Gaussian from the input.

And we don't want that. We want most of the neural net to have relatively similar activations. So unit Gaussian, roughly, throughout the neural net. And so the question is, how do we scale these Ws to preserve this distribution to remain a Gaussian? And so intuitively, if I multiply here these elements of W by a larger number, let's say by five, then this Gaussian grows and grows in standard deviation.

So now we're at 15. So basically, these numbers here in the output, Y, take on more and more extreme values. But if we scale it down, let's say 0.2, then conversely, this Gaussian is getting smaller and smaller. And it's shrinking. And you can see that the standard deviation is 0.6.

And so the question is, what do I multiply by here to exactly preserve the standard deviation to be one? And it turns out that the correct answer mathematically, when you work out through the variance of this multiplication here, is that you are supposed to divide by the square root of the fan in.

The fan in is basically the number of input elements here, 10. So we are supposed to divide by 10 square root. And this is one way to do the square root. You raise it to a power of 0.5. That's the same as doing a square root. So when you divide by the square root of 10, then we see that the output Gaussian, it has exactly standard deviation of 1.

Now unsurprisingly, a number of papers have looked into how to best initialize neural networks. And in the case of multilayer perceptrons, we can have fairly deep networks that have these nonlinearities in between. And we want to make sure that the activations are well-behaved and they don't expand to infinity or shrink all the way to 0.

And the question is, how do we initialize the weights so that these activations take on reasonable values throughout the network? Now one paper that has studied this in quite a bit of detail that is often referenced is this paper by Kaiming et al. called Delving Deep Interactive Fires. Now in this case, they actually studied convolutional neural networks.

And they studied especially the ReLU nonlinearity and the pReLU nonlinearity instead of a 10H nonlinearity. But the analysis is very similar. And basically what happens here is for them, the ReLU nonlinearity that they care about quite a bit here is a squashing function where all the negative numbers are simply clamped to 0.

So the positive numbers are a path through, but everything negative is just set to 0. And because you're basically throwing away half of the distribution, they find in their analysis of the forward activations in the neural net that you have to compensate for that with a gain. And so here, they find that basically when they initialize their weights, they have to do it with a zero-mean Gaussian whose standard deviation is square root of 2 over the Fannin.

What we have here is we are initializing the Gaussian with the square root of Fannin. This NL here is the Fannin. So what we have is square root of 1 over the Fannin because we have the division here. Now they have to add this factor of 2 because of the ReLU, which basically discards half of the distribution and clamps it at 0.

And so that's where you get an initial factor. Now in addition to that, this paper also studies not just the behavior of the activations in the forward pass of the neural net, but it also studies the backpropagation. And we have to make sure that the gradients also are well-behaved because ultimately, they end up updating our parameters.

And what they find here through a lot of the analysis that I invite you to read through, but it's not exactly approachable, what they find is basically if you properly initialize the forward pass, the backward pass is also approximately initialized up to a constant factor that has to do with the size of the number of hidden neurons in an early and late layer.

But basically they find empirically that this is not a choice that matters too much. Now this kyming initialization is also implemented in PyTorch. So if you go to torch.nn.init documentation, you'll find kyming normal. And in my opinion, this is probably the most common way of initializing neural networks now.

And it takes a few keyword arguments here. So number one, it wants to know the mode. Would you like to normalize the activations or would you like to normalize the gradients to be always Gaussian with zero mean and a unit or one standard deviation? And because they find in the paper that this doesn't matter too much, most of the people just leave it as the default, which is fan-in.

And then second, passing the nonlinearity that you are using. Because depending on the nonlinearity, we need to calculate a slightly different gain. And so if your nonlinearity is just linear, so there's no nonlinearity, then the gain here will be one. And we have the exact same kind of formula that we've got up here.

But if the nonlinearity is something else, we're going to get a slightly different gain. And so if we come up here to the top, we see that, for example, in the case of ReLU, this gain is a square root of two. And the reason it's a square root is because in this paper, you see how the two is inside of the square root, so the gain is a square root of two.

In the case of linear or identity, we just get a gain of one. In the case of 10H, which is what we're using here, the advised gain is a five over three. And intuitively, why do we need a gain on top of the initialization? It's because 10H, just like ReLU, is a contractive transformation.

So what that means is you're taking the output distribution from this matrix multiplication, and then you are squashing it in some way. Now ReLU squashes it by taking everything below zero and clamping it to zero. 10H also squashes it because it's a contractive operation. It will take the tails and it will squeeze them in.

And so in order to fight the squeezing in, we need to boost the weights a little bit so that we renormalize everything back to unit standard deviation. So that's why there's a little bit of a gain that comes out. Now I'm skipping through this section a little bit quickly, and I'm doing that actually intentionally.

And the reason for that is because about seven years ago when this paper was written, you had to actually be extremely careful with the activations and the gradients and their ranges and their histograms. And you had to be very careful with the precise setting of gains and the scrutinizing of the nonlinearities used and so on.

And everything was very finicky and very fragile and to be very properly arranged for the neural net to train, especially if your neural net was very deep. But there are a number of modern innovations that have made everything significantly more stable and more well-behaved. And it's become less important to initialize these networks exactly right.

And some of those modern innovations, for example, are residual connections, which we will cover in the future. The use of a number of normalization layers, like for example, batch normalization, layer normalization, group normalization, we're going to go into a lot of these as well. And number three, much better optimizers, not just stochastic gradient descent, the simple optimizer we're basically using here, but slightly more complex optimizers like RMSProp and especially Adam.

And so all of these modern innovations make it less important for you to precisely calibrate the initialization of the neural net. All that being said, in practice, what should we do? In practice, when I initialize these neural nets, I basically just normalize my weights by the square root of the fan-in.

So basically, roughly what we did here is what I do. Now, if we want to be exactly accurate here, and go back in it of timing normal, this is how we would implement it. We want to set the standard deviation to be gain over the square root of fan-in.

So to set the standard deviation of our weights, we will proceed as follows. Basically when we have a torsion type random, and let's say I just create a thousand numbers, we can look at the standard deviation of this, and of course that's one. That's the amount of spread. Let's make this a bit bigger so it's closer to one.

So that's the spread of the Gaussian of zero mean and unit standard deviation. Now basically when you take these and you multiply by say 0.2, that basically scales down the Gaussian and that makes its standard deviation 0.2. So basically the number that you multiply by here ends up being the standard deviation of this Gaussian.

So here this is a standard deviation 0.2 Gaussian here when we sample RW1. But we want to set the standard deviation to gain over square root of fan-in. So in other words, we want to multiply by gain, which for 10H is 5/3. 5/3 is the gain, and then times, or I guess sorry, divide square root of the fan-in.

In this example here the fan-in was 10, and I just noticed that actually here the fan-in for W1 is actually an embed times block size, which as you will recall is actually 30. And that's because each character is 10-dimensional, but then we have three of them and we concatenate them.

So actually the fan-in here was 30, and I should have used 30 here probably. But basically we want 30 square root. So this is the number, this is what our standard deviation we want to be, and this number turns out to be 0.3. Whereas here just by fiddling with it and looking at the distribution and making sure it looks okay, we came up with 0.2.

And so instead what we want to do here is we want to make the standard deviation be 5/3, which is our gain, divide this amount times 0.2 square root. And these brackets here are not that necessary, but I'll just put them here for clarity. This is basically what we want.

This is the kyming init in our case for 10H nonlinearity, and this is how we would initialize the neural net. And so we're multiplying by 0.3 instead of multiplying by 0.2. And so we can initialize this way, and then we can train the neural net and see what we get.

Okay, so I trained the neural net and we end up in roughly the same spot. So looking at the validation loss, we now get 2.10, and previously we also had 2.10. There's a little bit of a difference, but that's just the randomness of the process, I suspect. But the big deal, of course, is we get to the same spot, but we did not have to introduce any magic numbers that we got from just looking at histograms and guessing, checking.

We have something that is semi-principled and will scale us to much bigger networks and something that we can sort of use as a guide. So I mentioned that the precise setting of these initializations is not as important today due to some modern innovations. And I think now is a pretty good time to introduce one of those modern innovations, and that is batch normalization.

So batch normalization came out in 2015 from a team at Google, and it was an extremely impactful paper because it made it possible to train very deep neural nets quite reliably, and it basically just worked. So here's what batch normalization does and what's implemented. Basically we have these hidden states, H_preact, right?

And we were talking about how we don't want these preactivation states to be way too small because then the tanh is not doing anything, but we don't want them to be too large because then the tanh is saturated. In fact, we want them to be roughly Gaussian, so zero mean and a unit or one standard deviation, at least at initialization.

So the insight from the batch normalization paper is, okay, you have these hidden states and you'd like them to be roughly Gaussian, then why not take the hidden states and just normalize them to be Gaussian? And it sounds kind of crazy, but you can just do that because standardizing hidden states so that they're unit Gaussian is a perfectly differentiable operation, as we'll soon see.

And so that was kind of like the big insight in this paper, and when I first read it, my mind was blown because you can just normalize these hidden states, and if you'd like unit Gaussian states in your network, at least initialization, you can just normalize them to be unit Gaussian.

So let's see how that works. So we're going to scroll to our pre-activations here just before they enter into the tanh. Now the idea again is, remember, we're trying to make these roughly Gaussian, and that's because if these are way too small numbers, then the tanh here is kind of inactive.

But if these are very large numbers, then the tanh is way too saturated and gradient is no flow. So we'd like this to be roughly Gaussian. So the insight in batch normalization again is that we can just standardize these activations so they are exactly Gaussian. So here, H_preact has a shape of 32 by 200, 32 examples by 200 neurons in the hidden layer.

So basically what we can do is we can take H_preact and we can just calculate the mean, and the mean we want to calculate across the 0th dimension, and we want to also keep the missed true so that we can easily broadcast this. So the shape of this is 1 by 200.

In other words, we are doing the mean over all the elements in the batch. And similarly, we can calculate the standard deviation of these activations, and that will also be 1 by 200. Now in this paper, they have the sort of prescription here, and see here we are calculating the mean, which is just taking the average value of any neuron's activation, and then the standard deviation is basically kind of like the measure of the spread that we've been using, which is the distance of every one of these values away from the mean, and that squared and averaged.

That's the variance, and then if you want to take the standard deviation, you would square root the variance to get the standard deviation. So these are the two that we're calculating, and now we're going to normalize or standardize these x's by subtracting the mean and dividing by the standard deviation.

So basically, we're taking H_preact and we subtract the mean, and then we divide by the standard deviation. This is exactly what these two, std and mean, are calculating. This is the mean and this is the variance. You see how the sigma is the standard deviation usually, so this is sigma squared, which the variance is the square of the standard deviation.

So this is how you standardize these values, and what this will do is that every single neuron now, and its firing rate, will be exactly unit Gaussian on these 32 examples at least of this batch. That's why it's called batch normalization. We are normalizing these batches. And then we could, in principle, train this.

Notice that calculating the mean and your standard deviation, these are just mathematical formulas. They're perfectly differentiable. All of this is perfectly differentiable, and we can just train this. The problem is you actually won't achieve a very good result with this, and the reason for that is we want these to be roughly Gaussian, but only at initialization.

But we don't want these to be forced to be Gaussian always. We'd like to allow the neural net to move this around to potentially make it more diffuse, to make it more sharp, to make some 10H neurons maybe be more trigger happy or less trigger happy. So we'd like this distribution to move around, and we'd like the backpropagation to tell us how the distribution should move around.

And so in addition to this idea of standardizing the activations at any point in the network, we have to also introduce this additional component in the paper here described as scale and shift. And so basically what we're doing is we're taking these normalized inputs, and we are additionally scaling them by some gain and offsetting them by some bias to get our final output from this layer.

And so what that amounts to is the following. We are going to allow a batch normalization gain to be initialized at just a once, and the once will be in the shape of 1 by n hidden. And then we also will have a bn_bias, which will be torched at zeros, and it will also be of the shape 1 by n hidden.

And then here, the bn_gain will multiply this, and the bn_bias will offset it here. So because this is initialized to 1 and this to 0, at initialization, each neuron's firing values in this batch will be exactly unit Gaussian and will have nice numbers. No matter what the distribution of the H_preact is coming in, coming out, it will be unit Gaussian for each neuron, and that's roughly what we want, at least at initialization.

And then during optimization, we'll be able to backpropagate to bn_gain and bn_bias and change them so the network is given the full ability to do with this whatever it wants internally. Here we just have to make sure that we include these in the parameters of the neural net because they will be trained with backpropagation.

So let's initialize this, and then we should be able to train. And then we're going to also copy this line, which is the batch normalization layer here on a single line of code, and we're going to swing down here, and we're also going to do the exact same thing at test time here.

So similar to train time, we're going to normalize and then scale, and that's going to give us our train and validation loss. And we'll see in a second that we're actually going to change this a little bit, but for now I'm going to keep it this way. So I'm just going to wait for this to converge.

Okay, so I allowed the neural nets to converge here, and when we scroll down, we see that our validation loss here is 2.10, roughly, which I wrote down here. And we see that this is actually kind of comparable to some of the results that we've achieved previously. Now, I'm not actually expecting an improvement in this case, and that's because we are dealing with a very simple neural net that has just a single hidden layer.

So in fact, in this very simple case of just one hidden layer, we were able to actually calculate what the scale of W should be to make these preactivations already have a roughly Gaussian shape. So the batch normalization is not doing much here. But you might imagine that once you have a much deeper neural net that has lots of different types of operations, and there's also, for example, residual connections, which we'll cover, and so on, it will become basically very, very difficult to tune the scales of your weight matrices such that all the activations throughout the neural net are roughly Gaussian.

And so that's going to become very quickly intractable. But compared to that, it's going to be much, much easier to sprinkle batch normalization layers throughout the neural net. So in particular, it's common to look at every single linear layer like this one. This is a linear layer multiplying by a weight matrix and adding a bias.

Or for example, convolutions, which we'll cover later and also perform basically a multiplication with a weight matrix, but in a more spatially structured format. It's customary to take this linear layer or convolutional layer and append a batch normalization layer right after it to control the scale of these activations at every point in the neural net.

So we'd be adding these batch normal layers throughout the neural net. And then this controls the scale of these activations throughout the neural net. It doesn't require us to do perfect mathematics and care about the activation distributions for all these different types of neural network Lego building blocks that you might want to introduce into your neural net.

And it significantly stabilizes the training. And that's why these layers are quite popular. Now the stability offered by batch normalization actually comes at a terrible cost. And that cost is that if you think about what's happening here, something terribly strange and unnatural is happening. It used to be that we have a single example feeding into a neural net, and then we calculate its activations and its logits.

And this is a deterministic sort of process. So you arrive at some logits for this example. And then because of efficiency of training, we suddenly started to use batches of examples. But those batches of examples were processed independently, and it was just an efficiency thing. But now suddenly in batch normalization, because of the normalization through the batch, we are coupling these examples mathematically and in the forward pass and the backward pass of the neural net.

So now the hidden state activations, HPREACT, and your logits for any one input example are not just a function of that example and its input, but they're also a function of all the other examples that happen to come for a ride in that batch. And these examples are sampled randomly.

And so what's happening is, for example, when you look at HPREACT, that's going to feed into H, the hidden state activations, for example, for any one of these input examples, is going to actually change slightly depending on what other examples there are in the batch. And depending on what other examples happen to come for a ride, H is going to change suddenly and is going to jitter if you imagine sampling different examples, because the statistics of the mean and the standard deviation are going to be impacted.

And so you'll get a jitter for H, and you'll get a jitter for logits. And you'd think that this would be a bug or something undesirable, but in a very strange way, this actually turns out to be good in neural network training as a side effect. And the reason for that is that you can think of this as kind of like a regularizer, because what's happening is you have your input and you get your H, and then depending on the other examples, this is jittering a bit.

And so what that does is that it's effectively padding out any one of these input examples, and it's introducing a little bit of entropy. And because of the padding out, it's actually kind of like a form of data augmentation, which we'll cover in the future. And it's kind of like augmenting the input a little bit and jittering it, and that makes it harder for the neural nets to overfit to these concrete specific examples.

So by introducing all this noise, it actually like pads out the examples and it regularizes the neural net. And that's one of the reasons why deceivingly as a second order effect, this is actually a regularizer, and that has made it harder for us to remove the use of batch normalization.

Because basically no one likes this property that the examples in the batch are coupled mathematically and in the forward pass. And it leads to all kinds of like strange results. We'll go into some of that in a second as well. And it leads to a lot of bugs and so on.

And so no one likes this property. And so people have tried to deprecate the use of batch normalization and move to other normalization techniques that do not couple the examples of a batch. Examples are layer normalization, instance normalization, group normalization, and so on. And we'll come or we'll come or some of these later.

But basically long story short, batch normalization was the first kind of normalization layer to be introduced. It worked extremely well. It happens to have this regularizing effect. It stabilized training and people have been trying to remove it and move to some of the other normalization techniques. But it's been hard because it just works quite well.

And some of the reason that it works quite well is again because of this regularizing effect and because it is quite effective at controlling the activations and their distributions. So that's kind of like the brief story of batch normalization. And I'd like to show you one of the other weird sort of outcomes of this coupling.

So here's one of the strange outcomes that I only glossed over previously when I was evaluating the loss on the validation set. Basically once we've trained a neural net, we'd like to deploy it in some kind of a setting and we'd like to be able to feed in a single individual example and get a prediction out from our neural net.

But how do we do that when our neural net now in a forward pass estimates the statistics of the mean understated deviation of a batch? The neural net expects batches as an input now. So how do we feed in a single example and get sensible results out? And so the proposal in the batch normalization paper is the following.

What we would like to do here is we would like to basically have a step after training that calculates and sets the batch norm mean and standard deviation a single time over the training set. And so I wrote this code here in the interest of time and we're going to call what's called calibrate the batch norm statistics.

And basically what we do is Torch.nograd telling PyTorch that none of this we will call a dot backward on and it's going to be a bit more efficient. We're going to take the training set, get the preactivations for every single training example and then one single time estimate the mean and standard deviation over the entire training set.

And then we're going to get B and mean and B and standard deviation. And now these are fixed numbers estimating over the entire training set. And here instead of estimating it dynamically, we are going to instead here use B and mean and here we're just going to use B and standard deviation.

And so at test time, we are going to fix these, clamp them and use them during inference. And now you see that we get basically identical result. But the benefit that we've gained is that we can now also forward a single example because the mean and standard deviation are now fixed sort of tensors.

That said, nobody actually wants to estimate this mean and standard deviation as a second stage after neural network training because everyone is lazy. And so this batch normalization paper actually introduced one more idea, which is that we can estimate the mean and standard deviation in a running manner during training of the neural net.

And then we can simply just have a single stage of training. And on the side of that training, we are estimating the running mean and standard deviation. So let's see what that would look like. Let me basically take the mean here that we are estimating on the batch and let me call this B and mean on the i-th iteration.

And then here, this is B and STD. B and STD at i. And the mean comes here and the STD comes here. So so far, I've done nothing. I've just moved around and I created these extra variables for the mean and standard deviation and I've put them here. So so far, nothing has changed.

But what we're going to do now is we're going to keep a running mean of both of these values during training. So let me swing up here and let me create a B and mean underscore running. And I'm going to initialize it at zeros and then B and STD running, which I'll initialize at ones.

Because in the beginning, because of the way we initialized W1 and B1, HPREACT will be roughly unit Gaussian, so the mean will be roughly zero and the standard deviation roughly one. So I'm going to initialize these that way. But then here, I'm going to update these. And in PyTorch, these mean and standard deviation that are running, they're not actually part of the gradient based optimization.

We're never going to derive gradients with respect to them. They're updated on the side of training. And so what we're going to do here is we're going to say with torch.nograd, telling PyTorch that the update here is not supposed to be building out a graph because there will be no dot backward.

But this running mean is basically going to be 0.999 times the current value plus 0.001 times this value, this new mean. And in the same way, BNSTDRunning will be mostly what it used to be, but it will receive a small update in the direction of what the current standard deviation is.

And as you're seeing here, this update is outside and on the side of the gradient based optimization. And it's simply being updated not using gradient descent, it's just being updated using a janky, like smooth, sort of running mean manner. And so while the network is training and these preactivations are sort of changing and shifting around during backpropagation, we are keeping track of the typical mean and standard deviation and we're estimating them once.

And when I run this, now I'm keeping track of this in a running manner. And what we're hoping for, of course, is that the BNMean_running and BNMean_backpropagation or STD are going to be very similar to the ones that we calculated here before. And that way, we don't need a second stage because we've sort of combined the two stages and we've put them on the side of each other, if you want to look at it that way.

And this is how this is also implemented in the batch normalization layer in PyTorch. So during training, the exact same thing will happen. And then later when you're using inference, it will use the estimated running mean of both the mean and standard deviation of those hidden states. So let's wait for the optimization to converge and hopefully the running mean and standard deviation are roughly equal to these two.

And then we can simply use it here and we don't need this stage of explicit calibration at the end. Okay, so the optimization finished. I'll rerun the explicit estimation. And then the BNMean from the explicit estimation is here. And BNMean from the running estimation during the optimization, you can see is very, very similar.

It's not identical, but it's pretty close. And in the same way, BNSTD is this and BNSTDRunning is this. As you can see that once again, they are fairly similar values, not identical, but pretty close. And so then here, instead of BNMean, we can use the BNMean running. Instead of BNSTD, we can use BNSTDRunning.

And hopefully the validation loss will not be impacted too much. Okay, so basically identical. And this way, we've eliminated the need for this explicit stage of calibration because we are doing it in line over here. Okay, so we're almost done with batch normalization. There are only two more notes that I'd like to make.

Number one, I've skipped a discussion over what is this plus epsilon doing here. This epsilon is usually like some small fixed number, for example, 1E negative 5 by default. And what it's doing is that it's basically preventing a division by zero in the case that the variance over your batch is exactly zero.

In that case, here we'd normally have a division by zero, but because of the plus epsilon, this is going to become a small number in the denominator instead, and things will be more well-behaved. So feel free to also add a plus epsilon here of a very small number. It doesn't actually substantially change the result.

I'm going to skip it in our case just because this is unlikely to happen in our very simple example here. And the second thing I want you to notice is that we're being wasteful here, and it's very subtle. But right here where we are adding the bias into HPREACT, these biases now are actually useless because we're adding them to the HPREACT.

But then we are calculating the mean for every one of these neurons and subtracting it. So whatever bias you add here is going to get subtracted right here. And so these biases are not doing anything. In fact, they're being subtracted out, and they don't impact the rest of the calculation.

So if you look at B1.grad, it's actually going to be zero because it's being subtracted out and doesn't actually have any effect. And so whenever you're using batch normalization layers, then if you have any weight layers before, like a linear or a conv or something like that, you're better off coming here and just not using bias.

So you don't want to use bias, and then here you don't want to add it because that's spurious. Instead we have this batch normalization bias here, and that batch normalization bias is now in charge of the biasing of this distribution instead of this B1 that we had here originally.

And so basically the batch normalization layer has its own bias, and there's no need to have a bias in the layer before it because that bias is going to be subtracted out anyway. So that's the other small detail to be careful with. Sometimes it's not going to do anything catastrophic.

This B1 will just be useless. It will never get any gradient. It will not learn. It will stay constant, and it's just wasteful, but it doesn't actually really impact anything otherwise. Okay, so I rearranged the code a little bit with comments, and I just wanted to give a very quick summary of the batch normalization layer.

We are using batch normalization to control the statistics of activations in the neural net. It is common to sprinkle batch normalization layer across the neural net, and usually we will place it after layers that have multiplications, like for example a linear layer or a convolutional layer, which we may cover in the future.

Now the batch normalization internally has parameters for the gain and the bias, and these are trained using backpropagation. It also has two buffers. The buffers are the mean and the standard deviation, the running mean and the running mean of the standard deviation. And these are not trained using backpropagation.

These are trained using this janky update of kind of like a running mean update. So these are sort of the parameters and the buffers of batch normalization layer. And then really what it's doing is it's calculating the mean and the standard deviation of the activations that are feeding into the batch normalization layer over that batch.

Then it's centering that batch to be unit Gaussian, and then it's offsetting and scaling it by the learned bias and gain. And then on top of that, it's keeping track of the mean and standard deviation of the inputs, and it's maintaining this running mean and standard deviation. And this will later be used at inference so that we don't have to re-estimate the mean and standard deviation all the time.

And in addition, that allows us to basically forward individual examples at test time. So that's the batch normalization layer. It's a fairly complicated layer, but this is what it's doing internally. Now I wanted to show you a little bit of a real example. So you can search ResNet, which is a residual neural network, and these are contacts of neural networks used for image classification.

And of course, we haven't covered ResNets in detail, so I'm not going to explain all the pieces of it. But for now, just note that the image feeds into a ResNet on the top here, and there's many, many layers with repeating structure all the way to predictions of what's inside that image.

This repeating structure is made up of these blocks, and these blocks are just sequentially stacked up in this deep neural network. Now the code for this, the block basically that's used and repeated sequentially in series, is called this bottleneck block. And there's a lot here. This is all PyTorch, and of course we haven't covered all of it, but I want to point out some small pieces of it.

Here in the init is where we initialize the neural net. So this code of block here is basically the kind of stuff we're doing here. We're initializing all the layers. And in the forward, we are specifying how the neural net acts once you actually have the input. So this code here is along the lines of what we're doing here.

And now these blocks are replicated and stacked up serially, and that's what a residual network would be. And so notice what's happening here. Conv1, these are convolution layers. And these convolution layers basically, they're the same thing as a linear layer, except convolution layers don't apply, convolution layers are used for images.

And so they have spatial structure. And basically this linear multiplication and bias offset are done on patches instead of a map, instead of the full input. So because these images have structure, spatial structure, convolutions just basically do WX plus B, but they do it on overlapping patches of the input.

But otherwise it's WX plus B. Then we have the normal layer, which by default here is initialized to be a batch norm in 2D, so two-dimensional batch normalization layer. And then we have a nonlinearity like ReLU. So instead of, here they use ReLU, we are using tanh in this case.

But both are just nonlinearities and you can just use them relatively interchangeably. For very deep networks, ReLUs typically empirically work a bit better. So see the motif that's being repeated here. We have convolution, batch normalization, ReLU, convolution, batch normalization, ReLU, etc. And then here, this is a residual connection that we haven't covered yet.

But basically that's the exact same pattern we have here. We have a weight layer, like a convolution or like a linear layer, batch normalization, and then tanh, which is nonlinearity. But basically a weight layer, a normalization layer, and nonlinearity. And that's the motif that you would be stacking up when you create these deep neural networks, exactly as is done here.

And one more thing I'd like you to notice is that here when they are initializing the conv layers, like conv1x1, the depth for that is right here. And so it's initializing an nn.conv2d, which is a convolution layer in PyTorch. And there's a bunch of keyword arguments here that I'm not going to explain yet, but you see how there's bias equals false?

The bias equals false is exactly for the same reason as bias is not used in our case. You see how I erased the use of bias? And the use of bias is spurious because after this weight layer, there's a batch normalization. And the batch normalization subtracts that bias and then has its own bias.

So there's no need to introduce these spurious parameters. It wouldn't hurt performance, it's just useless. And so because they have this motif of conv, batch, and relu, they don't need a bias here because there's a bias inside here. So by the way, this example here is very easy to find.

Just do ResNetPyTorch, and it's this example here. So this is kind of like the stock implementation of a residual neural network in PyTorch. And you can find that here. But of course, I haven't covered many of these parts yet. And I would also like to briefly descend into the definitions of these PyTorch layers and the parameters that they take.

Now instead of a convolutional layer, we're going to look at a linear layer because that's the one that we're using here. This is a linear layer, and I haven't covered convolutions yet. But as I mentioned, convolutions are basically linear layers except on patches. So a linear layer performs a WX+B, except here they're calling the W a transpose.

So it calculates WX+B very much like we did here. To initialize this layer, you need to know the fan in, the fan out, and that's so that they can initialize this W. This is the fan in and the fan out. So they know how big the weight matrix should be.

You need to also pass in whether or not you want a bias. And if you set it to false, then no bias will be inside this layer. And you may want to do that exactly like in our case, if your layer is followed by a normalization layer such as batch norm.

So this allows you to basically disable bias. In terms of the initialization, if we swing down here, this is reporting the variables used inside this linear layer. And our linear layer here has two parameters, the weight and the bias. In the same way, they have a weight and a bias.

And they're talking about how they initialize it by default. So by default, PyTorch will initialize your weights by taking the fan in and then doing 1/fanin square root. And then instead of a normal distribution, they are using a uniform distribution. So it's very much the same thing, but they are using a 1 instead of 5/3, so there's no gain being calculated here.

The gain is just 1. But otherwise, it's exactly 1/the square root of fanin, exactly as we have here. So 1/the square root of k is the scale of the weights. But when they are drawing the numbers, they're not using a Gaussian by default. They're using a uniform distribution by default.

And so they draw uniformly from negative square root of k to square root of k. But it's the exact same thing and the same motivation with respect to what we've seen in this lecture. And the reason they're doing this is if you have a roughly Gaussian input, this will ensure that out of this layer, you will have a roughly Gaussian output.

And you basically achieve that by scaling the weights by 1/the square root of fanin. So that's what this is doing. And then the second thing is the batch normalization layer. So let's look at what that looks like in PyTorch. So here we have a one-dimensional batch normalization layer, exactly as we are using here.

And there are a number of keyword arguments going into it as well. So we need to know the number of features. For us, that is 200. And that is needed so that we can initialize these parameters here, the gain, the bias, and the buffers for the running mean and standard deviation.

Then they need to know the value of epsilon here. And by default, this is 1.5. You don't typically change this too much. Then they need to know the momentum. And the momentum here, as they explain, is basically used for these running mean and running standard deviation. So by default, the momentum here is 0.1.

The momentum we are using here in this example is 0.001. And basically, you may want to change this sometimes. And roughly speaking, if you have a very large batch size, then typically what you'll see is that when you estimate the mean and standard deviation for every single batch size, if it's large enough, you're going to get roughly the same result.

And so therefore, you can use slightly higher momentum, like 0.1. But for a batch size as small as 32, the mean and standard deviation here might take on slightly different numbers, because there's only 32 examples we are using to estimate the mean and standard deviation. So the value is changing around a lot.

And if your momentum is 0.1, that might not be good enough for this value to settle and converge to the actual mean and standard deviation over the entire training set. And so basically, if your batch size is very small, momentum of 0.1 is potentially dangerous, and it might make it so that the running mean and standard deviation is thrashing too much during training, and it's not actually converging properly.

Affine equals true determines whether this batch normalization layer has these learnable affine parameters, the gain and the bias. And this is almost always kept to true. I'm not actually sure why you would want to change this to false. Then track running stats is determining whether or not batch normalization layer of PyTorch will be doing this.

And one reason you may want to skip the running stats is because you may want to, for example, estimate them at the end as a stage two, like this. And in that case, you don't want the batch normalization layer to be doing all this extra compute that you're not going to use.

And finally, we need to know which device we're going to run this batch normalization on, a CPU or a GPU, and what the data type should be, half precision, single precision, double precision, and so on. So that's the batch normalization layer. Otherwise, they link to the paper. It's the same formula we've implemented, and everything is the same, exactly as we've done here.

Okay, so that's everything that I wanted to cover for this lecture. Really what I wanted to talk about is the importance of understanding the activations and the gradients and their statistics in neural networks. And this becomes increasingly important, especially as you make your neural networks bigger, larger, and deeper.

We looked at the distributions basically at the output layer, and we saw that if you have two confident mispredictions because the activations are too messed up at the last layer, you can end up with these hockey stick losses. And if you fix this, you get a better loss at the end of training because your training is not doing wasteful work.

Then we also saw that we need to control the activations. We don't want them to squash to zero or explode to infinity, because that you can run into a lot of trouble with all of these nonlinearities in these neural nets. And basically you want everything to be fairly homogeneous throughout the neural net.

You want roughly Gaussian activations throughout the neural net. Then we talked about, okay, if we want roughly Gaussian activations, how do we scale these weight matrices and biases during initialization of the neural net so that we don't get, you know, so everything is as controlled as possible? So that gave us a large boost and improvement.

And then I talked about how that strategy is not actually possible for much, much deeper neural nets, because when you have much deeper neural nets with lots of different types of layers, it becomes really, really hard to precisely set the weights and the biases in such a way that the activations are roughly uniform throughout the neural net.

So then I introduced the notion of a normalization layer. Now there are many normalization layers that people use in practice. Batch normalization, layer normalization, instance normalization, group normalization. We haven't covered most of them, but I've introduced the first one and also the one that I believe came out first, and that's called batch normalization.

And we saw how batch normalization works. This is a layer that you can sprinkle throughout your deep neural net. And the basic idea is if you want roughly Gaussian activations, well then take your activations and take the mean and the standard deviation and center your data. And you can do that because the centering operation is differentiable.

But on top of that, we actually had to add a lot of bells and whistles, and that gave you a sense of the complexities of the batch normalization layer, because now we're centering the data, that's great, but suddenly we need the gain and the bias, and now those are trainable.

And then because we are coupling all the training examples, now suddenly the question is how do you do the inference? Well, to do the inference, we need to now estimate these mean and standard deviation once over the entire training set, and then use those at inference. But then no one likes to do stage two, so instead we fold everything into the batch normalization layer during training and try to estimate these in a running manner so that everything is a bit simpler.

And that gives us the batch normalization layer. And as I mentioned, no one likes this layer. It causes a huge amount of bugs. And intuitively it's because it is coupling examples in the forward pass of the neural net. And I've shot myself in the foot with this layer over and over again in my life, and I don't want you to suffer the same.

So basically try to avoid it as much as possible. Some of the other alternatives to these layers are, for example, group normalization or layer normalization, and those have become more common in more recent deep learning, but we haven't covered those yet. But definitely batch normalization was very influential at the time when it came out in roughly 2015, because it was kind of the first time that you could train reliably much deeper neural nets.

And fundamentally the reason for that is because this layer was very effective at controlling the statistics of the activations in the neural net. So that's the story so far. And that's all I wanted to cover. And in the future lectures, hopefully we can start going into recurrent neural nets.

And recurrent neural nets, as we'll see, are just very, very deep networks, because you unroll the loop when you actually optimize these neural nets. And that's where a lot of this analysis around the activation statistics and all these normalization layers will become very, very important for good performance. So we'll see that next time.

Bye. Okay, so I lied. I would like us to do one more summary here as a bonus. And I think it's useful as to have one more summary of everything I've presented in this lecture. But also I would like us to start PyTorchifying our code a little bit, so it looks much more like what you would encounter in PyTorch.

So you'll see that I will structure our code into these modules, like a linear module and a batch form module. And I'm putting the code inside these modules so that we can construct neural networks very much like we would construct them in PyTorch. And I will go through this in detail.

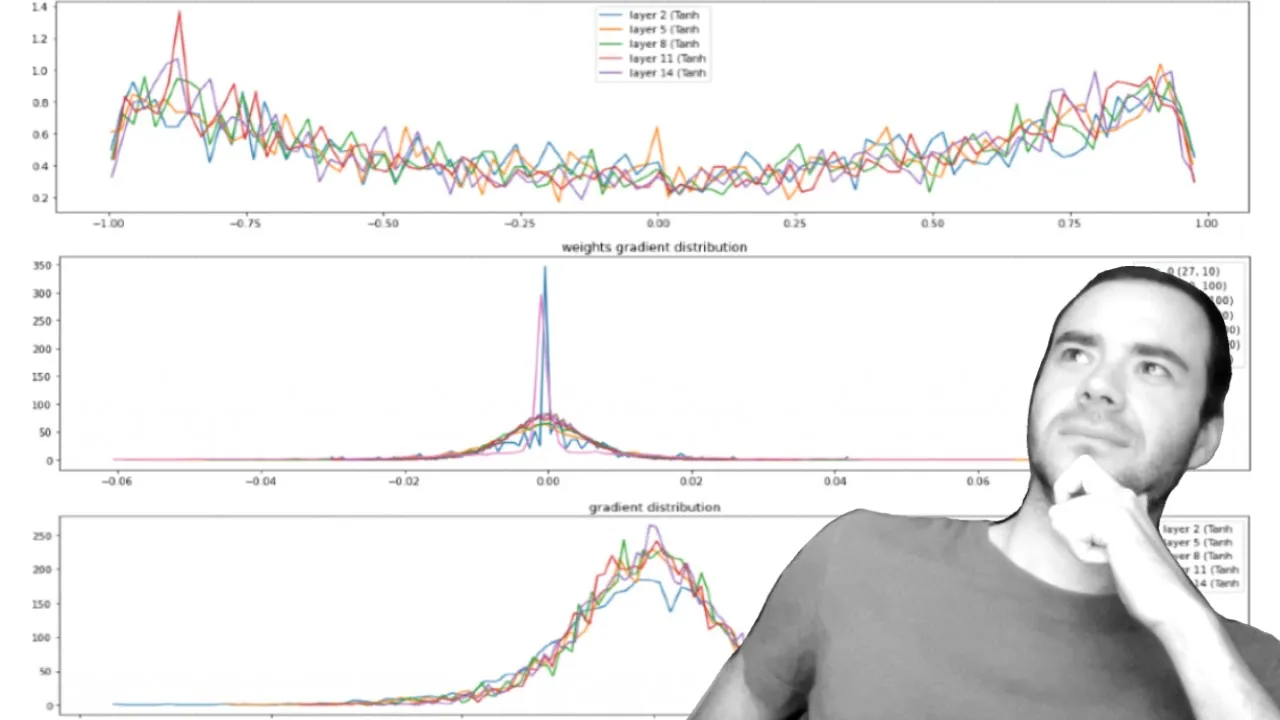
So we'll create our neural net. Then we will do the optimization loop, as we did before. And then the one more thing that I want to do here is I want to look at the activation statistics, both in the forward pass and in the backward pass. And then here we have the evaluation and sampling just like before.

So let me rewind all the way up here and go a little bit slower. So here I am creating a linear layer. You'll notice that torch.nn has lots of different types of layers. And one of those layers is the linear layer. torch.nn.linear takes a number of input features, output features, whether or not we should have a bias, and then the device that we want to place this layer on, and the data type.

So I will omit these two, but otherwise we have the exact same thing. We have the fan_in, which is the number of inputs, fan_out, the number of outputs, and whether or not we want to use a bias. And internally inside this layer, there's a weight and a bias, if you'd like it.

It is typical to initialize the weight using, say, random numbers drawn from a Gaussian. And then here's the kyming initialization that we discussed already in this lecture. And that's a good default, and also the default that I believe PyTorch uses. And by default, the bias is usually initialized to zeros.

Now when you call this module, this will basically calculate w times x plus b, if you have nb. And then when you also call .parameters on this module, it will return the tensors that are the parameters of this layer. Now next, we have the batch normalization layer. So I've written that here.

And this is very similar to PyTorch's nn.batchnorm1d layer, as shown here. So I'm kind of taking these three parameters here, the dimensionality, the epsilon that we'll use in the division, and the momentum that we will use in keeping track of these running stats, the running mean and the running variance.

Now PyTorch actually takes quite a few more things, but I'm assuming some of their settings. So for us, alphan will be true. That means that we will be using a gamma and beta after the normalization. The track running stats will be true, so we will be keeping track of the running mean and the running variance in the batch norm.

Our device by default is the CPU, and the data type by default is float, float32. So those are the defaults. Otherwise, we are taking all the same parameters in this batch norm layer. So first, I'm just saving them. Now here's something new. There's a .training, which by default is true.

And PyTorch nn modules also have this attribute, .training. And that's because many modules, and batch norm is included in that, have a different behavior whether you are training your neural net or whether you are running it in an evaluation mode and calculating your evaluation loss or using it for inference on some test examples.

And batch norm is an example of this, because when we are training, we are going to be using the mean and the variance estimated from the current batch. But during inference, we are using the running mean and running variance. And so also, if we are training, we are updating mean and variance.

But if we are testing, then these are not being updated. They're kept fixed. And so this flag is necessary and by default true, just like in PyTorch. Now the parameters of batch norm 1D are the gamma and the beta here. And then the running mean and the running variance are called buffers in PyTorch nomenclature.

And these buffers are trained using exponential moving average here explicitly. And they are not part of the backpropagation and stochastic gradient descent. So they are not parameters of this layer. And that's why when we have parameters here, we only return gamma and beta. We do not return the mean and the variance.

This is trained internally here, every forward pass, using exponential moving average. So that's the initialization. Now in a forward pass, if we are training, then we use the mean and the variance estimated by the batch. Let me pull up the paper here. We calculate the mean and the variance.

Now up above, I was estimating the standard deviation and keeping track of the standard deviation here in the running standard deviation instead of running variance. But let's follow the paper exactly. Here they calculate the variance, which is the standard deviation squared. And that's what's kept track of in the running variance instead of the running standard deviation.

But those two would be very, very similar, I believe. If we are not training, then we use the running mean and variance. We normalize. And then here, I'm calculating the output of this layer. And I'm also assigning it to an attribute called dot out. Now dot out is something that I'm using in our modules here.

This is not what you would find in PyTorch. We are slightly deviating from it. I'm creating a dot out because I would like to very easily maintain all those variables so that we can create statistics of them and plot them. But PyTorch and modules will not have a dot out attribute.

And finally here, we are updating the buffers using, again, as I mentioned, exponential moving average given the provided momentum. And importantly, you'll notice that I'm using the torch.nograd context manager. And I'm doing this because if we don't use this, then PyTorch will start building out an entire computational graph out of these tensors because it is expecting that we will eventually call dot backward.

But we are never going to be calling dot backward on anything that includes running mean and running variance. So that's why we need to use this context manager so that we are not sort of maintaining and using all this additional memory. So this will make it more efficient. And it's just telling PyTorch that there will be no backward.

We just have a bunch of tensors. We want to update them. That's it. And then we return. OK, now scrolling down, we have the 10H layer. This is very, very similar to torch.10H. And it doesn't do too much. It just calculates 10H, as you might expect. So that's torch.10H.

And there's no parameters in this layer. But because these are layers, it now becomes very easy to sort of stack them up into basically just a list. And we can do all the initializations that we're used to. So we have the initial sort of embedding matrix. We have our layers.

And we can call them sequentially. And then again, with torch.nograd, there's some initializations here. So we want to make the outputs of max a bit less confident, like we saw. And in addition to that, because we are using a six-layer multilayer perceptron here-- so you see how I'm stacking linear, 10H, linear, 10H, et cetera-- I'm going to be using the gain here.

And I'm going to play with this in a second. So you'll see how when we change this, what happens to the statistics. Finally, the parameters are basically the embedding matrix and all the parameters in all the layers. And notice here, I'm using a double list comprehension, if you want to call it that.

But for every layer in layers and for every parameter in each of those layers, we are just stacking up all those p's, all those parameters. Now in total, we have 46,000 parameters. And I'm telling PyTorch that all of them require gradient. Then here, we have everything here we are actually mostly used to.

We are sampling batch. We are doing forward pass. The forward pass now is just a linear application of all the layers in order, followed by the cross entropy. And then in the backward pass, you'll notice that for every single layer, I now iterate over all the outputs. And I'm telling PyTorch to retain the gradient of them.

And then here, we are already used to all the gradients set to none, do the backward to fill in the gradients, do an update using stochastic gradient send, and then track some statistics. And then I am going to break after a single iteration. Now here in this cell, in this diagram, I am visualizing the histograms of the forward pass activations.

And I am specifically doing it at the 10-H layers. So iterating over all the layers, except for the very last one, which is basically just the softmax layer. If it is a 10-H layer, and I'm using a 10-H layer just because they have a finite output, negative one to one.

And so it's very easy to visualize here. So you see negative one to one. And it's a finite range and easy to work with. I take the out tensor from that layer into T. And then I'm calculating the mean, the standard deviation, and the percent saturation of T. And the way I define the percent saturation is that T dot absolute value is greater than 0.97.

So that means we are here at the tails of the 10-H. And remember that when we are in the tails of the 10-H, that will actually stop gradients. So we don't want this to be too high. Now here, I'm calling torch dot histogram. And then I am plotting this histogram.

So basically what this is doing is that every different type of layer-- and they all have a different color-- we are looking at how many values in these tensors take on any of the values below on this axis here. So the first layer is fairly saturated here at 20%.

So you can see that it's got tails here. But then everything sort of stabilizes. And if we had more layers here, it would actually just stabilize at around the standard deviation of about 0.65. And the saturation would be roughly 5%. And the reason that this stabilizes and gives us a nice distribution here is because gain is set to 5/3.

Now here, this gain, you see that by default, we initialize with 1 over square root of fan in. But then here during initialization, I come in and I iterate over all the layers. And if it's a linear layer, I boost that by the gain. Now we saw that 1-- so basically, if we just do not use a gain, then what happens?

If I redraw this, you will see that the standard deviation is shrinking and the saturation is coming to 0. And basically what's happening is the first layer is pretty decent. But then further layers are just kind of like shrinking down to 0. And it's happening slowly, but it's shrinking to 0.

And the reason for that is when you just have a sandwich of linear layers alone, then initializing our weights in this manner we saw previously would have conserved the standard deviation of 1. But because we have this interspersed tanh layers in there, these tanh layers are squashing functions. And so they take your distribution and they slightly squash it.

And so some gain is necessary to keep expanding it to fight the squashing. So it just turns out that 5/3 is a good value. So if we have something too small like 1, we saw that things will come towards 0. But if it's something too high, let's do 2.

Then here we see that-- well, let me do something a bit more extreme so it's a bit more visible. Let's try 3. OK, so we see here that the saturations are starting to be way too large. So 3 would create way too saturated activations. So 5/3 is a good setting for a sandwich of linear layers with tanh activations.

And it roughly stabilizes the standard deviation at a reasonable point. Now, honestly, I have no idea where 5/3 came from in PyTorch when we were looking at the counting initialization. I see empirically that it stabilizes this sandwich of linear and tanh and that the saturation is in a good range.

But I don't actually know if this came out of some math formula. I tried searching briefly for where this comes from, but I wasn't able to find anything. But certainly we see that empirically these are very nice ranges. Our saturation is roughly 5%, which is a pretty good number.

And this is a good setting of the gain in this context. Similarly, we can do the exact same thing with the gradients. So here is a very same loop if it's a tanh. But instead of taking the layer dot out, I'm taking the grad. And then I'm also showing the mean and the standard deviation.

And I'm plotting the histogram of these values. And so you'll see that the gradient distribution is fairly reasonable. And in particular, what we're looking for is that all the different layers in this sandwich has roughly the same gradient. Things are not shrinking or exploding. So we can, for example, come here and we can take a look at what happens if this gain was way too small.

So this was 0.5. Then you see the first of all, the activations are shrinking to zero, but also the gradients are doing something weird. The gradient started off here, and then now they're expanding out. And similarly, if we, for example, have a too high of a gain, so like 3, then we see that also the gradients have-- there's some asymmetry going on where as you go into deeper and deeper layers, the activations are also changing.

And so that's not what we want. And in this case, we saw that without the use of BatchNorm, as we are going through right now, we have to very carefully set those gains to get nice activations in both the forward pass and the backward pass. Now before we move on to BatchNormalization, I would also like to take a look at what happens when we have no 10H units here.

So erasing all the 10H nonlinearities, but keeping the gain at 5/3, we now have just a giant linear sandwich. So let's see what happens to the activations. As we saw before, the correct gain here is 1. That is the standard deviation preserving gain. So 1.667 is too high. And so what's going to happen now is the following.

I have to change this to be linear, because there's no more 10H layers. And let me change this to linear as well. So what we're seeing is the activations started out on the blue and have, by layer four, become very diffuse. So what's happening to the activations is this.

And with the gradients on the top layer, the activation, the gradient statistics are the purple, and then they diminish as you go down deeper in the layers. And so basically you have an asymmetry in the neural net. And you might imagine that if you have very deep neural networks, say like 50 layers or something like that, this is not a good place to be.

So that's why before BatchNormalization, this was incredibly tricky to set. In particular, if this is too large of a gain, this happens, and if it's too little of a gain, then this happens. So the opposite of that basically happens. Here we have a shrinking and a diffusion, depending on which direction you look at it from.

And so certainly this is not what you want. And in this case, the correct setting of the gain is exactly 1, just like we're doing at initialization. And then we see that the statistics for the forward and the backward paths are well-behaved. And so the reason I want to show you this is that basically getting neural nets to train before these normalization layers and before the use of advanced optimizers like Adam, which we still have to cover, and residual connections and so on, training neural nets basically looked like this.

It's like a total balancing act. You have to make sure that everything is precisely orchestrated, and you have to care about the activations and the gradients and their statistics, and then maybe you can train something. But it was basically impossible to train very deep networks, and this is fundamentally the reason for that.

You'd have to be very, very careful with your initialization. The other point here is, you might be asking yourself, by the way, I'm not sure if I covered this, why do we need these 10H layers at all? Why do we include them and then have to worry about the gain?

And the reason for that, of course, is that if you just have a stack of linear layers, then certainly we're getting very easily nice activations and so on, but this is just a massive linear sandwich, and it turns out that it collapses to a single linear layer in terms of its representation power.

So if you were to plot the output as a function of the input, you're just getting a linear function. No matter how many linear layers you stack up, you still just end up with a linear transformation. All the WX plus Bs just collapse into a large WX plus B with slightly different Ws and slightly different B.

But interestingly, even though the forward pass collapses to just a linear layer, because of back propagation and the dynamics of the backward pass, the optimization actually is not identical. You actually end up with all kinds of interesting dynamics in the backward pass because of the way the chain rule is calculating it.

And so optimizing a linear layer by itself and optimizing a sandwich of 10 linear layers, in both cases those are just a linear transformation in the forward pass, but the training dynamics would be different. And there's entire papers that analyze, in fact, infinitely layered linear layers and so on.

And so there's a lot of things that you can play with there. But basically the 10-H nonlinearities allow us to turn this sandwich from just a linear chain into a neural network that can, in principle, approximate any arbitrary function. Okay, so now I've reset the code to use the linear 10-H sandwich like before, and I've reset everything so the gain is 5 over 3.

We can run a single step of optimization and we can look at the activation statistics of the forward pass and the backward pass. But I've added one more plot here that I think is really important to look at when you're training your neural nets and to consider. And ultimately what we're doing is we're updating the parameters of the neural net.

So we care about the parameters and their values and their gradients. So here what I'm doing is I'm actually iterating over all the parameters available and then I'm only restricting it to the two-dimensional parameters, which are basically the weights of these linear layers. And I'm skipping the biases and I'm skipping the gammas and the betas and the bastrom just for simplicity.

But you can also take a look at those as well. But what's happening with the weights is instructive by itself. So here we have all the different weights, their shapes. So this is the embedding layer, the first linear layer, all the way to the very last linear layer. And then we have the mean, the standard deviation of all these parameters.

The histogram, and you can see that it actually doesn't look that amazing, so there's some trouble in paradise. Even though these gradients looked okay, there's something weird going on here. I'll get to that in a second. And the last thing here is the gradient to data ratio. So sometimes I like to visualize this as well because what this gives you a sense of is what is the scale of the gradient compared to the scale of the actual values.

And this is important because we're going to end up taking a step update that is the learning rate times the gradient onto the data. And so if the gradient has too large of a magnitude, if the numbers in there are too large compared to the numbers in data, then you'd be in trouble.

But in this case, the gradient to data is our low numbers. So the values inside grad are 1000 times smaller than the values inside data in these weights, most of them. Now notably, that is not true about the last layer. And so the last layer actually here, the output layer, is a bit of a troublemaker in the way that this is currently arranged.

Because you can see that the last layer here in pink takes on values that are much larger than some of the values inside the neural net. So the standard deviations are roughly 1 and -3 throughout, except for the last layer, which actually has roughly 1 and -2 standard deviation of gradients.

And so the gradients on the last layer are currently about 100 times greater, sorry, 10 times greater than all the other weights inside the neural net. And so that's problematic because in the simple stochastic gradient descent setup, you would be training this last layer about 10 times faster than you would be training the other layers at initialization.

Now this actually kind of fixes itself a little bit if you train for a bit longer. So for example, if I greater than 1000, only then do a break. Let me reinitialize, and then let me do it 1000 steps. And after 1000 steps, we can look at the forward pass.

So you see how the neurons are saturating a bit. And we can also look at the backward pass. But otherwise they look good. They're about equal, and there's no shrinking to zero or exploding to infinities. And you can see that here in the weights, things are also stabilizing a little bit.

So the tails of the last pink layer are actually coming in during the optimization. But certainly this is a little bit troubling, especially if you are using a very simple update rule like stochastic gradient descent instead of a modern optimizer like Atom. Now I'd like to show you one more plot that I usually look at when I train neural networks.

And basically the gradient to data ratio is not actually that informative. Because what matters at the end is not the gradient to data ratio, but the update to the data ratio. Because that is the amount by which we will actually change the data in these tensors. So coming up here, what I'd like to do is I'd like to introduce a new update to data ratio.

It's going to be a list, and we're going to build it out every single iteration. And here I'd like to keep track of basically the ratio every single iteration. So without any gradients, I'm comparing the update, which is learning rate times the gradient. That is the update that we're going to apply to every parameter.

So see I'm iterating over all the parameters. And then I'm taking the basically standard deviation of the update we're going to apply and divide it by the actual content, the data of that parameter and its standard deviation. So this is the ratio of basically how great are the updates to the values in these tensors.

Then we're going to take a log of it. And actually I'd like to take a log 10 just so it's a nicer visualization. So we're going to be basically looking at the exponents of this division here. And then that item to pop out the float. And we're going to be keeping track of this for all the parameters and adding it to this UD tensor.

So now let me reinitialize and run a thousand iterations. We can look at the activations, the gradients, and the parameter gradients as we did before. But now I have one more plot here to introduce. And what's happening here is we're iterating over all the parameters, and I'm constraining it again like I did here to just the weights.

So the number of dimensions in these sensors is two. And then I'm basically plotting all of these update ratios over time. So when I plot this, I plot those ratios and you can see that they evolve over time during initialization to take on certain values. And then these updates are like start stabilizing usually during training.

Then the other thing that I'm plotting here is I'm plotting here like an approximate value that is a rough guide for what it roughly should be. And it should be like roughly 1 and -3. And so that means that basically there's some values in this tensor and they take on certain values and the updates to them at every single iteration are no more than roughly one thousandth of the actual magnitude in those tensors.

If this was much larger, like for example, if the log of this was like say -1, this is actually updating those values quite a lot. They're undergoing a lot of change. But the reason that the final layer here is an outlier is because this layer was artificially shrunk down to keep the softmax unconfident.

So here you see how we multiply the weight by 0.1 in the initialization to make the last layer prediction less confident. That artificially made the values inside that tensor way too low. And that's why we're getting temporarily a very high ratio. But you see that that stabilizes over time once that weight starts to learn.

But basically I like to look at the evolution of this update ratio for all my parameters usually and I like to make sure that it's not too much above 1 and -3 roughly. So around -3 on this log plot. If it's below -3, usually that means that the parameters are not training fast enough.

So if our learning rate was very low, let's do that experiment. Let's initialize and then let's actually do a learning rate of say 1 and -3 here. So 0.001. If your learning rate is way too low, this plot will typically reveal it. So you see how all of these updates are way too small.

So the size of the update is basically 10,000 times in magnitude to the size of the numbers in that tensor in the first place. So this is a symptom of training way too slow. So this is another way to sometimes set the learning rate and to get a sense of what that learning rate should be.

And ultimately this is something that you would keep track of. If anything, the learning rate here is a little bit on the higher side because you see that we're above the black line of -3. We're somewhere around -2.5. It's like okay. But everything is somewhat stabilizing and so this looks like a pretty decent setting of learning rates and so on.

But this is something to look at. And when things are miscalibrated, you will see very quickly. So for example, everything looks pretty well behaved, right? But just as a comparison, when things are not properly calibrated, what does that look like? Let me come up here and let's say that for example, what do we do?

Let's say that we forgot to apply this fan-in normalization. So the weights inside the linear layers are just a sample from a Gaussian in all those stages. What happens to our - how do we notice that something's off? Well the activation plot will tell you, whoa, your neurons are way too saturated.

The gradients are going to be all messed up. And the histogram for these weights are going to be all messed up as well. And there's a lot of asymmetry. And then if we look here, I suspect it's all going to be also pretty messed up. So you see there's a lot of discrepancy in how fast these layers are learning.

And some of them are learning way too fast. So -1, -1.5, those are very large numbers in terms of this ratio. Again, you should be somewhere around -3 and not much more above that. So this is how miscalibrations of your neural nets are going to manifest. And these kinds of plots here are a good way of sort of bringing those miscalibrations to your attention and so you can address them.

Okay, so so far we've seen that when we have this linear tanh sandwich, we can actually precisely calibrate the gains and make the activations, the gradients, and the parameters, and the updates all look pretty decent. But it definitely feels a little bit like balancing of a pencil on your finger.

And that's because this gain has to be very precisely calibrated. So now let's introduce batch normalization layers into the mix. Let's see how that helps fix the problem. So here, I'm going to take the BatchNorm1D class, and I'm going to start placing it inside. And as I mentioned before, the standard typical place you would place it is between the linear layer, so right after it, but before the nonlinearity.

But people have definitely played with that. And in fact, you can get very similar results, even if you place it after the nonlinearity. And the other thing that I wanted to mention is it's totally fine to also place it at the end, after the last linear layer and before the loss function.

So this is potentially fine as well. And in this case, this would be output, would be vocab size. Now because the last layer is BatchNorm, we would not be changing the weight to make the softmax less confident. We'd be changing the gamma. Because gamma, remember, in the BatchNorm, is the variable that multiplicatively interacts with the output of that normalization.

So we can initialize this sandwich now. We can train, and we can see that the activations are going to of course look very good. And they are going to necessarily look good, because now before every single tanh layer, there is a normalization in the BatchNorm. So this is unsurprisingly all looks pretty good.

It's going to be standard deviation of roughly 0.65, 2%, and roughly equal standard deviation throughout the entire layers. So everything looks very homogeneous. The gradients look good. The weights look good in their distributions. And then the updates also look pretty reasonable. We're going above -3 a little bit, but not by too much.

So all the parameters are training at roughly the same rate here. But now what we've gained is we are going to be slightly less brittle with respect to the gain of these. So for example, I can make the gain be, say, 0.2 here, which is much slower than what we had with the tanh.

But as we'll see, the activations will actually be exactly unaffected. And that's because of, again, this explicit normalization. The gradients are going to look okay. The weight gradients are going to look okay. But actually the updates will change. And so even though the forward and backward paths to a very large extent look okay, because of the backward paths of the Bash norm and how the scale of the incoming activations interacts in the Bash norm and its backward paths, this is actually changing the scale of the updates on these parameters.

So the gradients of these weights are affected. So we still don't get a completely free path to pass in arbitrary weights here, but everything else is significantly more robust in terms of the forward, backward, and the weight gradients. It's just that you may have to retune your learning rate if you are changing sufficiently the scale of the activations that are coming into the Bash norms.

So here, for example, we changed the gains of these linear layers to be greater, and we're seeing that the updates are coming out lower as a result. And then finally, if we are using Bash norms, we don't actually need to necessarily—let me reset this to 1 so there's no gain—we don't necessarily even have to normalize backfan_in sometimes.

So if I take out the fan_in, so these are just now random Gaussian, we'll see that because of Bash norm, this will actually be relatively well-behaved. So this will of course in the forward path look good. The gradients look good. The backward weight updates look okay. A little bit of fat tails on some of the layers, and this looks okay as well.

But as you can see, we're significantly below -3, so we'd have to bump up the learning rate of this Bash norm so that we are training more properly. And in particular, looking at this, roughly looks like we have to 10x the learning rate to get to about 1e-3. So we'd come here and we would change this to be update of 1.0.

And if I reinitialize, then we'll see that everything still of course looks good. And now we are roughly here, and we expect this to be an okay training run. So long story short, we are significantly more robust to the gain of these linear layers, whether or not we have to apply the fan_in.

And then we can change the gain, but we actually do have to worry a little bit about the update scales and making sure that the learning rate is properly calibrated here. But the activations of the forward, backward paths and the updates are looking significantly more well-behaved, except for the global scale that is potentially being adjusted here.

Okay, so now let me summarize. There are three things I was hoping to achieve with this section. Number one, I wanted to introduce you to Bash normalization, which is one of the first modern innovations that we're looking into that helped stabilize very deep neural networks and their training. And I hope you understand how the Bash normalization works and how it would be used in a neural network.

Number two, I was hoping to PyTorchify some of our code and wrap it up into these modules. So like linear, Bash normalization 1D, 10H, et cetera. These are layers or modules, and they can be stacked up into neural nets like Lego building blocks. And these layers actually exist in PyTorch.

And if you import torch-nn, then you can actually, the way I've constructed it, you can simply just use PyTorch by prepending nn. to all these different layers. And actually everything will just work because the API that I've developed here is identical to the API that PyTorch uses. And the implementation also is basically, as far as I'm aware, identical to the one in PyTorch.

And number three, I tried to introduce you to the diagnostic tools that you would use to understand whether your neural network is in a good state dynamically. So we are looking at the statistics and histograms and activation of the forward pass activations, the backward pass gradients. And then also we're looking at the weights that are going to be updated as part of stochastic gradient ascent.

And we're looking at their means, standard deviations, and also the ratio of gradients to data, or even better, the updates to data. And we saw that typically we don't actually look at it as a single snapshot frozen in time at some particular iteration. Typically people look at this as over time, just like I've done here.

And they look at these update to data ratios and they make sure everything looks okay. And in particular, I said that 1e-3, or basically negative 3 on the log scale, is a good rough heuristic for what you want this ratio to be. And if it's way too high, then probably the learning rate or the updates are a little too big.

And if it's way too small, then the learning rate is probably too small. So that's just some of the things that you may want to play with when you try to get your neural network to work very well. Now, there's a number of things I did not try to achieve.

I did not try to beat our previous performance, as an example, by introducing the BatchNorm layer. Actually, I did try, and I found that I used the learning rate finding mechanism that I've described before. I tried to train the BatchNorm layer, a BatchNorm neural net, and I actually ended up with results that are very, very similar to what we've obtained before.

And that's because our performance now is not bottlenecked by the optimization, which is what BatchNorm is helping with. The performance at this stage is bottlenecked by what I suspect is the context length of our context. So currently, we are taking three characters to predict the fourth one, and I think we need to go beyond that.

And we need to look at more powerful architectures, like recurrent neural networks and transformers, in order to further push the like probabilities that we're achieving on this dataset. And I also did not try to have a full explanation of all of these activations, the gradients and the backward pass, and the statistics of all these gradients.

And so you may have found some of the parts here unintuitive, and maybe you're slightly confused about, okay, if I change the gain here, how come that we need a different learning rate? But I didn't go into the full detail, because you'd have to actually look at the backward pass of all these different layers and get an intuitive understanding of how that works.

And I did not go into that in this lecture. The purpose really was just to introduce you to the diagnostic tools and what they look like. But there's still a lot of work remaining on the intuitive level to understand the initialization, the backward pass, and how all of that interacts.

But you shouldn't feel too bad, because honestly, we are getting to the cutting edge of where the field is. We certainly haven't, I would say, solved initialization, and we haven't solved backpropagation. And these are still very much an active area of research. People are still trying to figure out what is the best way to initialize these networks, what is the best update rule to use, and so on.

So none of this is really solved, and we don't really have all the answers to all these cases. But at least we're making progress, and at least we have some tools to tell us whether or not things are on the right track for now. So I think we've made positive progress in this lecture, and I hope you enjoyed that.

And I will see you next time.