[Paper Club] GMT20251112 200413 Recording gallery 3440x1440
00:00:00.560 | well yes i would but i was waiting for a screen share to start oh sorry it's okay slight editing
00:00:08.640 | um okay screen is sharing thing is recording uh so we have a few things that came out
00:00:18.240 | basically um i think what a week ago kimmy dropped kimmy uh linear it's it's just small different
00:00:27.520 | hybrid attention stuff ted will go over that in a bit and then this week came out kimmy k2 thinking
00:00:33.520 | it's basically an extension of kimmy k2 but it now has reasoning and thinking and it's pretty cool
00:00:39.440 | because it basically popped the benchmarks in in every stat so big big jump um it's open weight like
00:00:46.960 | before the the notable ones were on like humanity's last exam i'll give a quick high level overview before
00:00:54.560 | we kind of dive deep honestly this um this twitter post by artificial analysis is pretty good so open
00:01:01.840 | source uh they use int4 this time instead of fp8 so it's better quantized doubled the context length it's
00:01:09.280 | a lot more sparse um really good on humanities last exam similar to gpt oss it's now trained to do
00:01:17.040 | tool calls and reasoning and yeah it's kind of like very state-of-the-art it's still trillion parameters it's
00:01:22.400 | still huge um it's very very verbose though so there's two endpoints of fast and a regular but
00:01:29.360 | you know one thing that they note here that you wouldn't see is i think it's like the most expensive
00:01:33.840 | um most verbose tokens that communicate to thinking use the highest number of tokens ever used in their
00:01:40.800 | eval harness so their evil harness they basically test the model across all benchmarks uh it's nice that
00:01:46.800 | they actually shipped in for and they tested in for but you know it's very very verbose it thinks a lot
00:01:54.080 | but that being said it's still very good there's a heavy version of it that uses even more tokens
00:02:00.400 | and um yes even better uh on benchmarks you know it's it's very very state-of-the-art so like humanity's
00:02:07.280 | last exam beats gpt5 high beats growth for on other stuff it's it's pretty up there and on par um i of
00:02:15.200 | course use gpt5 to give a bit of a summary and i think it honestly does pretty well since there's no
00:02:21.680 | paper uh what's more interesting is actually there's some commentary like nathan from interconnects did a
00:02:28.480 | pretty good what are the five things that matter about it um someone posted something about their
00:02:34.640 | inference on reddit there's a little q a session about quantization so let's just dig in pretty fast so
00:02:42.000 | k2 thinking i don't know if anyone has thoughts they actually use it or whatnot uh the other aspect of
00:02:48.720 | this is it's their servers are super on fire so um they talk about the speeds that they get here um
00:02:58.800 | performance is good here's how it performs but basically um they reported it gets uh the the base
00:03:05.520 | endpoint is very slow getting about eight output tokens per second while turbo is slightly faster
00:03:10.080 | uh that's that's not the worst case right it's still open weights other providers will support it
00:03:16.320 | um so you know you it's slow but you know base 10 is doing it pretty fast and still pretty cheap
00:03:23.040 | um but you know will will many people use it who knows it's it's still mit license there's two clauses
00:03:28.960 | in there i think one is if you make more than 20 mil a month or you have like a bunch of users you want
00:03:34.240 | to prominently say you're using kimi k2 so yeah now it reasons it can plan tool call and stuff between its
00:03:43.280 | thinking it's trained with quantization aware training in int 4 and plus training we'll talk
00:03:49.680 | about that a bit later that really helps speed and rl they doubled the context length which is pretty
00:03:55.280 | exciting yeah it's it's quite state-of-the-art stuff uh some stuff is uh slightly behind but you know in
00:04:02.000 | general it's quite good it's like a little midpoint where open source was able to like take quite a win
00:04:07.520 | again um with it being int 4 compared to k2 we'll talk about quantization aware training and stuff uh
00:04:16.720 | someone's asking in the chat with it being um int 4 it it's you know the last k2 was fpa i believe
00:04:26.240 | so it's quantized basically to take half the memory so there's a deployment guide with vllm
00:04:33.280 | somewhere here deployment um basically now you can run it on a node it's optimized for older hardware
00:04:40.880 | it's it's not like fp4 um so you know cool stuff like that you it's basically a lot faster
00:04:47.280 | and better um here's the clause 100 million monthly active users or 20 million monthly revenue
00:04:52.720 | what else there's the official blog post which you can go through it's mostly just evals and hype
00:04:58.400 | there's not much here agentic reasoning oh my mouse is frozen okay we're good we're good um what else
00:05:07.360 | api is there it's slow on kimmy but you know other people have it uh it builds a lot on the old k2
00:05:14.320 | it's more sparse deployment guide let's see what else what else yeah uh it can reason and tool call a lot
00:05:21.440 | between 200 to 300 sequential tool calls int 4 versus quantize uh through quantize aware training
00:05:29.760 | we'll talk about that through the reddit post in a bit longer context um with this similar to how
00:05:35.760 | openai had harmony they open source for gpt oss uh you want to make sure that you follow their um
00:05:42.480 | their format parsing so you can actually properly parse these tool calls there's like a whole section
00:05:48.080 | on this i don't know if anyone here is actually renting a node to deploy it most of us will just
00:05:52.800 | consume and use apis and you know that's that's pretty much the norm right now uh architecture wise
00:05:58.800 | still a trillion parameters it's 32p active uh 384 experts top eight one shared expert uh context length
00:06:06.800 | has doubled so you know 32 be active this thing can get fast it's just that i'm sure kimmy servers are
00:06:12.400 | like quite cooked and on fire right now a sparse in this context so there's a sparsity ratio so the
00:06:18.880 | number of active versus total experts right um this is something that kimmy has really been pushing
00:06:25.440 | is the sparsity ratio going down or is it going up i thought it's more sparse than before am i mistaken
00:06:32.000 | in this uh we'll we'll double check that in a sec but i thought it's i thought it's more sparse than
00:06:38.400 | before but we'll we'll double see maybe someone else can check uh benchmarks i don't know if there's
00:06:43.680 | much of a point in looking in benchmarks the interesting thing to note is that there is a heavy
00:06:47.760 | equivalent um benchmarks on hugging face are laid out quite well honestly like depending on what you
00:06:55.280 | care about one i don't know if many people are actually going to end up using it it is quite a bit
00:07:00.080 | cheaper but um you know if you care about humanity's last exams it's pretty state-of-the-art artificial
00:07:06.720 | analysis has their aggregated benchmark which still shows that like you know right there after open ai
00:07:12.400 | the only things to be aware of that don't show up in benchmarks is that it is very very verbose so
00:07:19.840 | uses a lot a lot of tokens to think and that's that's not optimal how to use it we don't need to know
00:07:26.320 | any of this uh design and training notes so moe with mla very sparse moe keep stop active 32 it
00:07:35.600 | still uses me on clip they didn't they didn't share that much more in for uh quantized aware training
00:07:40.800 | they talk about this a bit in the system report and read it we'll go over there they have caching they
00:07:46.560 | have standard they have a turbo okay i think that's enough of a high level of what came out uh nathan
00:07:52.960 | from interconnects put out you know a pretty good post about how their releases come out from um
00:08:00.800 | chinese labs benchmarks first user behavior second china on the rise so basically release stuff uh after
00:08:09.040 | they see people in the us doing it uh this is new it's like you know the interleave thinking with tool
00:08:14.640 | calls it's really good for agents this is kind of like not many open models did this except for gpt oss so
00:08:20.960 | it's the first one after that i think uh pressure on american labs of course i don't think there's
00:08:26.880 | too much more to go over through artificial analysis um okay so what is this whole quantization is a comp
00:08:33.760 | is not a compromise it's the next paradigm so an infra engineer shares insights on why this choice matters
00:08:41.280 | uh key idea quantization is no longer a trade-off it's it's actually more beneficial so there's there's in
00:08:48.720 | traditional inference there's two reasons why there's two goals of optimization right high throughput so
00:08:54.240 | as you quantize you can get better utilization of your gpu right this mattered a lot for early like
00:09:00.000 | dense models on local hardware whether you have a mac or like a 30 90 40 90 50 90 you could do uh you
00:09:07.520 | know four bit quant on a 32b fit it in ram and use it and then of course lower latency um if you know
00:09:16.240 | the more quantized it is the lower latency you can get so for their thing um with such a sparse moe
00:09:24.320 | their decoding is actually memory bound the smaller the model weights uh the faster the compute is so in
00:09:31.360 | previous their fp8 where they had about it took about a terabyte of memory right they were at the
00:09:36.960 | limit of what single high speed interconnect per gpu node can can handle now they have um weights at four
00:09:45.040 | bit activations at 16 bit it's a interesting type of quantization it slightly uh latency drops quite a bit
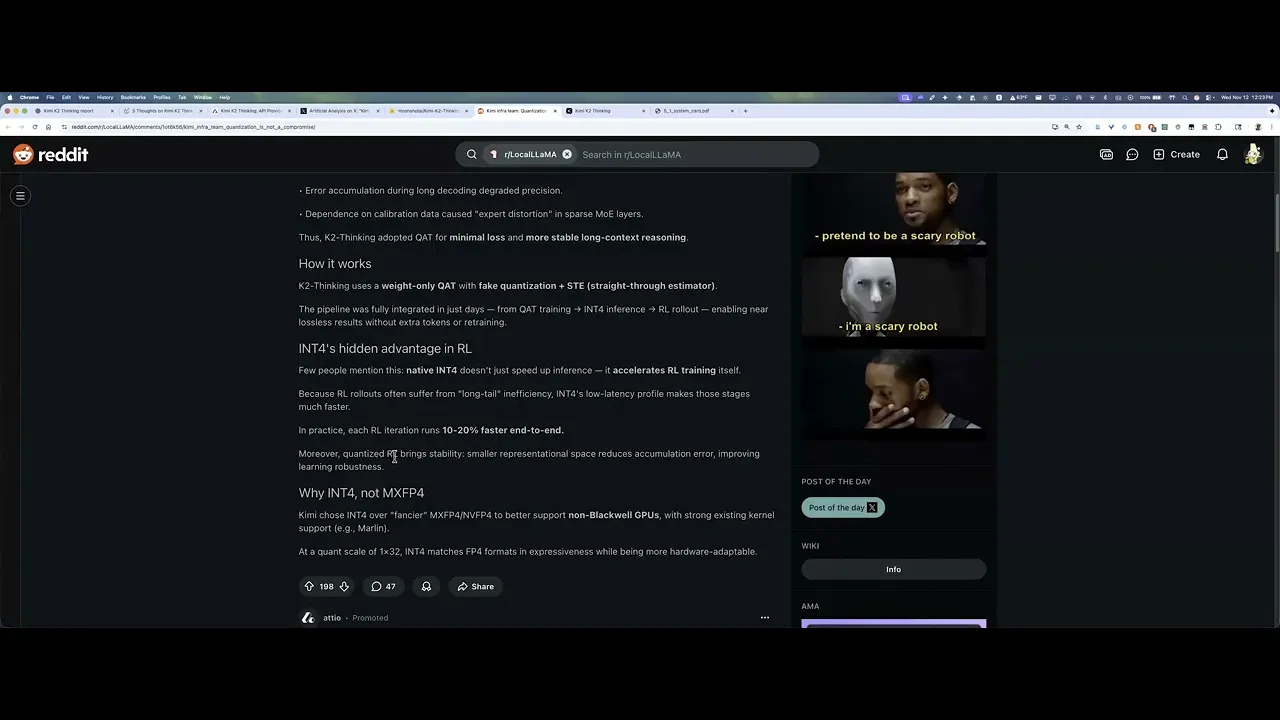
00:09:53.760 | and it maintains quality and it's in a sense lossless so why uh quantize aware training over post training
00:10:00.720 | quantization uh post training worked fine for shorter generations but it didn't work in long chain so
00:10:06.880 | another big thing another big thing that they did here is one they doubled the context two they do um
00:10:12.160 | tool call reasoning right so this thing is very verbose it's more verbose in thinking than any other
00:10:18.800 | model it does tool calls interleaved in its thinking and yeah uh post training quantization didn't work
00:10:26.960 | errors basically accumulated and then it degraded precision over long contexts but um quantize aware
00:10:34.560 | training didn't do it so how does it work uh dependence on calibration expertise this was these
00:10:40.480 | are issues with post trading quantization k2 k2 thinking adopted quantize aware training for minimal
00:10:46.320 | loss and more stable long context reasoning how it works it uses a weight only quantize aware training
00:10:52.400 | and a fake quantization plus straight through estimator um little details here it four is the hidden
00:10:59.280 | advantage in rl a few people mentioned this this is kind of what all the blog posts and tweets about it
00:11:04.880 | show uh it for doesn't just speed up inference it accelerates rl training itself right if you think
00:11:11.280 | about rl and all this verification you have a lot of rollouts being done and you know if you can speed
00:11:17.840 | those up you're essentially accelerating all your rl in general too right rl rollouts suffer from long-term
00:11:24.800 | inefficiency but this low latency profile makes it much faster and you probably have uh less overhead
00:11:31.840 | where you're off policy per se as rollouts are sinking and new weights are being updated uh this
00:11:37.600 | is pretty interesting right so uh once again the title of this is quantization is not a compromise
00:11:42.640 | it's the next paradigm um they they basically say in practice each rl iteration runs 10 to 20 percent
00:11:51.200 | faster end to end with this in for um with this in for quantize aware training uh moreover quantized
00:11:59.760 | rl brings stability smaller representational space reduces accumulation error improving learning robustness
00:12:05.600 | so why in for versus uh mx fp4 any of these other fancy fancier quantization stuff uh basically all
00:12:14.640 | this new fancy stuff like fp4 it it's new to blackwell but it won't work with older hardware so uh more
00:12:24.080 | generalization is what it for gives you it for can work across older hardware and you know that's a trade
00:12:29.680 | off they're they're willing to make so at uh quant scale of 1 to 32 it for matches fp4 formats it's
00:12:37.760 | like you know it's more hardware adaptable even though it's not the latest fancy stuff because it works
00:12:43.200 | not non uh blackwell okay that's like quick 10 to 15 minute overview of k2 thinking i'll pause here for
00:12:53.840 | questions questions comments i see chat is quite active i honestly haven't had a chance to look through
00:12:59.520 | it if anyone wants to you know interrupt or go over any parts in specific detail feel free you know
00:13:06.400 | i'm gonna go through chat but feel free to unmute or whatever or we can always pass to ted and then do
00:13:12.240 | do q a towards the end and keep it in in zoom
00:13:20.720 | import restrictions force for creativity yeah a lot of people say that um the chinese labs do really
00:13:26.000 | good stuff like uh muon clip a lot of deep seeks um innovations were basically because they don't
00:13:32.240 | have the best gpus so they're forced to get creative and yeah um how many 50 90s do you need to run
00:13:40.320 | this you need a lot of 50 90s you need you need the pewdiepie rig you need chinese 48 gig 50 90s or you
00:13:47.680 | know there's always the a6000 pro the a6000 rtx it's it's where you pay twice as much for more vram you
00:13:55.760 | get a 50 90 level performance with 96 gigs of arab you put four or six of those in a box and you can run
00:14:02.880 | this thing locally and it'll be slow or you could always just you know use the cloud where this thing is
00:14:09.440 | like two dollars on the millions of tokens but the uh the kimmy lin here that's what 48 48 billion
00:14:18.640 | parameter if i'm not mistaken so there's a version of that you can run yeah but it's it's more of an
00:14:23.120 | experimental it's not really a stated yard model yet yeah
00:14:30.000 | quirks is if you ask it for code it will generate code and thinking see if it's correct and produce
00:14:36.000 | the same main output i think ankit is uh making an interesting point here i think you can't look at
00:14:43.280 | thinking tokens as uh quirks thinking tokens are all basically like random random latent space noise like
00:14:53.840 | models even deep sea kimmy um all of them will basically do random stuff in their thinking
00:14:59.840 | those switch languages they'll write code for poetry they'll do poetry for code and then they'll output a
00:15:05.440 | really reasonable answer so um you know they make it a pretty clear point that there's a reason why you
00:15:10.960 | don't output your um chain of thought reasoning to the end user like people were salty at opening
00:15:18.960 | eyes first 01 model for not giving chain of thought tokens but in reality what we see now is you know
00:15:25.360 | there's so much noise in there like summarizing it is probably the better ux right you don't want to
00:15:30.240 | ask it for code and get a bunch of um you don't want to get like poetry in your code thinking it doesn't
00:15:36.240 | really help um let's see any other questions otherwise i will probably pass over to ted and
00:15:42.240 | i'll keep i'll keep answering in the zoom chat but yeah it's better than minimax um trade-offs are there
00:15:50.400 | they don't really talk about anything locally it will be 10 tokens per second no it'll probably be
00:15:55.280 | worse than 10 tokens per second right now the kimmy servers are serving it at eight tokens per second so
00:16:02.640 | 10 tokens per second would be great on your 5090 but no these things are things are pretty raw
00:16:07.840 | okay i think um a quick question so you mentioned a 10 to 20 percent uh increase end-to-end on ril
00:16:18.720 | training right uh that doesn't seem to be a very large number um and i was wondering like is this speed up
00:16:25.840 | any other thing else on this article is about the uh bandwidth limit right so can we kind of correlate
00:16:33.760 | those two things like um you know that you're going when you went to int for and uh how much
00:16:39.680 | more bandwidth are you allowed now uh for gpu transfer and then how does that correlate with the speed
00:16:46.080 | yeah i think there's a high level map that you can work through right so quantization will be faster
00:16:52.240 | uh you're also taking half the ram so you know if you have x amount of gpus there's actually a
00:16:57.920 | a full breakdown of this somewhere i can share a link at some point in the zoom chat um but yeah you
00:17:04.800 | break down the factors that you have right so you have faster you have half the vram required so they
00:17:09.280 | they did a scaling compared to chinchilla somewhere um but in my opinion 10 to 20 percent is uh it's quite a
00:17:15.760 | bit right if you compound it out for your experiments plus your final train run like the final train run
00:17:22.080 | to train a million token a trillion parameter model is in the millions of dollars right so if you're 20
00:17:31.040 | faster uh you can use 20 less gpu hours per se right so that's pretty substantial uh i don't i don't know
00:17:41.360 | if that's exactly a fair way to put it but 10 to 20 speedups are pretty uncommon right um just yeah i
00:17:50.160 | think that alone is pretty impactful but then when you think about it you know um it's it's very rollout
00:17:55.600 | heavy and if you look at what the actual bottlenecks were from um bandwidth across uh their parallel is uh
00:18:04.640 | their pipeline parallelism and gpu sharding um having more on less gpus it really helps break
00:18:12.720 | that down i i feel like i saw a good post about this i'll try to find it and share it oh yeah you could
00:18:18.560 | spend more i think uh it's not just about spending more though right this this uh this optimization is
00:18:24.400 | also at inference time so you'll you should see speed ups during brain and plane inference and forget about
00:18:33.360 | other providers like the whole one of the big benefits about open models and open weights is
00:18:38.560 | you can serve them yourself right you want to use k2 you need to find a terabyte of your app you
00:18:43.760 | want to use k2 thinking you can do it on half the half the memory so that alone is a lot better than
00:18:49.840 | a 10 10 to 20 speed up right it's it's also after gpu is required and then the other thing that they
00:18:56.560 | mention is that you went to int 4 making uh rl training more robust um and just that end sentence
00:19:03.760 | on that section i don't quite understand why that would be says oh smaller representative space reduce
00:19:09.040 | accumulation error or why is that uh it seems like you're more quantized so it doesn't that you know
00:19:15.360 | accumulate even worse so what is this reasoning there i think someone talked about it in the comments here
00:19:23.440 | magic just having a robust quantization now that's during compute there's there's an answer that
00:19:29.280 | someone gave about it i'll share it in the chat a bit but um i think we should as a separate thing i i
00:19:36.320 | remember reading somewhere an analysis that said that rl updates tend to be like rank one
00:19:41.840 | so int 4 shouldn't be a problem at all for rl if it works for for regular training it'll definitely
00:19:50.080 | work for rl yeah so i don't know if you answered your question frankie maybe it's just it's faster
00:19:56.560 | and it's just as good okay it brings stability smaller representational spit uh space reduces accumulation
00:20:06.160 | error improving learning robustness i'm sure there's more we can dig into here
00:20:10.240 | but um it's a fair question i feel like we should yeah the quantization aware maybe is what they're
00:20:15.760 | saying makes it better yeah versus um you know post that strange motivation okay i hope i didn't take
00:20:25.040 | up too much of your time ted there wasn't that much in this one no that was great so uh let me talk about
00:20:31.840 | the kimmy linear paper uh share my screen uh i'm always impressed with how much information viibu can
00:20:43.200 | cover um so fast so uh i don't know that i can i can i can match that but so we have this kimmy linear
00:20:51.040 | paper let me just do the quick highlights so it's a hybrid linear attention architecture so it's going to be
00:20:57.040 | one quarter of the layers are regular attention and and three quarters of the layers are going to be
00:21:01.840 | their new kimmy linear thing okay and there can be a linear thing they call kimmy delta attention kda
00:21:07.760 | so we'll get into it but they say it's an expressive linear attention module that extends gated delta net
00:21:14.480 | with a finer finer grain gating mechanism and then they have um a bespoke chunk wise algorithm that achieves
00:21:22.560 | high hardware efficiency so so um talk about that too remind me if i don't but that's an important
00:21:28.320 | element for any linear model um so they pre-trained this 3 billion active 48 billion total so this is
00:21:36.480 | this is not quite like state-of-the-art size and i think some of the experiments in the paper were done
00:21:41.920 | even smaller so um just know that this is this is like a proof of concept maybe more than it is the
00:21:49.040 | model you're going to start using daily but the key thing is because the linear has so much less memory
00:21:55.200 | requirements if only a quarter of the layers are regular attention then you're reducing your kv cache
00:22:01.040 | size by 75 percent and that's like you know if vbo's saying 10 20 is a pretty good increase 75 is is a
00:22:09.360 | very notable decrease in your memory utilization they have some decoding throughput numbers i i didn't
00:22:16.080 | understand they have some graphs that differ but it's like 2.9x 3x 6x um but basically um because decoding
00:22:25.920 | is memory bound um bandwidth bound then when you reduce the kv cache by by three quarters that of
00:22:34.960 | course speeds up your decoding and that's where that speed up comes from whatever the exact number is
00:22:39.200 | and the cool thing is they open source the kda kernel and the vlm implementation
00:22:47.360 | okay so um let me jump ahead to what this uh what this model looks like okay so they have uh layers
00:23:02.720 | where they do kda instead of regular attention and then they have layers where they do regular attention
00:23:07.760 | and you know tldr in the end they're going to say we did relations and we found that three of these
00:23:13.040 | for every one normal one gave us the best bang for our buck um the the attention layers are using
00:23:21.520 | latent attention like deep seek uh but that's not particularly noteworthy um it's a mixture of
00:23:27.200 | experts model and the moe is just completely standard um so i feel like the really interesting thing to talk
00:23:34.640 | about can be linear is their new um kda um uh layer that that's replacing the attention and it's doing
00:23:43.120 | sort of a uh uh local attention it's not it's not there to be able to do um you know in context uh
00:23:54.320 | retrieval of a token that's you know 10 000 100 000 tokens ago that's what the one quarter of the layers
00:24:01.600 | that are full attention are there for but if you just need something like the previous token
00:24:06.320 | two tokens ago um then this guy is is going to take care of it for you and it's actually really strong
00:24:13.040 | and it can do more than that um all right so i'm trying to follow the chat but you guys are typing
00:24:20.160 | faster than every time i look at it so shout out if there's anything uh um that i'm going too fast
00:24:27.520 | you want me to to answer or whatever all right so i thought that if what we're going to focus on is
00:24:32.960 | just this kda thing then it actually makes sense to start with their related work section um down in
00:24:39.680 | section seven and then we'll get into the details and i think we'll have just enough time to talk a
00:24:44.160 | little bit about the the math okay so it starts with linear attention and um the idea is that attention i
00:24:52.720 | think you guys know quadratic so it reformulates the quadratic attention map into kernelized feature
00:24:57.760 | interactions replacing the soft max with a positive feature map so that tension can be computed through
00:25:03.280 | two associative matrix products uh this is a little bit like the kernel trick that you see in svms which
00:25:10.000 | can take something non-linear and turn it into something linearly separable so ultimately you don't
00:25:15.680 | necessarily really need to know that but um so you get rid of this explicit um um quadratic uh attention
00:25:24.720 | similarity matrix because you you you hope for it learning some pattern that that this kernel makes
00:25:31.440 | linearly separable and so then we just have uh uh linear uh calculations uh and then let's see here
00:25:38.320 | subsequent work strengthens the vanilla linear attention significantly through uh more refined memory
00:25:43.680 | control shifting from data independent decay it's more adaptive data dependent mechanisms so for example
00:25:50.400 | mamba just uh had this um decay thing and then mamba 2 they introduced where the decay was a function
00:25:59.680 | of what the current token is so that's what they mean when they say data dependent decay mechanisms
00:26:06.000 | and i'll talk more about how this decay stuff works um and refining the decay granularity from course
00:26:12.000 | headwise to precise channel wise decay so that's one of the big things here is that they're actually
00:26:17.440 | going to say my model dimension is 2048 instead of just decaying all 2040 of those floats by the same
00:26:25.520 | factor 0.9 i'm actually going to choose channel wise which ones i'm going to keep which ones i'm going to
00:26:31.680 | decay um so gated linear attention generalizes these approaches with diagonal channel wise gates so that's the decay
00:26:39.680 | thing table seven summaries collectively these men methods cast attention as compact recurrent memory
00:26:46.960 | updated with parallel prefix scan operators infused matrix multiplies aligning with modern accelerators
00:26:53.600 | that's a whole mouthful basically um what linear attention and kda and mamba and rwkb and gated delta net all of these
00:27:05.200 | things what they have in common is that at decode time they act like an rnn so you push one thing in
00:27:12.320 | it updates the state you get one thing out that's not enough in order to have a good linear attention
00:27:19.280 | you need three things you need the the easy one which is that decoding goes um uh really easily and really
00:27:27.600 | fast the second thing you need is that training and or pre-fill is done really fast and that's where
00:27:36.400 | you see this business of parallel prefix scans fused matrix multiply what they have in here this chunked
00:27:43.200 | operator that's the thing that does the prefix the pre-fill operation really fast or the training operation
00:27:50.880 | really fast otherwise if you just had a vanilla rnn and you give it a big amount of code and you have
00:27:58.240 | a hundred thousand tokens it would need to process those hundred thousand sequentially and it'd be really
00:28:03.120 | slow the decoding tokens per second would be really fast but the pre-fill would suck so you need those two
00:28:09.120 | things you need fast pre-fill you need fast decode and then the third thing you need is you need the
00:28:14.080 | attention to actually um uh be really smart be able to to um learn very complex patterns so what i'm mostly
00:28:22.720 | going to talk about is this complementary view of the same linear tension connects um linear tension to
00:28:29.600 | this idea of fast weight memory um and the state is a low capacity associated table and so that's that's
00:28:36.880 | the view that i find most intuitive for understanding these things um so then they also talk about linear
00:28:42.560 | tension with the gating mechanism and it's really the same idea here and they say a primary distinction
00:28:49.120 | yeah sorry someone had a question that i think is uh in the right time they asked if you can go into the
00:28:54.960 | pre-fill a little bit more but why make mixes what makes pre-fill so fast and in general what pre-filling
00:29:02.560 | is so um so when we train models uh typically what we do is let's talk about early pre-training um so you
00:29:12.400 | start with a context length of say four thousand you present all four thousand you have teacher forcing
00:29:17.360 | which means that um no matter what the model predicts you're always just putting in the four thousand
00:29:22.320 | tokens from your original ground truth corpus and then you calculate cross entropy loss uh in parallel
00:29:29.040 | across all four thousand token positions you're really doing the same thing in pre-fill so if
00:29:34.480 | somebody has a very short question like what is the capital of france this is no big deal it's like eight
00:29:39.680 | tokens whether you did them in parallel you give them sequentially no biggie but when i uh am working
00:29:45.040 | on code and i and i give you um uh the files and let's say you need all of these files this 100 000 tokens
00:29:53.040 | then in order to start decoding and whether you're thinking whether you do tools whatever you're doing
00:29:59.440 | if you're going to start decoding you first need to process all 100 000 of these um and we've come to name
00:30:07.280 | this portion of the process pre-fill because its characteristics are very different from the one
00:30:13.040 | token at a time decoding that happens after that so under pre-fill we have all the data we have all
00:30:19.120 | the hundred thousand we don't care about any of the predictions so we can we can do this in a highly
00:30:24.240 | parallelist fashion and for regular attention um you can you can do this super parallel all at once
00:30:31.680 | and your gpus will be compute bound because they're doing so many matrix multiplies calculating your
00:30:37.920 | your keys queries multiplying them together all that stuff okay um as well as the mlps uh during decoding
00:30:45.840 | you only get one new token one new query um and you're multiplying that against all your node keys
00:30:52.240 | and then calculating attention and so it ends up that once your context gets long the the keys and values
00:31:00.320 | that you're loading into the gpu are more memory bandwidth limited than the amount of compute you
00:31:08.000 | actually need to do the matrix multiplies actually relatively fast and tiny and so um linear if you
00:31:16.320 | imagine just a regular old-fashioned rnn um it's really great because you just have this small state
00:31:21.360 | you put in one token and you do a little bit of operations and you get out the next token so they're
00:31:26.000 | really great for decoding but there is no in an old-fashioned rnn there is no way to do pre-fill
00:31:33.520 | in parallel you would have to just do them one at a time and if i give you a code base it's 100 000 tokens
00:31:39.440 | you're kind of screwed so everybody has to if you want to have a competitive rnn style linear mechanism
00:31:47.360 | which will save on memory you also need to have a second mode where you can in parallel process
00:31:55.040 | these hundred thousand tokens not one at a time there has to be some trick and so this chunked method
00:32:00.880 | um in the kda paper and then similar in other papers uh mamba whatever they they have some some way of
00:32:08.160 | transforming the math to say there's an equivalence if i do it this way i get the same answer in parallel
00:32:14.000 | versus having to process every token one at a time did that for whoever had that it already scrolled off
00:32:21.600 | my screen that answers the question all right cool thank you um all right so let me just read this
00:32:32.080 | real quick uh the primary distinction amongst various gated linear attention mechanism lies in the
00:32:38.160 | parameterization of the forget gate so we haven't talked about this yet so maybe reading this first
00:32:43.760 | it's a little bit out of order uh for instance retinet uses a data independent scalar decay alpha
00:32:50.240 | and mama2 employs data dependence scalar um specifically gated linear tension uses a diagonalized fine grade matrix
00:32:58.880 | um offering an effective trade-off between uh efficiency and performance and that's what we're going to get into
00:33:05.120 | here note also that aside from linear attention another way you can speed things up is you can do sparse
00:33:11.200 | attention so if we talk about the new um deep seek i don't even know what it's called but the new deep seek
00:33:17.440 | attention thing they're kind of doing a sparse kind of a thing where um uh they're not looking at all of the
00:33:26.640 | the tokens at once to calculate uh the attention but this paper is a linear form so i'm just gonna kind of focus on that
00:33:33.760 | all right any questions if not then i was thinking i would jump into um uh the the actual linear attention stuff
00:33:54.480 | all right so section 2.2 is the key section for understanding what they did in kda and um they
00:34:02.960 | didn't actually say this um because they have these different sections here what the heck are they
00:34:07.760 | doing what they're actually doing is they're they're doing a history of linear attention and they're
00:34:13.040 | building up from the simplest to the most complex and their latest thing which is kidney delta tension okay
00:34:21.440 | so section 2.2 none of this stuff literally is used in kda this is all the the history that builds up to
00:34:29.440 | we built our our kda by making a a slight tweak on on the last thing here
00:34:35.120 | so um to start with we're going to look at this first equation but this is just a basic linear attention
00:34:42.400 | and what i was thinking i would do is i would just like scribble a little bit so you guys can sort of
00:34:47.840 | understand the idea of the the associative memory so let me see if um do we have whiteboards turned on
00:34:58.320 | here is there something i can enable uh it might not be enabled during the meeting so no i don't see it
00:35:13.680 | okay okay this is this is new this is fancy this is everyone drawing all right people don't draw on
00:35:30.080 | this because i need to draw on this if you want if you want me to show you something you need to stop
00:35:33.680 | messing around okay um all right how do i erase it all right thanks guys
00:35:44.320 | um okay okay awesome so so let's start with just a regular kv cache okay and and it looks something
00:35:54.400 | like this
00:35:59.040 | all right so oh i just lost the whiteboard i think that was me i i thought i xed out of it for myself
00:36:10.640 | but i i did it for everybody apparently sorry that's okay i can never
00:36:14.880 | uh i can do it i think that you should be able to start a new whiteboard yeah yeah yeah yeah sorry
00:36:21.440 | all right nobody nobody mess with it all right all right do you guys see or do i need to share my
00:36:25.760 | screen we see it we see it okay all right so so let's start with a um a regular kv cache
00:36:36.080 | and if i can do this really quickly okay it looks something like this and basically um this here sorry
00:36:46.480 | i'm trying to do this fast this here is um is our sequence length
00:36:53.680 | okay and over here we're going to have our um our key dimension i'll call it d sub k
00:37:06.560 | and we're going to have our value dimension d sub v all right so so hopefully this looks familiar
00:37:13.920 | to you guys you have keys and values and it's as long as a single place and so basically um
00:37:19.200 | what you do in here is for every token that you've ever seen you store a copy of the the key and value
00:37:26.960 | after you've taken that token and run it through the embedding matrix w sub k w sub v all right and
00:37:32.800 | then you don't have to store these you could just recompute them and that's what the the sort of
00:37:37.200 | original attention thinking is but it's actually better if you think of it in terms of the kv cash
00:37:44.000 | all right so now what what what happens when we train the model is we learn different patterns that we care
00:37:51.280 | about and we have the ability to recall them on demand so let's say the llm wants to know if the current
00:37:58.480 | token is a noun okay then what it could do is it could have one of the head keys put a one in a
00:38:05.920 | certain place if the current token is a noun then if the query also has a one in that place then when
00:38:14.640 | you dot the query in the key your dot product is a is a large value you get a one and you're basically
00:38:20.080 | going to recall that so imagine that uh for simplicity now this is well okay let me just start
00:38:28.480 | this way so imagine that you just basically divided up your keys okay and you basically said hey i'm
00:38:34.800 | gonna put um a one here anytime it's a noun and i'm gonna put uh a one here anytime it's a verb
00:38:42.560 | okay so that's a way in which you could build this this key value memory and then anytime
00:38:50.400 | the head wants to match on prior words that are nouns you just pass in a query that looks like one zero zero
00:38:57.760 | zero zero whatever okay and then every word that's not a noun is going to have zeros here
00:39:02.640 | and so any word that's not a noun is going to have a very low value is going to have a zero value
00:39:07.760 | and so you're only going to get matches on nouns and then if everything is a zero except for verbs
00:39:13.040 | then you put in zero one zero zero zero as your query and you're going to get all the verbs now
00:39:17.920 | obviously you can design whatever you can learn whatever pattern you want okay but this is the
00:39:21.920 | idea so what this means is now we've built an associative memory okay so a regular array in
00:39:30.080 | python you you access it by index you say i want index 23 but here you can say i want nouns and you
00:39:37.200 | don't need to know what position they're in and you don't need to know how many there are you just
00:39:41.360 | simply say if my query is one zero zero zero zero i will get all nouns and if there's only one noun
00:39:48.400 | then if you say give me one zero zero you will get that exact uh right entry
00:39:53.440 | okay so the problem we have where it gets expensive is that in this formulation every time you decode and
00:40:04.240 | you get a new token you need to lengthen this sucker and so then you're basically adding another another
00:40:10.320 | column here and then you do decoding and you're adding another column here and this thing this thing
00:40:15.680 | just keeps growing uh in size and i and i it's not fancy my my columns lines aren't lining up but i but
00:40:23.920 | you get the gist so then by the time you get to hundred thousand tokens this thing is very large it's
00:40:28.320 | it's hundred thousand so the the promise of linear attention is let's not have this thing grow like crazy
00:40:36.240 | let's assign a fixed amount of memory to it and so if you said i'm going to assign um a fixed size of
00:40:46.480 | 1024 to this thing for the first 1024 tokens you're great right um or the first 1024 concepts that you want
00:40:58.000 | to store in here um you can basically just have a one you know um in the first row for the first thing
00:41:05.280 | and a one in the second row and you can just one hot and code it okay but what happens when you get to
00:41:11.200 | the next one the 1025th if your update rule um
00:41:19.840 | it is simply sort of something along the lines of uh of cycle through these one hot encodings
00:41:25.840 | and then you get to 1024 you're going to be back to a one in the first position and you're going to end
00:41:30.480 | up uh um uh writing something in here that's going to collide with this thing that you already had in
00:41:37.440 | there and so so this is where in the literature you'll see some stuff about collisions okay now the
00:41:43.120 | next thing we're going to do is we're going to so so we have to find a way to solve that um and so
00:41:48.080 | what you could do is you could say i'm going to erase this entry um with the with the one in the first
00:41:54.480 | row and then that'll create room for my 1025th thing so ultimately what you have to do is you have
00:41:59.920 | to have a rule that says what am i going to erase when i want to put something in and so that's where
00:42:05.680 | as you get to these more complicated linear models people are are having these decay rules these
00:42:12.800 | are the the the erase rules for for when do i get rid of stuff in my now very limited fixed sized kb
00:42:21.280 | cache okay so then the next thing we're going to do is we're going to do a little bit of linear algebra
00:42:26.880 | okay and so um if you if you recall in linear algebra um yes i could put a one in the first row one
00:42:36.320 | in the second row and this will give me this nice orthogonal basis in this case they'll also be length one
00:42:41.600 | so it'll be orthonormal and that's the the principal basis the one that you know is easy on the eyes
00:42:47.280 | but if this thing is d dimensional um i can have any d um orthogonal vectors and they will work perfectly
00:42:57.440 | well they do not have to be all one and all zeros um this first vector could be one one one one one and
00:43:04.240 | then the next one as long as it it's orthogonal to that first one um it could it could be anything and
00:43:10.720 | so that's where if you look at the keys in an lm you're not going to see one zero zero zero zero one
00:43:15.680 | zero zero but in fact they very well may be orthogonal to each other okay and we benefit from this concept
00:43:23.760 | that in high dimensionality the cursive dimensionality all random vectors are very close to orthogonal to
00:43:31.120 | each other so the dot product of two random vectors is likely to have a value close to zero all right and
00:43:38.480 | so um so in fact we don't use one zero zero zero we just use learn uh vectors okay so um so then the next
00:43:48.720 | first thing to understand is if we go back to i i think i can toggle back and forth but uh hold on a
00:43:57.280 | second where's my zoom menu here uh sharing will close the whiteboard uh okay i didn't want to do that
00:44:09.200 | hold on let me see if i can do this
00:44:18.160 | okay so this is the equation that's at the top of section 2.2 okay it says that here's my hidden state
00:44:28.800 | so so this is going to be my my new rectangle here okay and we initialize it with all zeros and um
00:44:37.120 | what we do is we when we process the first token we add in this thing k times v transpose so this is
00:44:45.840 | an outer product so if you're used to seeing dot products k transpose times v would be a scalar
00:44:52.240 | quantity okay but k times v transpose is going to give us a rank one and if k and v are our same
00:45:00.080 | dimensionality a rank one square matrix all right um and then it says
00:45:07.040 | the way that you you get your output so equivalent to your your soft max tension is um you you take
00:45:14.800 | the transpose of this matrix and you multiply it by your query so i want to just show you super quickly
00:45:19.840 | how this um ends up being a really clean associative memory so i'm going to drop the the t subs subscripts
00:45:29.760 | and and just do um uh uh uh one time step okay so we start with s is all zeros and then we say the first s
00:45:40.720 | equals uh k times uh v v transpose
00:45:52.400 | all right all right um then um how do we read the output from that so the output is we say it's s
00:46:03.360 | transpose times the query so what i'm going to do is i'm going to rewrite s using the equation up above
00:46:14.080 | and i'm going to transpose it so when i transpose it i'm going to get v times one second um uh k transpose
00:46:24.080 | if you know you know how your transpose matrix multiply works um times the query
00:46:33.840 | but but we can change the parentheses uh because matrix multiplies associative and so i can actually say
00:46:41.680 | this is v times k transpose times
00:46:47.040 | times the query okay and so in if if you are familiar with the softmax attention uh formula you
00:47:06.960 | you have this this k transpose times query thing i think it's written the other way around q query
00:47:13.040 | transpose times key whatever but you're multiplying your queries and your keys and then ultimately you're
00:47:17.760 | multiplying that by your values and then it's got a scaling thing square root of d blah blah blah whatever
00:47:22.720 | but so in this formulation we've basically got the same functionality as um we've got this query times
00:47:30.960 | key business just like in regular softmax attention and so uh i'm gonna try and go a little bit fast
00:47:37.600 | here just for the sake of time but hopefully this gives you at least a little bit of intuition that um
00:47:42.800 | that we can store these things and and we can recall them and it's performing something very similar to
00:47:51.840 | regular attention okay so the difference is that in our in our uh in our linear attention we don't have
00:47:59.200 | these two boxes okay we now just have one box and this is this is initialized to zeros and then when
00:48:08.000 | we get the first key in value we do this outer product it gives us a rank one square matrix and we
00:48:13.280 | sum it in here and so it's just going to be zero plus that it's going to be our original one the key
00:48:18.160 | thing from linear algebra is that if the second key is orthogonal to the first key and you and you do this
00:48:26.240 | thing again regardless of what the value is and you take that rank one matrix and you add it in here
00:48:32.480 | you will then get a rank two matrix and when you multiply by either um key in this in this this output
00:48:42.080 | formulation you will get if the two are perfectly orthogonal zero dot product you will get an exact
00:48:48.160 | recall of the values with no loss whatsoever now if they're if they're like mostly orthogonal you'll get
00:48:54.320 | 99 98 recall whatever that's that's good enough to the extent that you put in a query that's kind of a mix
00:49:01.920 | between different keys then you're going to get a weighted blended average of the different keys which is
00:49:08.880 | exactly what we see in softmax tension um you you're getting a blend of the different things of the
00:49:14.880 | different values that are getting a weighted sum of values based on your tension scores okay so the shape
00:49:21.760 | of this is a little different in that this one is two times d assuming that that dk equals dv the height of
00:49:29.840 | this is 2d and the height of this is only 1d so this is actually even a more efficient representation
00:49:36.560 | because we're taking advantage of this linear algebra stuff we don't actually have to store
00:49:40.960 | the the the the keys and the values in separate sections we by multiplying them together and taking
00:49:48.080 | advantage of orthogonality we just slam them all in here all right any questions before i move on to
00:49:55.600 | the rest of section 2.2 all right cool so let me share my screen it says the whiteboard's going to go
00:50:04.880 | away i don't know if it can be saved brought back whatever but one sec one sec let me uh let me save it or
00:50:13.760 | add an option to save it as a pdf or something yeah there is a way to save them yeah i got it
00:50:20.400 | i got it whiteboard i can save it as a template and i can also just export it as a p yeah just export it
00:50:27.840 | to pdf if you would be so kind yep i got one png i'll also do a pdf and then we can figure out how to
00:50:35.920 | get it all right it's not that beautiful so people all right it's still there still there okay go ahead
00:50:40.960 | and get rid of it i'll bring it back if you need it all right um
00:50:45.520 | yeah and i think i can bring it back but anyway all right so
00:50:52.400 | hopefully you see my screen so we just talked about this first equation
00:50:58.720 | okay this is the super simple uh way of storing things in an array and so s is simply a sum of rank
00:51:07.600 | one outer products of approximately orthogonal keys all right this thing will die as soon as you
00:51:16.240 | have one more thing than whatever the dimensionality is so if it's if it's you know 1024 it'll work
00:51:22.320 | great for the first 1024 things and then it's not going to work um once you try to put something else in
00:51:29.280 | so uh one of the things you can do is um you can have this this delta rule which basically says that
00:51:40.800 | i'm going to subtract a little bit out in order to make room for the new thing that i'm adding um that's
00:51:48.240 | what this business that gets you to this equation that's what this business is about i'm not going to
00:51:53.760 | go into like super super detail but ultimately um what what then people evolve to is this idea which for
00:52:05.840 | people here will probably be more familiar is this idea of weight decay so if you imagine that that
00:52:11.920 | square matrix we have that's our memory store if you just apply a little bit of weight decay every time
00:52:16.960 | you get a new token you multiply that whole matrix by 0.95 okay then what's going to happen is something
00:52:23.040 | that's very old will have been multiplied by 0.9 over and over and over and over and over again and it will
00:52:28.240 | eventually get close to zeroed out without you having to explicitly do anything okay and so that's where you
00:52:35.680 | basically have this scalar alpha that's like your weight decay in in our in our weight matrices that we use
00:52:42.640 | when we're doing you know gradient descent when we're doing like atom w right um so it every time you get
00:52:49.200 | a new token you just multiply it by this um and and the old ones uh will decay and so the idea here is that
00:52:58.160 | uh i is the identity matrix so our update after we get a new token is the identity times the old
00:53:06.080 | matrix so that's just the old matrix minus um this particular thing which is the which is the making
00:53:14.720 | room forgetting component here okay plus this is our brand new key and our brand new value so this is the
00:53:22.960 | thing that we're adding into the memory all right and then we're going to take this whole old thing
00:53:28.320 | and we're going to decay it by some you know whatever 0.95 some some you know value like this
00:53:33.840 | and this thing actually worked pretty well it was pretty stable so that if you got past a thousand
00:53:40.320 | tokens and you went to fifteen hundred two thousand three thousand it kind of mostly remembered the last
00:53:46.800 | one thousand tokens so it works a lot like sliding window attention okay so i i saw the comment early
00:53:54.240 | in the chat why not just do sliding window okay it works like that however it is a little bit smarter
00:54:00.560 | than that where you can selectively say if a concept is super important i will keep it even though it's
00:54:06.560 | more than a thousand tokens ago all right um so hypothetically if if you train a model on stories
00:54:13.840 | and the first sentence says our main character is named bob it could decide that that based on
00:54:19.760 | context it's gonna like never forget that thing and it's gonna really really make sure that bob stays
00:54:25.680 | in the in the memory because it's super important if you use a sliding window it it's it's a hard-coded
00:54:31.040 | rule it's only the last thousand tokens and so you you can't have that selectivity whether or not
00:54:36.640 | your model is smart enough to learn that rule to know that it should remember bob is a whole separate
00:54:41.440 | thing but that's why they they train these models to try to get them to work so finally um if you have
00:54:48.960 | this idea of weight decay we're decaying all of the entries in there simultaneously and equally um now
00:54:57.440 | you can say i'm going to decay them uh uh uh based on what the current token is and then the final thing that they do
00:55:06.880 | in kimmy in this in this kimmy linear kda they say this old entry is um a float of length 2048 i'm only
00:55:20.560 | going to decay of the 2048 floats only decay the ones that i really want to um and i can selectively choose
00:55:28.560 | and so instead of having up here it's a scalar a 0.95 that multiplies by all the weights i'm now
00:55:35.200 | actually going to say this skip this is now not a scalar it's a vector um and they make it a diagonal
00:55:42.000 | matrix but it's effectively just saying each component i will choose so maybe the first 10 floats 0.95 and
00:55:48.080 | the rest of the floats is one i'm not going to decay them at all so at the end of the day that's the that's
00:55:53.680 | the trick and so then they say we have this efficient algorithm for doing parallel when we have pre-fill
00:55:59.760 | or training when we have all the tokens at once it's an rnn so it's always really fast when you're
00:56:04.720 | doing one token at a time and then what we can do is we can compare it to other linear uh things that came
00:56:14.480 | before so for example you may remember uh mamba uh you may remember a gated delta net which is a little
00:56:23.040 | more recent and so this thing actually if you look at these curves mamba 2 is the orange line and on
00:56:30.080 | accuracy um it smokes it and then gated delta nets newer and it's it's similar but like a little bit
00:56:36.720 | better um in performance so then they get into uh i know we're out of time so then they get into um
00:56:44.400 | some simple experiments to show that their linear attention alone in a toy model with two layers
00:56:49.680 | outperforms older things outperforms linformer mamba mamba 2 rwkv uh uh gated delta net we we outperform all
00:56:58.880 | those on a few things that linear models tend to have difficulty on like reversing a strain
00:57:04.960 | um and doing like multiple recall um so now that we're confident that we have a better linear
00:57:11.680 | component let's actually stick it in a model and then we're going to do some ablations with um how
00:57:18.160 | much full attention do we need they come up with one quarter full attention is good if you do more than
00:57:23.520 | a quarter full attention you get almost identical performance at more cost if you do less than a
00:57:28.720 | quarter if you do like one eighth full attention they found that the performance drops so that's why they
00:57:34.320 | they don't have to worry about what they're doing but they don't have to worry about what they're going
00:57:38.240 | to do and they don't have to worry about it they don't have to worry about it they don't have to worry
00:57:41.040 | that they don't have to worry about it they don't have to worry about it they don't have to worry about
00:57:43.040 | it they don't have to worry about it and they don't have to worry about it and they don't have to worry about
00:57:43.600 | it they don't have to worry about it and they don't have to worry about it and they don't have to worry about it
00:57:45.040 | and i'm not sure if they did their ablations completely right i'm not sure how they handled rope for the the baselines
00:57:53.040 | for the the baselines but basically what they found was that if they took away positional embeddings for
00:58:00.400 | the quarter of the layers that were full attention it actually performed better than if they gave it
00:58:05.840 | positional information and what they argued is that attention is so regular attention is so good at
00:58:12.000 | positional information that it it trumps the kda and says i will take care of short-term dependencies
00:58:20.400 | when they took attention when they took a rope away from the full attention layers it was like
00:58:25.760 | well i can't do any positional information because i don't have anything and so it fully delegated all
00:58:31.680 | the responsibility for previous token two tokens ago to the kda layers that allowed the regular attention
00:58:40.560 | layers to 100 percent focus on long context semantic tasks give me the nouns give me the last time i saw
00:58:48.000 | the name bob give me all of those things and not focus any of its energy on short-term things there
00:58:55.200 | may be some other dynamics going on here but i'm particularly uh um on event that regular rope is
00:59:01.840 | kind of stupid we should be using at least truncated rope mla they separate the rope so that it's not
00:59:08.480 | actually adding noise uh to the normally rope you know you you multiply it and so you're you're noising
00:59:15.120 | your your token signal uh for mla you concatenate it so you're not noising your signal so i think there's
00:59:21.120 | some things that that will my personal opinion is we're going to learn some things about how rope is
00:59:27.840 | awesome it beats all the other positional embeddings but there is a cost to it and that we can be a little
00:59:32.400 | bit smarter about it and that's why they found that by by taking it away from the the regular attention
00:59:39.680 | layers so that for me was like the most um interesting thing uh um the rest of it is like hey we ran some
00:59:47.120 | experiments and did really well they make these strong claims that they outperformed a model with
00:59:54.320 | the same training recipe same number of tokens but just all full attention layers instead of a quarter full and
01:00:01.520 | three quarters kda i would believe it but i i think it's possible that that they may have messed up
01:00:10.080 | their relations but if they do in fact beat it i think my personal take is it's not because the kda is so
01:00:18.320 | awesome it's because rope has a cost and they actually managed to find a way to measure that cost
01:00:26.080 | and by removing rope from the from the full attention layers they actually let the attention do what it does
01:00:32.080 | really well without any noise but that's just ted's hot take all right i can i can stay longer if if
01:00:40.720 | people have questions or want to talk about it but with respect for the people who may need to go i think
01:00:45.440 | that's the most important thing to know about it so there are other models out there that are doing the
01:00:49.520 | hybrid i saw some stuff in the chat so so yeah like three quarters something faster one quarter full attention
01:00:56.960 | means you get three quarters smaller uh kv cache much much faster decoding because decoding is memory
01:01:03.440 | bound and as long as it doesn't totally kill you on on in context learning then then it's like sort of an
01:01:12.240 | overall win
01:01:15.040 | thank you um i understand a lot more about kda um after your step-by-step walkthrough just wanted to say that
01:01:29.040 | thanks
01:01:30.640 | any questions
01:01:35.520 | all right so i don't know if that's a good sign that it was clear or i just completely lost
01:01:44.320 | everybody so if you go back to this diagram they didn't label it but on the left this is the queries
01:01:49.680 | in the keys and so like usual you take your your your um your your token you run it through a weight
01:01:57.440 | matrix w sub q w sub k uh if you remember mamba they have some uh 1d convolutions that they run it through
01:02:04.880 | um and those are helpful and like you know 1d convolution can very easily just find simple patterns
01:02:10.320 | um this is a normal there's normalization layers everywhere this is a normalization layer uh qk norm like
01:02:17.600 | quen has this is the values totally uh again normal except they run it through convolution
01:02:23.600 | one trick they do is on their alpha um they use something akin to uh laura where they take two
01:02:32.560 | rectangular low rank matrices and multiply them together to make a square matrix uh just because
01:02:37.680 | they don't really need that whatever the heck it is d squared numbers of parameters um and they do a
01:02:44.800 | similar trick uh on the on the final output gate and then this is um there uh uh beta the the forget
01:02:54.160 | factor so everything on here is channel uh um aware so there's nothing here that applies equally to all 2048
01:03:04.320 | floats anything they do whether they're adding subtracting multiplying it's always going to be at least
01:03:11.120 | dimensionality d um and this is the uh this is the gate that you see in gated attention uh i don't know
01:03:21.200 | i don't remember which other models have gated attention now uh uh uh the latest quen have it um but
01:03:27.840 | anyway so normally what you do is you calculate all your attention you just add that to the residual stream
01:03:33.600 | okay so this sucker has a sigmoid on it that says hey if you're layer three and for some reason you're
01:03:40.080 | sort of less important i'm going to actually multiply your output by 0.5 and so you're going to have a
01:03:45.760 | quieter addition to the residual stream and if you're a super important layer then you're going to get the full
01:03:51.600 | level 1.0 um and if you guys know about like um attention seeks attention sinks and massive
01:04:01.520 | activations um that's one of the things that researchers seem to be trying to fight and so
01:04:09.200 | they think that if they add some of these normalizations in they don't get as large spiking activations
01:04:15.680 | which i think helps them when they're trying to go to smaller and smaller quantization
01:04:20.560 | because now they don't have such extreme values that they need to support and so i think the holy
01:04:25.520 | grail is you figure out some kind of normalizations and gatings such that all your activations stay in a
01:04:33.120 | nice little gaussian distribution and then you can totally nail it with something like you know fp4 in
01:04:40.560 | four or whatever but right now if you have these activations and then occasionally you have an
01:04:45.040 | activation that's a hundred times larger it's just it's just very difficult in low precision to support
01:04:51.600 | an activation so that's why in these things you still see right like the the weights are small but
01:04:56.720 | the activations are still 16-bit it's because you have these hundred thousand times larger activations
01:05:02.400 | if you if you if you really quash those you go down to eight bit activations and maybe eventually
01:05:08.480 | four bit activations so that's like a little more detail if you actually go through sort of like
01:05:16.000 | this is what the the layers look like and you see there's just a few extra normalizations in here
01:05:20.480 | and i had a question about you had mentioned at the beginning you drew a parallel between linear
01:05:33.360 | and colonel methods and kernel methods and i i have i think i understand kernel kernel methods reasonably
01:05:40.400 | well i just wanted to understand your parallel you're drawing there um i i don't know if i can do a great
01:05:47.040 | job explaining it so i gave the the associative memory analogy for how to understand this
01:05:54.480 | okay um the other way of thinking about it is that um if you if you have this n by n uh uh attention
01:06:07.360 | pattern well it may be lower triangular because of of of of of of of of of of of causal attention or whatever
01:06:14.720 | but still if you just think about it the pattern can look like anything okay and the high values
01:06:20.880 | and the low values are not necessarily linearly separable um and because so if the high values
01:06:29.280 | and the low values look like some sort of xor pattern where it's like high low high then if instead of
01:06:36.000 | using a full n squared thing and a soft max if you try to squash this to just a one-dimensional
01:06:44.240 | representation a linear representation you can only do linearly separable in a way that the highs have
01:06:52.080 | to all be on one side and lows have to be on the other side and that is the the somewhat mathematical
01:06:58.480 | uh uh uh interpretation for why linear attention you know whatever lin form or per form or mamba one
01:07:06.480 | cannot be as expressive why they hit a glass ceiling that soft max full attention doesn't hit when you
01:07:12.880 | start training these really large models um so if you imagine that you then take those those attention
01:07:22.080 | patterns and you run them through some other function so the classic one uh uh if you want
01:07:28.960 | i can pull it up real quick is but so you you have sort of like high low values uh centered on zero and
01:07:35.680 | then if you do x squared and you turn it into a parabola okay then the high values are all up here and
01:07:41.920 | the low values are all down here in in the in the bottom of the parabola and now they're linearly separable
01:07:48.480 | right in the higher dimension okay so that's that's one of the interpretations for these linear uh
01:07:56.640 | attentions is that they do some sort of transform to get them into a different dimension in which they
01:08:03.920 | are linearly separable uh and if you could do that perfectly theoretically you you would get the same
01:08:13.120 | performance as as full n squared softmax attention um i i i don't know the math well enough to know if the
01:08:22.880 | problem is that you can't do that or i think the problem might just be that we're not learning super
01:08:31.200 | complex transforms they're just using these like very fast to compute transforms and therefore that fast to
01:08:39.520 | compute thing might not cover every possible scenario and in some scenarios uh even though it gets to
01:08:45.600 | learn the queries and the keys to you know fit its purposes it's still not finding something that's
01:08:51.280 | linearly separable uh probably just because there's so many millions of different concepts and you have
01:08:55.920 | so many heads and at the end of the day it wants to do something and it can't it can't make everything it
01:09:01.440 | wants to do linearly separable right it's a glass ceiling and the non-linearity that it's using
01:09:07.520 | is basically a polynomial one through the recurrence relation is that the idea uh the math is getting
01:09:15.440 | beyond me pretty quickly the original like rnns uh uh uh uh uh uh transformers are rnns paper that's like
01:09:24.240 | four years old i think whatever yeah if you look at that i think that's the best reference for you'll see
01:09:29.440 | they have this fee function that's there so like like support vector machines what you what they do
01:09:36.400 | is they say we're going to have this kernel that transforms it but we want something that's super
01:09:41.360 | fast to compute and so the kernel trick allows you to compute these dot products super fast for svms
01:09:47.920 | without actually explicitly doing the transform so they they make a similar argument there where it's like
01:09:54.640 | yes there may be all sorts of different transforms you could use we're just going to pick this one
01:09:59.360 | because it's fast and i think ultimately that's where you get bottlenecked because you're gonna lose some
01:10:06.000 | expressivity and also you're not training that function bespoke for whatever the the the the lm's trying to do so
01:10:18.800 | if somehow you had a way of like picking the function per head per layer then maybe you could
01:10:26.320 | actually get these these linear models to perform even better but the good news is that since that paper
01:10:32.240 | since mamba one mamba two rwkb it looks like the kimmy people are saying that their linear attention
01:10:40.400 | which has slightly different update rules and slightly different forget rules outperforms all
01:10:45.840 | prior linear attention uh it's still not good enough you notice they didn't build it 100 kda
01:10:52.960 | they still say one quarter regular attention but it's still better than if you did three quarters
01:10:58.320 | mamba layers better than if you did three quarters gated delta net layers yeah okay got it i'm gonna
01:11:05.280 | i'm gonna check out that paper you said it was transformers are rns yeah yeah okay yep something
01:11:12.640 | like that let me see if i can find the exact thing
01:11:37.600 | yeah i think i found it it was uh let's see icml20
01:11:43.920 | okay yeah and there's multiple so i'm getting them confused i just found one that's the
01:11:50.720 | fast autoregressive transformers with linear attention
01:11:54.480 | oh is that's what i found too yeah yeah yeah so maybe that is the one that i was thinking of um
01:12:01.280 | let me just take a quick peek at the paper
01:12:04.640 | yep that's the one you see these these fee functions that they talk about for these transforms
01:12:11.520 | yep so you can see they they wrap a a function fee around around all of their query and their key
01:12:19.120 | type things yeah yeah
01:12:22.800 | all right awesome thank you the silence is scaring me i think i think i lost people but
01:12:32.560 | hopefully hopefully this gives you a little better insight into kda
01:12:41.360 | thanks ted yeah this is amazing thank you really appreciate it really thanks do you like i have a
01:12:48.960 | i have a question actually um this is my last this is like the question um i was wondering um if
01:12:55.920 | this means that inference for linear intention might be well better um like it does this mean that we're
01:13:07.280 | going to move to distillation for linear models and then training for full attention during full attention
01:13:17.120 | i was just reading some papers on that and it seemed to make sense given what you're saying like
01:13:22.720 | i i don't know if that if if what i'm saying makes sense but yeah yeah so the kimmy people are saying
01:13:30.480 | this can be a full drop-in replacement so it will train faster it will pre-fill faster uh i don't know
01:13:38.880 | if it's pre-fill faster but it'll decode faster um than regular full attention so you can just completely
01:13:48.160 | according to the paper's claims scrap your regular attention models and and replace it with one quarter
01:13:55.040 | retention models with kda i think that claim is a bit strong and and you know proof time may tell but
01:14:03.600 | but yes so you don't necessarily need to do anything fancy in terms of distillation or there's that you
01:14:07.680 | can just train this instead of a regular full attention models what they're claiming
01:14:10.880 | all right i just realized that my chat was not auto scrolling and so i thought there were no
01:14:19.040 | messages there's like 80 bazillion messages i don't read all right on the other side um if anyone wants
01:14:34.800 | to volunteer for next weeks i think we have a few that were posted in discord otherwise you know we'll
01:14:40.640 | continue continue discussion and everything down there in discord next week aie new york if any of you guys are
01:14:48.160 | in new york come to come to conference and you know we'll do something latent space in person where's
01:14:54.320 | the discord uh you can find it on the luma or yeah it's a search latent space discord and there's a
01:15:00.400 | paper club channel you'll find it in there cool cool awesome yeah luma slash ls and then you can you can
01:15:09.440 | find it latent spaces all right thanks ted um and same uh ai engineer new york stuff there's a channel in
01:15:18.000 | and disport people talking about it cool take care guys