Hi everyone. Today we are continuing our implementation of MakeMore, our favorite character-level language model. Now, you'll notice that the background behind me is different. That's because I am in Kyoto and it is awesome. So I'm in a hotel room here. Now, over the last few lectures we've built up to this architecture that is a multi-layer perceptron character-level language model.

So we see that it receives three previous characters and tries to predict the fourth character in a sequence using a very simple multi-layer perceptron using one hidden layer of neurons with tenational neurities. So what I'd like to do now in this lecture is I'd like to complexify this architecture.

In particular, we would like to take more characters in a sequence as an input, not just three. And in addition to that, we don't just want to feed them all into a single hidden layer because that squashes too much information too quickly. Instead, we would like to make a deeper model that progressively fuses this information to make its guess about the next character in a sequence.

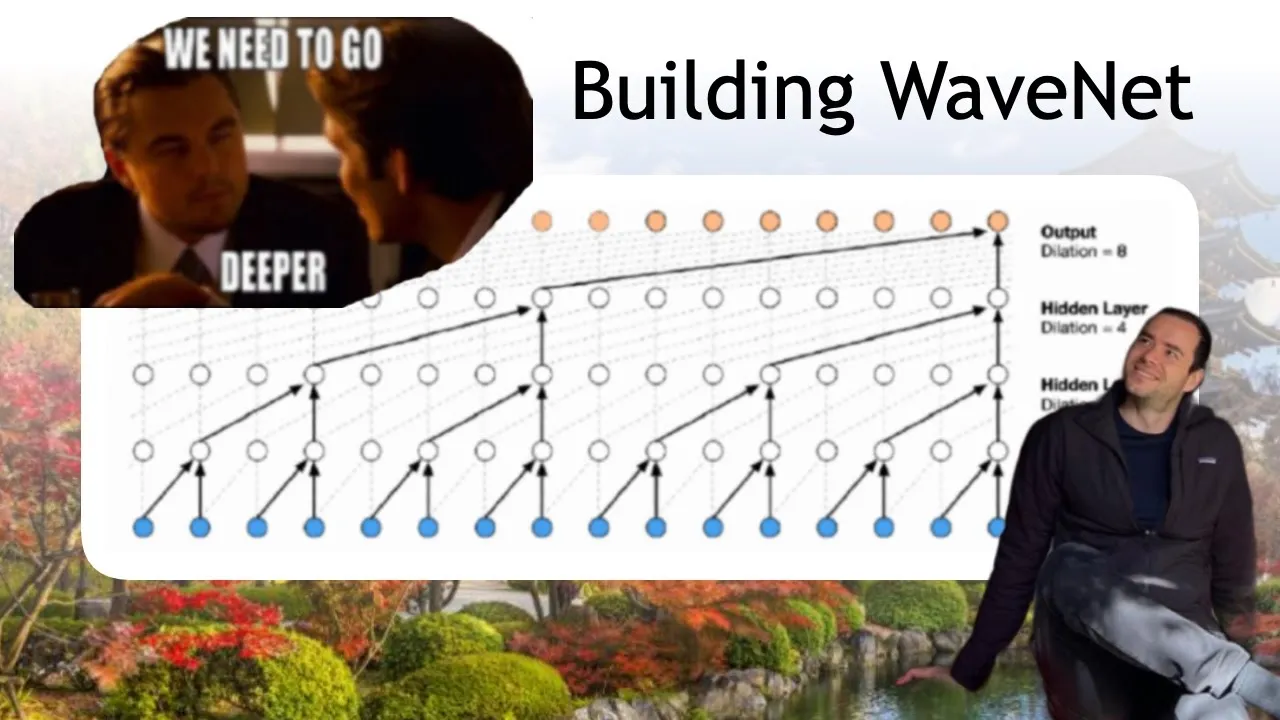
And so we'll see that as we make this architecture more complex, we're actually going to arrive at something that looks very much like a WaveNet. So WaveNet is this paper published by DeKind in 2016, and it is also a language model basically, but it tries to predict audio sequences instead of character-level sequences or word-level sequences.

But fundamentally, the modeling setup is identical. It is an autoregressive model and it tries to predict the next character in a sequence. And the architecture actually takes this interesting hierarchical sort of approach to predicting the next character in a sequence with this tree-like structure. And this is the architecture, and we're going to implement it in the course of this video.

So let's get started. So the story code for part five is very similar to where we ended up in part three. Recall that part four was the manual backpropagation exercise that is kind of an aside. So we are coming back to part three, copy-pasting chunks out of it, and that is our starter code for part five.

I've changed very few things otherwise. So a lot of this should look familiar to you if you've gone through part three. So in particular, very briefly, we are doing imports. We are reading our data set of words, and we are processing the data set of words into individual examples, and none of this data generation code has changed.

And basically, we have lots and lots of examples. In particular, we have 182,000 examples of three characters trying to predict the fourth one. And we've broken up every one of these words into little problems of given three characters, predict the fourth one. So this is our data set, and this is what we're trying to get the neural net to do.

Now, in part three, we started to develop our code around these layer modules that are, for example, a class linear. And we're doing this because we want to think of these modules as building blocks and like a Lego building block bricks that we can sort of like stack up into neural networks.

And we can feed data between these layers and stack them up into sort of graphs. Now, we also developed these layers to have APIs and signatures very similar to those that are found in PyTorch. So we have torch.nn, and it's got all these layer building blocks that you would use in practice.

And we were developing all of these to mimic the APIs of these. So for example, we have linear. So there will also be a torch.nn.linear, and its signature will be very similar to our signature, and the functionality will be also quite identical as far as I'm aware. So we have the linear layer with the batch norm 1D layer and the 10H layer that we developed previously.

And linear just does a matrix multiply in the forward pass of this module. Batch norm, of course, is this crazy layer that we developed in the previous lecture. And what's crazy about it is, well, there's many things. Number one, it has these running mean and variances that are trained outside of back propagation.

They are trained using exponential moving average inside this layer, what we call the forward pass. In addition to that, there's this training flag because the behavior of batch norm is different during train time and evaluation time. And so suddenly, we have to be very careful that batch norm is in its correct state, that it's in the evaluation state or training state.

So that's something to now keep track of, something that sometimes introduces bugs because you forget to put it into the right mode. And finally, we saw that batch norm couples the statistics or the activations across the examples in the batch. So normally, we thought of the batch as just an efficiency thing.

But now, we are coupling the computation across batch elements, and it's done for the purposes of controlling the activation statistics as we saw in the previous video. So it's a very weird layer, at least a lot of bugs, partly, for example, because you have to modulate the training and eval phase and so on.

In addition, for example, you have to wait for the mean and the variance to settle and to actually reach a steady state. And so you have to make sure that you... Basically, there's state in this layer, and state is harmful, usually. Now, I brought out the generator object. Previously, we had a generator equals G and so on inside these layers.

I've discarded that in favor of just initializing the torch RNG outside here just once globally, just for simplicity. And then here, we are starting to build out some of the neural network elements. This should look very familiar. We have our embedding table C, and then we have a list of layers.

And it's a linear, feeds to batch or feeds to 10H, and then a linear output layer. And its weights are scaled down, so we are not confidently wrong at initialization. We see that this is about 12,000 parameters. We're telling PyTorch that the parameters require gradients. The optimization is, as far as I'm aware, identical and should look very, very familiar.

Nothing changed here. Lost function looks very crazy. We should probably fix this. And that's because 32 batch elements are too few. And so you can get very lucky or unlucky in any one of these batches, and it creates a very thick loss function. So we're going to fix that soon.

Now, once we want to evaluate the trained neural network, we need to remember, because of the batch norm layers, to set all the layers to be training equals false. This only matters for the batch norm layer so far. And then we evaluate. We see that currently we have a validation loss of 2.10, which is fairly good, but there's still a ways to go.

But even at 2.10, we see that when we sample from the model, we actually get relatively name-like results that do not exist in a training set. So for example, Yvonne, Kilo, Pras, Alaya, et cetera. So certainly not unreasonable, I would say, but not amazing. And we can still push this validation loss even lower and get much better samples that are even more name-like.

So let's improve this model now. OK, first, let's fix this graph, because it is daggers in my eyes, and I just can't take it anymore. So loss_i, if you recall, is a Python list of floats. So for example, the first 10 elements look like this. Now, what we'd like to do basically is we need to average up some of these values to get a more representative value along the way.

So one way to do this is the following. In PyTorch, if I create, for example, a tensor of the first 10 numbers, then this is currently a one-dimensional array. But recall that I can view this array as two-dimensional. So for example, I can view it as a 2x5 array, and this is a 2D tensor now, 2x5.

And you see what PyTorch has done is that the first row of this tensor is the first five elements, and the second row is the second five elements. I can also view it as a 5x2, as an example. And then recall that I can also use -1 in place of one of these numbers, and PyTorch will calculate what that number must be in order to make the number of elements work out.

So this can be this, or like that. Both will work. Of course, this would not work. Okay, so this allows it to spread out some of the consecutive values into rows. So that's very helpful, because what we can do now is, first of all, we're going to create a Torch.tensor out of the list of floats.

And then we're going to view it as whatever it is, but we're going to stretch it out into rows of 1,000 consecutive elements. So the shape of this now becomes 200 by 1,000, and each row is 1,000 consecutive elements in this list. So that's very helpful, because now we can do a mean along the rows, and the shape of this will just be 200.

And so we've taken basically the mean on every row. So plt.plot of that should be something nicer. Much better. So we see that we've basically made a lot of progress. And then here, this is the learning rate decay. So here we see that the learning rate decay subtracted a ton of energy out of the system, and allowed us to settle into the local minimum in this optimization.

So this is a much nicer plot. Let me come up and delete the monster, and we're going to be using this going forward. Now, next up, what I'm bothered by is that you see our forward pass is a little bit gnarly, and takes way too many lines of code.

So in particular, we see that we've organized some of the layers inside the layers list, but not all of them for no reason. So in particular, we see that we still have the embedding table special case outside of the layers. And in addition to that, the viewing operation here is also outside of our layers.

So let's create layers for these, and then we can add those layers to just our list. So in particular, the two things that we need is here, we have this embedding table, and we are indexing at the integers inside the batch xb, inside the tensor xb. So that's an embedding table lookup just done with indexing.

And then here we see that we have this view operation, which if you recall from the previous video, simply rearranges the character embeddings and stretches them out into a row. And effectively, what that does is the concatenation operation, basically, except it's free because viewing is very cheap in PyTorch.

And no memory is being copied. We're just re-representing how we view that tensor. So let's create modules for both of these operations, the embedding operation and the flattening operation. So I actually wrote the code just to save some time. So we have a module embedding and a module flatten, and both of them simply do the indexing operation in a forward pass and the flattening operation here.

And this c now will just become a self.weight inside an embedding module. And I'm calling these layers specifically embedding and flatten because it turns out that both of them actually exist in PyTorch. So in PyTorch, we have n and dot embedding, and it also takes the number of embeddings and the dimensionality of the embedding, just like we have here.

But in addition, PyTorch takes in a lot of other keyword arguments that we are not using for our purposes yet. And for flatten, that also exists in PyTorch, and it also takes additional keyword arguments that we are not using. So we have a very simple flatten. But both of them exist in PyTorch, they're just a bit more simpler.

And now that we have these, we can simply take out some of these special cased things. So instead of c, we're just going to have an embedding and a vocab size and n embed. And then after the embedding, we are going to flatten. So let's construct those modules. And now I can take out this c.

And here, I don't have to special case it anymore, because now c is the embedding's weight, and it's inside layers. So this should just work. And then here, our forward pass simplifies substantially, because we don't need to do these now outside of these layer, outside and explicitly. They're now inside layers, so we can delete those.

But now to kick things off, we want this little x, which in the beginning is just xb, the tensor of integers specifying the identities of these characters at the input. And so these characters can now directly feed into the first layer, and this should just work. So let me come here and insert a break, because I just want to make sure that the first iteration of this runs and that there's no mistake.

So that ran properly. And basically, we've substantially simplified the forward pass here. Okay, I'm sorry, I changed my microphone. So hopefully, the audio is a little bit better. Now, one more thing that I would like to do in order to PyTorchify our code in further is that right now, we are maintaining all of our modules in a naked list of layers.

And we can also simplify this, because we can introduce the concept of PyTorch containers. So in torch.nn, which we are basically rebuilding from scratch here, there's a concept of containers. And these containers are basically a way of organizing layers into lists or dicts and so on. So in particular, there's a sequential, which maintains a list of layers, and is a module class in PyTorch.

And it basically just passes a given input through all the layers sequentially, exactly as we are doing here. So let's write our own sequential. I've written a code here. And basically, the code for sequential is quite straightforward. We pass in a list of layers, which we keep here. And then given any input in a forward pass, we just call the layers sequentially and return the result.

And in terms of the parameters, it's just all the parameters of the child modules. So we can run this. And we can again simplify this substantially. Because we don't maintain this naked list of layers. We now have a notion of a model, which is a module. And in particular, is a sequential of all these layers.

And now, parameters are simply just model.parameters. And so that list comprehension now lives here. And then here we are doing all the things we used to do. Now here, the code again simplifies substantially. Because we don't have to do this forwarding here. Instead, we just call the model on the input data.

And the input data here are the integers inside xb. So we can simply do logits, which are the outputs of our model, are simply the model called on xb. And then the cross entropy here takes the logits and the targets. So this simplifies substantially. And then this looks good.

So let's just make sure this runs. That looks good. Now here, we actually have some work to do still here, but I'm going to come back later. For now, there's no more layers. There's a model that layers, but it's not easy to access attributes of these classes directly. So we'll come back and fix this later.

And then here, of course, this simplifies substantially as well, because logits are the model called on x. And then these logits come here. So we can evaluate the train and validation loss, which currently is terrible because we just initialized the neural net. And then we can also sample from the model.

And this simplifies dramatically as well, because we just want to call the model onto the context and outcome logits. And then these logits go into Softmax and get the probabilities, etc. So we can sample from this model. What did I screw up? Okay, so I fixed the issue and we now get the result that we expect, which is gibberish because the model is not trained because we reinitialize it from scratch.

The problem was that when I fixed this cell to be modeled out layers instead of just layers, I did not actually run the cell. And so our neural net was in a training mode. And what caused the issue here is the batch norm layer, as batch norm layer often likes to do, because batch norm was in the training mode.

And here we are passing in an input, which is a batch of just a single example made up of the context. And so if you are trying to pass in a single example into a batch norm that is in the training mode, you're going to end up estimating the variance using the input.

And the variance of a single number is not a number, because it is a measure of a spread. So for example, the variance of just a single number five, you can see is not a number. And so that's what happened. And batch norm basically caused an issue. And then that polluted all of the further processing.

So all that we had to do was make sure that this runs. And we basically made the issue of, again, we didn't actually see the issue with the loss. We could have evaluated the loss, but we got the wrong result because batch norm was in the training mode. And so we still get a result, it's just the wrong result, because it's using the sample statistics of the batch.

Whereas we want to use the running mean and running variance inside the batch norm. And so again, an example of introducing a bug inline, because we did not properly maintain the state of what is training or not. Okay, so I re-run everything. And here's where we are. As a reminder, we have the training loss of 2.05 and validation 2.10.

Now, because these losses are very similar to each other, we have a sense that we are not overfitting too much on this task. And we can make additional progress in our performance by scaling up the size of the neural network and making everything bigger and deeper. Now, currently, we are using this architecture here, where we are taking in some number of characters, going into a single hidden layer, and then going to the prediction of the next character.

The problem here is, we don't have a naive way of making this bigger in a productive way. We could, of course, use our layers, sort of building blocks and materials to introduce additional layers here and make the network deeper. But it is still the case that we are crushing all of the characters into a single layer all the way at the beginning.

And even if we make this a bigger layer and add neurons, it's still kind of like silly to squash all that information so fast in a single step. So we'd like to do instead is we'd like our network to look a lot more like this in the WaveNet case.

So you see in the WaveNet, when we are trying to make the prediction for the next character in the sequence, it is a function of the previous characters that feed in. But not all of these different characters are not just crushed to a single layer, and then you have a sandwich.

They are crushed slowly. So in particular, we take two characters and we fuse them into sort of like a bigram representation. And we do that for all these characters consecutively. And then we take the bigrams and we fuse those into four character level chunks. And then we fuse that again.

And so we do that in this like tree-like hierarchical manner. So we fuse the information from the previous context slowly into the network as it gets deeper. And so this is the kind of architecture that we want to implement. Now, in the WaveNet's case, this is a visualization of a stack of dilated causal convolution layers.

And this makes it sound very scary, but actually the idea is very simple. And the fact that it's a dilated causal convolution layer is really just an implementation detail to make everything fast. We're going to see that later. But for now, let's just keep the basic idea of it, which is this progressive fusion.

So we want to make the network deeper. And at each level, we want to fuse only two consecutive elements, two characters, then two bigrams, then two fourgrams, and so on. So let's implement this. Okay, so first up, let me scroll to where we built the dataset. And let's change the block size from three to eight.

So we're going to be taking eight characters of context to predict the ninth character. So the dataset now looks like this. We have a lot more context feeding in to predict any next character in a sequence. And these eight characters are going to be processed in this tree-like structure.

Now, if we scroll here, everything here should just be able to work. So we should be able to redefine the network. You see that the number of parameters has increased by 10,000. And that's because the block size has grown. So this first linear layer is much, much bigger. Our linear layer now takes eight characters into this middle layer.

So there's a lot more parameters there. But this should just run. Let me just break right after the very first iteration. So you see that this runs just fine. It's just that this network doesn't make too much sense. We're crushing way too much information way too fast. So let's now come in and see how we could try to implement the hierarchical scheme.

Now, before we dive into the detail of the reimplementation here, I was just curious to actually run it and see where we are in terms of the baseline performance of just lazily scaling up the context length. So I let it run. We get a nice loss curve. And then evaluating the loss, we actually see quite a bit of improvement just from increasing the context length.

So I started a little bit of a performance log here. And previously where we were is we were getting a performance of 2.10 on the validation loss. And now simply scaling up the context length from three to eight gives us a performance of 2.02. So quite a bit of an improvement here.

And also, when you sample from the model, you see that the names are definitely improving qualitatively as well. So we could, of course, spend a lot of time here tuning things and making it even bigger and scaling up the network further, even with a simple set up here. But let's continue.

And let's implement the hierarchical model and treat this as just a rough baseline performance. But there's a lot of optimization left on the table in terms of some of the hyperparameters that you're hopefully getting a sense of now. OK, so let's scroll up now and come back up. And what I've done here is I've created a bit of a scratch space for us to just look at the forward pass of the neural net and inspect the shape of the tensors along the way as the neural net forwards.

So here I'm just temporarily for debugging, creating a batch of just, say, four examples, so four random integers. Then I'm plucking out those rows from our training set. And then I'm passing into the model the input xb. Now, the shape of xb here, because we have only four examples, is four by eight.

And this eight is now the current block size. So inspecting xb, we just see that we have four examples. Each one of them is a row of xb. And we have eight characters here. And this integer tensor just contains the identities of those characters. So the first layer of our neural net is the embedding layer.

So passing xb, this integer tensor, through the embedding layer creates an output that is four by eight by 10. So our embedding table has, for each character, a 10-dimensional vector that we are trying to learn. And so what the embedding layer does here is it plucks out the embedding vector for each one of these integers and organizes it all in a four by eight by 10 tensor now.

So all of these integers are translated into 10-dimensional vectors inside this three-dimensional tensor now. Now, passing that through the flattened layer, as you recall, what this does is it views this tensor as just a four by 80 tensor. And what that effectively does is that all these 10-dimensional embeddings for all these eight characters just end up being stretched out into a long row.

And that looks kind of like a concatenation operation, basically. So by viewing the tensor differently, we now have a four by 80. And inside this 80, it's all the 10-dimensional vectors just concatenated next to each other. And the linear layer, of course, takes 80 and creates 200 channels just via matrix multiplication.

So, so far, so good. Now I'd like to show you something surprising. Let's look at the insides of the linear layer and remind ourselves how it works. The linear layer here in a forward pass takes the input x, multiplies it with a weight, and then optionally adds a bias.

And the weight here is two-dimensional, as defined here, and the bias is one-dimensional here. So effectively, in terms of the shapes involved, what's happening inside this linear layer looks like this right now. And I'm using random numbers here, but I'm just illustrating the shapes and what happens. Basically, a four by 80 input comes into the linear layer, gets multiplied by this 80 by 200 weight matrix inside, and there's a plus 200 bias.

And the shape of the whole thing that comes out of the linear layer is four by 200, as we see here. Now, notice here, by the way, that this here will create a four by 200 tensor, and then plus 200, there's a broadcasting happening here. But four by 200 broadcasts with 200, so everything works here.

So now the surprising thing that I'd like to show you that you may not expect is that this input here that is being multiplied doesn't actually have to be two- dimensional. This matrix multiply operator in PyTorch is quite powerful, and in fact, you can actually pass in higher-dimensional arrays or tensors, and everything works fine.

So for example, this could be four by five by 80, and the result in that case will become four by five by 200. You can add as many dimensions as you like on the left here. And so effectively, what's happening is that the matrix multiplication only works on the last dimension, and the dimensions before it in the input tensor are left unchanged.

So basically, these dimensions on the left are all treated as just a batch dimension. So we can have multiple batch dimensions, and then in parallel over all those dimensions, we are doing the matrix multiplication on the last dimension. So this is quite convenient, because we can use that in our network now.

Because remember that we have these eight characters coming in, and we don't want to now flatten all of it out into a large eight-dimensional vector, because we don't want to matrix multiply 80 into a weight matrix multiply immediately. Instead, we want to group these like this. So every consecutive two elements, one, two, and three, and four, and five, and six, and seven, and eight, all of these should be now basically flattened out and multiplied by a weight matrix.

But all of these four groups here, we'd like to process in parallel. So it's kind of like a batch dimension that we can introduce. And then we can in parallel basically process all of these bigram groups in the four batch dimensions of an individual example, and also over the actual batch dimension of the, you know, four examples in our example here.

So let's see how that works. Effectively, what we want is right now, we take a 4 by 80, and multiply it by 80 by 200 in the linear layer. This is what happens. But instead, what we want is, we don't want 80 characters or 80 numbers to come in.

We only want two characters to come in on the very first layer, and those two characters should be fused. So in other words, we just want 20 to come in, right? 20 numbers would come in. And here, we don't want a 4 by 80 to feed into the linear layer.

We actually want these groups of two to feed in. So instead of 4 by 80, we want this to be a 4 by 4 by 20. So these are the four groups of two, and each one of them is 10-dimensional vector. So what we want is now, is we need to change the flattened layer.

So it doesn't output a 4 by 80, but it outputs a 4 by 4 by 20, where basically, every two consecutive characters are packed in on the very last dimension. And then these four is the first batch dimension, and this four is the second batch dimension, referring to the four groups inside every one of these examples.

And then this will just multiply like this. So this is what we want to get to. So we're going to have to change the linear layer in terms of how many inputs it expects. It shouldn't expect 80, it should just expect 20 numbers. And we have to change our flattened layer so it doesn't just fully flatten out this entire example.

It needs to create a 4 by 4 by 20 instead of a 4 by 80. So let's see how this could be implemented. Basically, right now, we have an input that is a 4 by 8 by 10 that feeds into the flattened layer. And currently, the flattened layer just stretches it out.

So if you remember the implementation of flatten, it takes our x, and it just views it as whatever the batch dimension is, and then negative 1. So effectively, what it does right now is it does E.view of 4, negative 1, and the shape of this, of course, is 4 by 80.

So that's what currently happens. And we instead want this to be a 4 by 4 by 20, where these consecutive 10-dimensional vectors get concatenated. So you know how in Python, you can take a list of range of 10. So we have numbers from 0 to 9. And we can index like this to get all the even parts.

And we can also index like starting at 1, and going in steps of 2 to get all the odd parts. So one way to implement this would be as follows. We can take E, and we can index into it for all the batch elements, and then just even elements in this dimension.

So at indexes 0, 2, 4, and 8. And then all the parts here from this last dimension. And this gives us the even characters. And then here, this gives us all the odd characters. And basically, what we want to do is we want to make sure that these get concatenated in PyTorch.

And then we want to concatenate these two tensors along the second dimension. So this and the shape of it would be 4 by 4 by 20. This is definitely the result we want. We are explicitly grabbing the even parts and the odd parts. And we're arranging those 4 by 4 by 10 right next to each other and concatenate.

So this works. But it turns out that what also works is you can simply use view again and just request the right shape. And it just so happens that in this case, those vectors will again end up being arranged exactly the way we want. So in particular, if we take E, and we just view it as a 4 by 4 by 20, which is what we want, we can check that this is exactly equal to, let me call this, this is the explicit concatenation, I suppose.

So explicit dot shape is 4 by 4 by 20. If you just view it as 4 by 4 by 20, you can check that when you compare to explicit, you get a bit, this is element-wise operation. So making sure that all of them are true, the values to true.

So basically, long story short, we don't need to make an explicit call to concatenate, etc. We can simply take this input tensor to flatten, and we can just view it in whatever way we want. And in particular, we don't want to stretch things out with negative one, we want to actually create a three-dimensional array.

And depending on how many vectors that are consecutive, we want to fuse, like for example, two, then we can just simply ask for this dimension to be 20. And using negative one here, and PyTorch will figure out how many groups it needs to pack into this additional batch dimension.

So let's now go into flatten and implement this. Okay, so I scrolled up here to flatten. And what we'd like to do is we'd like to change it now. So let me create a constructor and take the number of elements that are consecutive that we would like to concatenate now in the last dimension of the output.

So here, we're just going to remember, cell.n equals n. And then I want to be careful here, because PyTorch actually has a Torch.flatten, and its keyword arguments are different, and they kind of like function differently. So our flatten is going to start to depart from PyTorch.flatten. So let me call it flatten consecutive, or something like that, just to make sure that our APIs are about equal.

So this basically flattens only some n consecutive elements and puts them into the last dimension. Now here, the shape of x is b by t by c. So let me pop those out into variables and recall that in our example down below, b was 4, t was 8, and c was 10.

Now, instead of doing x.view of b by negative one, right, this is what we had before. We want this to be b by negative one by, and basically here, we want c times n. That's how many consecutive elements we want. And here, instead of negative one, I don't super love the use of negative one, because I like to be very explicit so that you get error messages when things don't go according to your expectation.

So what do we expect here? We expect this to become t divide n, using integer division here. So that's what I expect to happen. And then one more thing I want to do here is, remember previously, all the way in the beginning, n was 3, and basically we're concatenating all the three characters that existed there.

So we basically concatenated everything. And so sometimes that can create a spurious dimension of one here. So if it is the case that x.shape at one is one, then it's kind of like a spurious dimension. So we don't want to return a three-dimensional tensor with a one here. We just want to return a two-dimensional tensor exactly as we did before.

So in this case, basically, we will just say x equals x.squeeze, that is a PyTorch function. And squeeze takes a dimension that it identifies as a three-dimensional dimension, that it either squeezes out all the dimensions of a tensor that are one, or you can specify the exact dimension that you want to be squeezed.

And again, I like to be as explicit as possible always. So I expect to squeeze out the first dimension only of this tensor, this three-dimensional tensor. And if this dimension here is one, then I just want to return b by n. And so self.out will be x, and then we return self.out.

So that's the candidate implementation. And of course, this should be self.in instead of just n. So let's run. And let's come here now and take it for a spin. So flatten consecutive. And in the beginning, let's just use eight. So this should recover the previous behavior. So flatten consecutive of eight, which is the current block size.

We can do this. That should recover the previous behavior. So we should be able to run the model. And here we can inspect. I have a little code snippet here where I iterate over all the layers. I print the name of this class and the shape. And so we see the shapes as we expect them after every single layer in its output.

So now let's try to restructure it using our flatten consecutive and do it hierarchically. So in particular, we want to flatten consecutive not block size, but just two. And then we want to process this with linear. Now the number of inputs to this linear will not be n embed times block size.

It will now only be n embed times two, 20. This goes through the first layer. And now we can, in principle, just copy paste this. Now the next linear layer should expect n hidden times two. And the last piece of it should expect n hidden times two again. So this is sort of like the naive version of it.

So running this, we now have a much, much bigger model. And we should be able to basically just forward the model. And now we can inspect the numbers in between. So 4 by 8 by 20 was flattened consecutively into 4 by 4 by 20. This was projected into 4 by 4 by 200.

And then Bashorm just worked out of the box. And we have to verify that Bashorm does the correct thing, even though it takes a three-dimensional embed instead of two-dimensional embed. Then we have 10h, which is element-wise. Then we crushed it again. So we flattened consecutively and ended up with a 4 by 2 by 400 now.

Then linear brought it back down to 200, Bashorm 10h. And lastly, we get a 4 by 400. And we see that the flattened consecutive for the last flattened here, it squeezed out that dimension of one. So we only ended up with 4 by 400. And then linear Bashorm 10h and the last linear layer to get our logits.

And so the logits end up in the same shape as they were before. But now we actually have a nice three-layer neural net. And it basically corresponds to-- whoops, sorry. It basically corresponds exactly to this network now, except only this piece here, because we only have three layers. Whereas here in this example, there's four layers with a total receptive field size of 16 characters instead of just eight characters.

So the block size here is 16. So this piece of it is basically implemented here. Now we just have to figure out some good channel numbers to use here. Now in particular, I changed the number of hidden units to be 68 in this architecture, because when I use 68, the number of parameters comes out to be 22,000.

So that's exactly the same that we had before. And we have the same amount of capacity at this neural net in terms of the number of parameters. But the question is whether we are utilizing those parameters in a more efficient architecture. So what I did then is I got rid of a lot of the debugging cells here, and I reran the optimization.

And scrolling down to the result, we see that we get the identical performance roughly. So our validation loss now is 2.029, and previously it was 2.027. So controlling for the number of parameters, changing from the flat to hierarchical is not giving us anything yet. That said, there are two things to point out.

Number one, we didn't really torture the architecture here very much. This is just my first guess. And there's a bunch of hyperparameter search that we could do in terms of how we allocate our budget of parameters to what layers. Number two, we still may have a bug inside the BashNorm1D layer.

So let's take a look at that, because it runs, but does it do the right thing? So I pulled up the layer inspector that we have here and printed out the shapes along the way. And currently it looks like the BashNorm is receiving an input that is 32 by 4 by 68.

And here on the right, I have the current implementation of BashNorm that we have right now. Now, this BashNorm assumed, in the way we wrote it and at the time, that x is two-dimensional. So it was n by d, where n was the batch size. So that's why we only reduced the mean and the variance over the zeroth dimension.

But now x will basically become three-dimensional. So what's happening inside the BashNorm layer right now, and how come it's working at all and not giving any errors? The reason for that is basically because everything broadcasts properly, but the BashNorm is not doing what we want it to do. So in particular, let's basically think through what's happening inside the BashNorm, looking at what's happening here.

I have the code here. So we're receiving an input of 32 by 4 by 68. And then we are doing here, x dot mean, here I have e instead of x, but we're doing the mean over zero. And that's actually given us 1 by 4 by 68. So we're doing the mean only over the very first dimension.

And it's given us a mean and a variance that still maintain this dimension here. So these means are only taking over 32 numbers in the first dimension. And then when we perform this, everything broadcasts correctly still. But basically what ends up happening is when we also look at the running mean, the shape of it.

So I'm looking at the model dot layers at three, which is the first BashNorm layer, and then looking at whatever the running mean became and its shape. The shape of this running mean now is 1 by 4 by 68. Instead of it being just a size of dimension, because we have 68 channels, we expect to have 68 means and variances that we're maintaining.

But actually, we have an array of 4 by 68. And so basically what this is telling us is this BashNorm is currently working in parallel over 4 times 68 instead of just 68 channels. So basically, we are maintaining statistics for every one of these four positions individually and independently.

And instead, what we want to do is we want to treat this 4 as a Bash dimension, just like the 0th dimension. So as far as the BashNorm is concerned, we don't want to average over 32 numbers, we want to now average over 32 times 4 numbers for every single one of these 68 channels.

So let me now remove this. It turns out that when you look at the documentation of torch.mean, in one of its signatures, when we specify the dimension, we see that the dimension here is not just, it can be int or it can also be a tuple of ints. So we can reduce over multiple integers at the same time, over multiple dimensions at the same time.

So instead of just reducing over 0, we can pass in a tuple, 0, 1, and here 0, 1 as well. And then what's going to happen is the output, of course, is going to be the same. But now what's going to happen is because we reduce over 0 and 1, if we look at in mean.shape, we see that now we've reduced, we took the mean over both the 0th and the 1st dimension.

So we're just getting 68 numbers and a bunch of spurious dimensions here. So now this becomes 1 by 1 by 68, and the running mean and the running variance, analogously, will become 1 by 1 by 68. So even though there are the spurious dimensions, the correct thing will happen in that we are only maintaining means and variances for 68 channels.

And we're now calculating the mean and variance across 32 times 4 dimensions. So that's exactly what we want. And let's change the implementation of BatchNorm1D that we have so that it can take in two-dimensional or three-dimensional inputs and perform accordingly. So at the end of the day, the fix is relatively straightforward.

Basically, the dimension we want to reduce over is either 0 or the tuple 0 and 1, depending on the dimensionality of x. So if x.ndim is 2, so it's a two-dimensional tensor, then the dimension we want to reduce over is just the integer 0. If x.ndim is 3, so it's a three-dimensional tensor, then the dims we're going to assume are 0 and 1 that we want to reduce over.

And then here, we just pass in dim. And if the dimensionality of x is anything else, we'll now get an error, which is good. So that should be the fix. Now I want to point out one more thing. We're actually departing from the API of PyTorch here a little bit.

Because when you come to BatchNorm1D in PyTorch, you can scroll down and you can see that the input to this layer can either be n by c, where n is the batch size and c is the number of features or channels, or it actually does accept three-dimensional inputs, but it expects it to be n by c by l, where l is, say, the sequence length or something like that.

So this is a problem because you see how c is nested here in the middle. And so when it gets three-dimensional inputs, this BatchNorm layer will reduce over 0 and 2 instead of 0 and 1. So basically, PyTorch BatchNorm1D layer assumes that c will always be the first dimension, whereas we assume here that c is the last dimension and there are some number of batch dimensions beforehand.

And so it expects n by c or n by c by l. We expect n by c or n by l by c. And so it's a deviation. I think it's okay. I prefer it this way, honestly, so this is the way that we will keep it for our purposes.

So I redefined the layers, reinitialized the neural nut, and did a single forward pass with a break just for one step. Looking at the shapes along the way, they're of course identical. All the shapes are the same. But the way we see that things are actually working as we want them to now is that when we look at the BatchNorm layer, the running mean shape is now 1 by 1 by 68.

So we're only maintaining 68 means for every one of our channels, and we're treating both the 0th and the first dimension as a batch dimension, which is exactly what we want. So let me retrain the neural net now. Okay, so I've retrained the neural net with the bug fix.

We get a nice curve. And when we look at the validation performance, we do actually see a slight improvement. So it went from 2.029 to 2.022. So basically, the bug inside the BatchNorm was holding us back a little bit, it looks like. And we are getting a tiny improvement now, but it's not clear if this is statistically significant.

And the reason we slightly expect an improvement is because we're not maintaining so many different means and variances that are only estimated using 32 numbers, effectively. Now we are estimating them using 32 times 4 numbers. So you just have a lot more numbers that go into any one estimate of the mean and variance.

And it allows things to be a bit more stable and less wiggly inside those estimates of those statistics. So pretty nice. With this more general architecture in place, we are now set up to push the performance further by increasing the size of the network. So for example, I've bumped up the number of embeddings to 24 instead of 10, and also increased the number of hidden units.

But using the exact same architecture, we now have 76,000 parameters. And the training takes a lot longer, but we do get a nice curve. And then when you actually evaluate the performance, we are now getting validation performance of 1.993. So we've crossed over the 2.0 sort of territory, and we're at about 1.99.

But we are starting to have to wait quite a bit longer. And we're a little bit in the dark with respect to the correct setting of the hyperparameters here and the learning rates and so on, because the experiments are starting to take longer to train. And so we are missing sort of like an experimental harness on which we could run a number of experiments and really tune this architecture very well.

So I'd like to conclude now with a few notes. We basically improved our performance from a starting of 2.1 down to 1.9. But I don't want that to be the focus, because honestly, we're kind of in the dark, we have no experimental harness, we're just guessing and checking. And this whole thing is terrible.

We're just looking at the training loss. Normally, you want to look at both the training and the validation loss together. The whole thing looks different if you're actually trying to squeeze out numbers. That said, we did implement this architecture from the WaveNet paper. But we did not implement this specific forward pass of it, where you have a more complicated linear layer sort of that is this gated linear layer kind of.

And there's residual connections and skip connections and so on. So we did not implement that, we just implemented this structure. I would like to briefly hint or preview how what we've done here relates to convolutional neural networks as used in the WaveNet paper. And basically, the use of convolutions is strictly for efficiency.

It doesn't actually change the model we've implemented. So here, for example, let me look at a specific name to work with an example. So there's a name in our training set, and it's D'Andrea. And it has seven letters, so that is eight independent examples in our model. So all these rows here are independent examples of D'Andrea.

Now, you can forward, of course, any one of these rows independently. So I can take my model and call it on any individual index. Notice, by the way, here, I'm being a little bit tricky. The reason for this is that extra at 7.shape is just one dimensional array of eight.

So you can't actually call the model on it, you're going to get an error, because there's no batch dimension. So when you do extra at list of seven, then the shape of this becomes one by eight. So I get an extra batch dimension of one, and then we can forward the model.

So that forwards a single example. And you might imagine that you actually may want to forward all of these eight at the same time. So pre-allocating some memory and then doing a for loop eight times and forwarding all of those eight here will give us all the logits in all these different cases.

Now, for us with the model as we've implemented it right now, this is eight independent calls to our model. But what convolutions allow you to do is it allow you to basically slide this model efficiently over the input sequence. And so this for loop can be done not outside in Python, but inside of kernels in CUDA.

And so this for loop gets hidden into the convolution. So the convolution basically, you can think of it as it's a for loop, applying a little linear filter over space of some input sequence. And in our case, the space we're interested in is one dimensional, and we're interested in sliding these filters over the input data.

So this diagram actually is fairly good as well. Basically, what we've done is here they are highlighting in black one single sort of like tree of this calculation. So just calculating the single output example here. And so this is basically what we've implemented here. We've implemented a single, this black structure, we've implemented that and calculated a single output, like a single example.

But what convolutions allow you to do is it allows you to take this black structure and kind of like slide it over the input sequence here and calculate all of these orange outputs at the same time. Or here that corresponds to calculating all of these outputs of at all the positions of DeAndre at the same time.

And the reason that this is much more efficient is because number one, as I mentioned, the for loop is inside the CUDA kernels in the sliding. So that makes it efficient. But number two, notice the variable reuse here. For example, if we look at this circle, this node here, this node here is the right child of this node, but it's also the left child of the node here.

And so basically, this node and its value is used twice. And so right now, in this naive way, we'd have to recalculate it. But here we are allowed to reuse it. So in the convolutional neural network, you think of these linear layers that we have up above as filters.

And we take these filters, and they're linear filters, and you slide them over input sequence. And we calculate the first layer, and then the second layer, and then the third layer, and then the output layer of the sandwich. And it's all done very efficiently using these convolutions. So we're going to cover that in a future video.

The second thing I hope you took away from this video is you've seen me basically implement all of these layer Lego building blocks or module building blocks. And I'm implementing them over here. And we've implemented a number of layers together. And we've also implementing these these containers. And we've overall pytorchified our code quite a bit more.

Now, basically, what we're doing here is we're re-implementing torch.nn, which is the neural networks library on top of torch.tensor. And it looks very much like this, except it is much better, because it's in pytorch instead of a janky, lazy, and stupid notebook. So I think going forward, I will probably have considered us having unlocked torch.nn.

We understand roughly what's in there, how these modules work, how they're nested, and what they're doing on top of torch.tensor. So hopefully, we'll just switch over and continue and start using torch.nn directly. The next thing I hope you got a bit of a sense of is what the development process of building deep neural networks looks like, which I think was relatively representative to some extent.

So number one, we are spending a lot of time in the documentation page of pytorch. And we're reading through all the layers, looking at documentations, what are the shapes of the inputs, what can they be, what does the layer do, and so on. Unfortunately, I have to say the pytorch documentation is not very good.

They spend a ton of time on hardcore engineering of all kinds of distributed primitives, etc. But as far as I can tell, no one is maintaining the documentation. It will lie to you, it will be wrong, it will be incomplete, it will be unclear. So unfortunately, it is what it is, and you just kind of do your best with what they've given us.

Number two, the other thing that I hope you got a sense of is there's a ton of trying to make the shapes work. And there's a lot of gymnastics around these multi-dimensional arrays. And are they two dimensional, three dimensional, four dimensional? What layers take what shapes? Is it NCL or NLC?

And you're permuting and viewing, and it just can get pretty messy. And so that brings me to number three. I very often prototype these layers and implementations in Jupyter Notebooks and make sure that all the shapes work out. And I'm spending a lot of time basically babysitting the shapes and making sure everything is correct.

And then once I'm satisfied with the functionality in a Jupyter Notebook, I will take that code and copy paste it into my repository of actual code that I'm training with. And so then I'm working with VS code on the side. So I usually have Jupyter Notebook and VS code.

I develop a Jupyter Notebook, I paste into VS code, and then I kick off experiments from the repo, of course, from the code repository. So that's roughly some notes on the development process of working with neural nets. Lastly, I think this lecture unlocks a lot of potential further lectures, because number one, we have to convert our neural network to actually use these dilated causal convolutional layers.

So implementing the ConvNet. Number two, I'm potentially starting to get into what this means, where are residual connections and skip connections and why are they useful? Number three, as I mentioned, we don't have any experimental harness. So right now I'm just guessing, checking everything. This is not representative of typical deep learning workflows.

You have to set up your evaluation harness, you can kick off experiments, you have lots of arguments that your script can take, you're kicking off a lot of experimentation, you're looking at a lot of plots of training and validation losses, and you're looking at what is working and what is not working.

And you're working on this like population level, and you're doing all these hyperparameter searches. And so we've done none of that so far. So how to set that up and how to make it good, I think is a whole another topic. And number three, we should probably cover recurring neural networks, RNNs, LSTMs, GRUs, and of course, transformers.

So many places to go, and we'll cover that in the future. For now, bye. Sorry, I forgot to say that if you are interested, I think it is kind of interesting to try to beat this number 1.993. Because I really haven't tried a lot of experimentation here, and there's quite a bit of longing fruit potentially to still push this further.

So I haven't tried any other ways of allocating these channels in this neural net. Maybe the number of dimensions for the embedding is all wrong. Maybe it's possible to actually take the original network, which is one hidden layer, and make it big enough and actually beat my fancy hierarchical network.

It's not obvious. That would be kind of embarrassing. If this did not do better, even once you torture it a little bit. Maybe you can read the WaveNet paper and try to figure out how some of these layers work and implement them yourselves using what we have. And of course, you can always tune some of the initialization or some of the optimization and see if you can improve it that way.

So I'd be curious if people can come up with some ways to beat this. And yeah, that's it for now. Bye.