Hello, my name is Andrej and I've been training deep neural networks for a bit more than a decade and in this lecture I'd like to show you what neural network training looks like under the hood. So in particular we are going to start with a blank Jupyter notebook and by the end of this lecture we will define and train a neural net and you'll get to see everything that goes on under the hood and exactly sort of how that works on an intuitive level.

Now specifically what I would like to do is I would like to take you through building of micrograd. Now micrograd is this library that I released on github about two years ago but at the time I only uploaded the source code and you'd have to go in by yourself and really figure out how it works.

So in this lecture I will take you through it step by step and kind of comment on all the pieces of it. So what is micrograd and why is it interesting? Thank you. Micrograd is basically an autograd engine. Autograd is short for automatic gradient and really what it does is it implements back propagation.

Now back propagation is this algorithm that allows you to efficiently evaluate the gradient of some kind of a loss function with respect to the weights of a neural network and what that allows us to do then is we can iteratively tune the weights of that neural network to minimize the loss function and therefore improve the accuracy of the network.

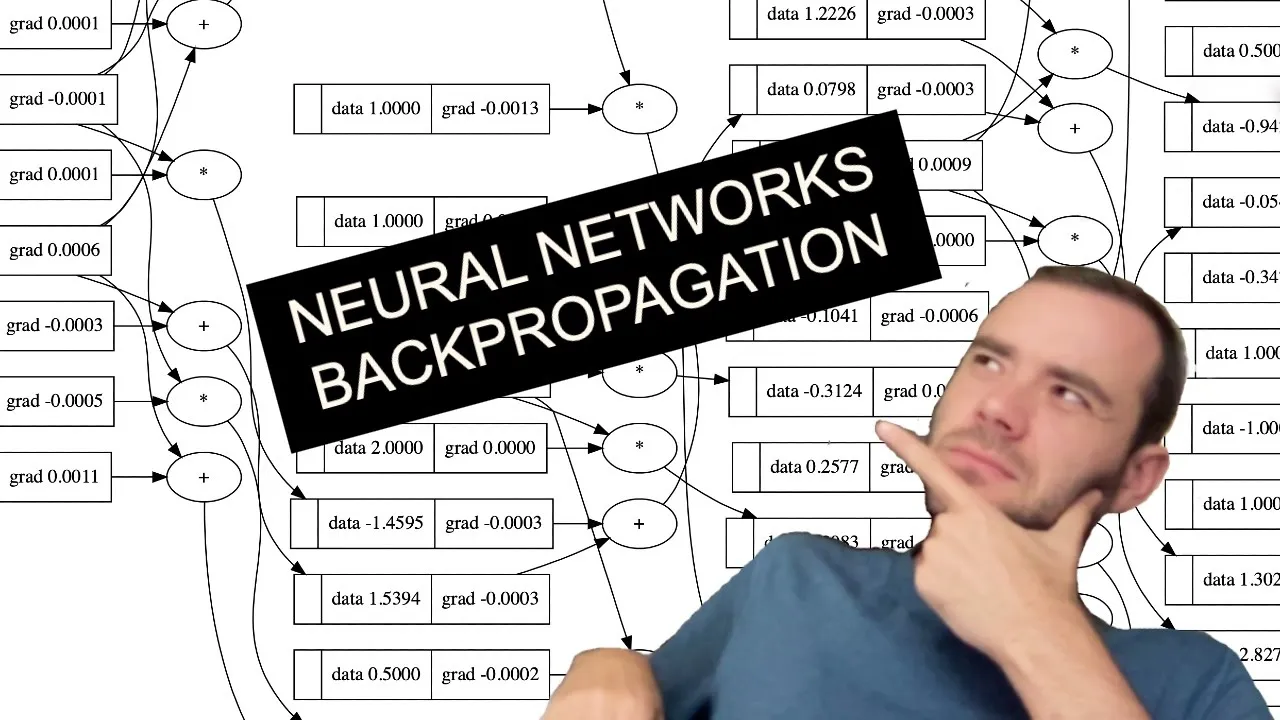
So back propagation would be at the mathematical core of any modern deep neural network library like say pytorch or jax. So the functionality of micrograd is I think best illustrated by an example. So if we just scroll down here you'll see that micrograd basically allows you to build out mathematical expressions and here what we are doing is we have an expression that we're building out where you have two inputs a and b and you'll see that a and b are negative four and two but we are wrapping those values into this value object that we are going to build out as part of micrograd.

So this value object will wrap the numbers themselves and then we are going to build out a mathematical expression here where a and b are transformed into c d and eventually e f and g and I'm showing some of the functionality of micrograd and the operations that it supports.

So you can add two value objects, you can multiply them, you can raise them to a constant power, you can offset by one, negate, squash at zero, square, divide by a constant, divide by it, etc. And so we're building out an expression graph with these two inputs a and b and we're creating an output value of g and micrograd will in the background build out this entire mathematical expression.

So it will for example know that c is also a value, c was a result of an addition operation and the child nodes of c are a and b because the and it will maintain pointers to a and b value objects so we'll basically know exactly how all of this is laid out.

And then not only can we do what we call the forward pass where we actually look at the value of g of course that's pretty straightforward we will access that using the dot data attribute and so the output of the forward pass the value of g is 24.7 it turns out but the big deal is that we can also take this g value object and we can call dot backward and this will basically initialize backpropagation at the node g.

And what backpropagation is going to do is it's going to start at g and it's going to go backwards through that expression graph and it's going to recursively apply the chain rule from calculus and what that allows us to do then is we're going to evaluate basically the derivative of g with respect to all the internal nodes like e d and c but also with respect to the inputs a and b and then we can actually query this derivative of g with respect to a for example that's a dot grad in this case it happens to be 138 and the derivative of g with respect to b which also happens to be here 645 and this derivative we'll see soon is very important information because it's telling us how a and b are affecting g through this mathematical expression so in particular a dot grad is 138 so if we slightly nudge a and make it slightly larger 138 is telling us that g will grow and the slope of that growth is going to be 138 and the slope of growth of b is going to be 645 so that's going to tell us about how g will respond if a and b get tweaked a tiny amount in a positive direction okay um now you might be confused about what this expression is that we built out here and this expression by the way is completely meaningless i just made it up i'm just flexing about the kinds of operations that are supported by micrograd and what we actually really care about are neural networks but it turns out that neural networks are just mathematical expressions just like this one but actually slightly a bit less crazy even neural networks are just a mathematical expression they take the input data as an input and they take the weights of a neural network as an input and it's a mathematical expression and the output are your predictions of your neural net or the loss function we'll see this in a bit but basically neural networks just happen to be a certain class of mathematical expressions but back propagation is actually significantly more general it doesn't actually care about neural networks at all it only tells us about arbitrary mathematical expressions and then we happen to use that machinery for training of neural networks now one more note i would like to make at this stage is that as you see here micrograd is a scalar valued autograd engine so it's working on the you know level of individual scalars like negative four and two and we're taking neural nets and we're breaking them down all the way to these atoms of individual scalars and all the little pluses and times and it's just excessive and so obviously you would never be doing any of this in production it's really just for done for pedagogical reasons because it allows us to not have to deal with these n-dimensional tensors that you would use in modern deep neural network library so this is really done so that you understand and refactor out back propagation and chain rule and understanding of neural training and then if you actually want to train bigger networks you have to be using these tensors but none of the math changes this is done purely for efficiency we are basically taking scalar value all the scalar values we're packaging them up into tensors which are just arrays of these scalars and then because we have these large arrays we're making operations on those large arrays that allows us to take advantage of the parallelism in a computer and all those operations can be done in parallel and then the whole thing runs faster but really none of the math changes and they've done purely for efficiency so i don't think that it's pedagogically useful to be dealing with tensors from scratch and i think and that's why i fundamentally wrote micrograd because you can understand how things work at the fundamental level and then you can speed it up later okay so here's the fun part my claim is that micrograd is what you need to train your own networks and everything else is just efficiency so you'd think that micrograd would be a very complex piece of code and that turns out to not be the case so if we just go to micrograd and you'll see that there's only two files here in micrograd this is the actual engine it doesn't know anything about neural nets and this is the entire neural nets library on top of micrograd so engine and nn.py so the actual back propagation autograd engine that gives you the power of neural networks is literally 100 lines of code of like very simple python which we'll understand by the end of this lecture and then nn.py this neural network library built on top of the autograd engine is like a joke it's like we have to define what is a neuron and then we have to define what is a layer of neurons and then we define what is a multilayer perceptron which is just a sequence of layers of neurons and so it's just a total joke so basically there's a lot of power that comes from only 150 lines of code and that's all you need to understand to understand neural network training and everything else is just efficiency and of course there's a lot to efficiency but fundamentally that's all that's happening okay so now let's dive right in and implement micrograd step by step the first thing i'd like to do is i'd like to make sure that you have a very good understanding intuitively of what a derivative is and exactly what information it gives you so let's start with some basic imports that i copy paste in every jupyter notebook always and let's define a function a scalar valid function f of x as follows so i just made this up randomly i just wanted a scalar valid function that takes a single scalar x and returns a single scalar y and we can call this function of course so we can pass and say 3.0 and get 20 back now we can also plot this function to get a sense of its shape you can tell from the mathematical expression that this is probably a parabola it's a quadratic and so if we just create a set of um um scalar values that we can feed in using for example a range from negative 5 to 5 in steps of 0.25 so this is so x is is just from negative 5 to 5 not including 5 in steps of 0.25 and we can actually call this function on this numpy array as well so we get a set of y's if we call f on x's and these y's are basically also applying the function on every one of these elements independently and we can plot this using mathplotlib so plt.plot x's and y's and we get a nice parabola so previously here we fed in 3.0 somewhere here and we received 20 back which is here the y coordinate so now i'd like to think through what is the derivative of this function at any single input point x right so what is the derivative at different points x of this function now if you remember back to your calculus class you've probably derived derivatives so we take this mathematical expression 3x squared minus 4x plus 5 and you would write out on a piece of paper and you would you know apply the product rule and all the other rules and derive the mathematical expression of the great derivative of the original function and then you could plug in different taxes and see what the derivative is we're not going to actually do that because no one in neural networks actually writes out the expression for the neural net it would be a massive expression it would be you know thousands tens of thousands of terms no one actually derives the derivative of course and so we're not going to take this kind of like symbolic approach instead what i'd like to do is i'd like to look at the definition of derivative and just make sure that we really understand what the derivative is measuring what it's telling you about the function and so if we just look up derivative we see that um okay so this is not a very good definition of derivative this is a definition of what it means to be differentiable but if you remember from your calculus it is the limit as h goes to zero of f of x plus h minus f of x over h so basically what it's saying is if you slightly bump up you're at some point x that you're interested in or a and if you slightly bump up you know you slightly increase it by a small number h how does the function respond with what sensitivity does it respond where is the slope at that point does the function go up or does it go down and by how much and that's the slope of that function the the slope of that response at that point and so we can basically evaluate the derivative here numerically by taking a very small h of course the definition would ask us to take h to zero we're just going to pick a very small h 0.001 and let's say we're interested in 0.3.0 so we can look at f of x of course as 20 and now f of x plus h so if we slightly nudge x in a positive direction how is the function going to respond and just looking at this do you expand do you expect f of x plus h to be slightly greater than 20 or do you expect to be slightly lower than 20 and since this 3 is here and this is 20 if we slightly go positively the function will respond positively so you'd expect this to be slightly greater than 20 and now by how much is telling you the sort of the the strength of that slope right the the size of the slope so f of x plus h minus f of x this is how much the function responded in the positive direction and we have to normalize by the run so we have the rise over run to get the slope so this of course is just a numerical approximation of the slope because we have to make h very very small to converge to the exact amount now if i'm doing too many zeros at some point i'm going to get an incorrect answer because we're using floating point arithmetic and the representations of all these numbers in computer memory is finite and at some point we're getting into trouble so we can converge towards the right answer with this approach but basically at 3 the slope is 14 and you can see that by taking 3x squared minus 4x plus 5 and differentiating it in our head so 3x squared would be 6x minus 4 and then we plug in x equals 3 so that's 18 minus 4 is 14 so this is correct so that's at 3 now how about the slope at say negative 3 would you expect what would you expect for the slope now telling the exact value is really hard but what is the sign of that slope so at negative 3 if we slightly go in the positive direction at x the function would actually go down and so that tells you that the slope would be negative so we'll get a slight number below 20 and so if we take the slope we expect something negative negative 22 okay and at some point here of course the slope would be zero now for this specific function i looked it up previously and it's at point 2 over 3 so at roughly 2 over 3 that's somewhere here this derivative would be zero so basically at that precise point yeah at that precise point if we nudge in a positive direction the function doesn't respond this stays the same almost and so that's why the slope is zero okay now let's look at a bit more complex case so we're going to start you know complexifying a bit so now we have a function here with output variable b that is a function of three scalar inputs a b and c so a b and c are some specific values three inputs into our expression graph and a single output d and so if we just print d we get four and now what i'd like to do is i'd like to again look at the derivatives of d with respect to a b and c and think through again just the intuition of what this derivative is telling us so in order to evaluate this derivative we're going to get a bit hacky here we're going to again have a very small value of h and then we're going to fix the inputs at some values that we're interested in so these are the this is the point a b c at which we're going to be evaluating the derivative of d with respect to all a b and c at that point so there are the inputs and now we have d1 is that expression and then we're going to for example look at the derivative of d with respect to a so we'll take a and we'll bump it by h and then we'll get d2 to be the exact same function and now we're going to print um you know f1 d1 is d1 d2 is d2 and print slope so the derivative or slope here will be um of course d2 minus d1 divide h so d2 minus d1 is how much the function increased when we bumped the uh the specific input that we're interested in by a tiny amount and this is the normalized by h to get the slope so um yeah so this so i just run this we're going to print d1 which we know is four now d2 will be bumped a will be bumped by h so let's just think through a little bit what d2 will be uh printed out here in particular d1 will be four will d2 be a number slightly greater than four or slightly lower than four and that's going to tell us the the the sign of the derivative so we're bumping a by h b is minus three c is 10 so you can just intuitively think through this derivative and what it's doing a will be slightly more positive and but b is a negative number so if a is slightly more positive because b is negative three we're actually going to be adding less to d so you'd actually expect that the value of the function will go down so let's just see this yeah and so we went from four to 3.9996 and that tells you that the slope will be negative and then um will be a negative number because we went down and then the exact number of slope will be exact amount of slope is negative three and you can also convince yourself that negative three is the right answer uh mathematically and analytically because if you have a times b plus c and you are you know you have calculus then uh differentiating a times b plus c with respect to a gives you just b and indeed the value of b is negative three which is the derivative that we have so you can tell that that's correct so now if we do this with b so if we bump b by a little bit in a positive direction we'd get different slopes so what is the influence of b on the output d so if we bump b by a tiny amount in a positive direction then because a is positive we'll be adding more to d right so um and now what is the what is the sensitivity what is the slope of that addition and it might not surprise you that this should be two and why is it two because d of d by db differentiating with respect to b would be would give us a and the value of a is two so that's also working well and then if c gets bumped a tiny amount in h by h then of course a times b is unaffected and now c becomes slightly bit higher what does that do to the function it makes it slightly bit higher because we're simply adding c and it makes it slightly bit higher by the exact same amount that we added to c and so that tells you that the slope is one that will be the the rate at which d will increase as we scale c okay so we now have some intuitive sense of what this derivative is telling you about the function and we'd like to move to neural networks now as i mentioned neural networks will be pretty massive expressions mathematical expressions so we need some data structures that maintain these expressions and that's what we're going to start to build out now so we're going to build out this value object that i showed you in the readme page of micrograd so let me copy paste a skeleton of the first very simple value object so class value takes a single scalar value that it wraps and keeps track of and that's it so we can for example do value of 2.0 and then we can get we can look at its content and python will internally use the wrapper function to return this string oops like that so this is a value object with data equals two that we're creating here now we'd like to do is like we'd like to be able to have not just like two values but we'd like to do a plus b right we'd like to add them so currently you would get an error because python doesn't know how to add two value objects so we have to tell it so here's addition so you have to basically use these special double underscore methods in python to define these operators for these objects so if we call um the uh if we use this plus operator python will internally call a dot add of b that's what will happen internally and so b will be the other and self will be a and so we see that what we're going to return is a new value object and it's just uh it's going to be wrapping the plus of their data but remember now because data is the actual like numbered python number so this operator here is just the typical floating point plus addition now it's not an addition of value objects and we'll return a new value so now a plus b should work and it should print value of negative one because that's two plus minus three there we go okay let's now implement multiply just so we can recreate this expression here so multiply i think it won't surprise you will be fairly similar so instead of add we're going to be using mul and then here of course we want to do times and so now we can create a c value object which will be 10.0 and now we should be able to do a times b well let's just do a times b first um that's value of negative six now and by the way i skipped over this a little bit uh suppose that i didn't have the wrapper function here uh then it's just that you'll get some kind of an ugly expression so what wrapper is doing is it's providing us a way to print out like a nicer looking expression in python uh so we don't just have something cryptic we actually are you know it's value of negative six so this gives us a times and then this we should now be able to add c to it because we've defined and told the python how to do mul and add and so this will call this will basically be equivalent to a dot mul of b and then this new value object will be dot add of c and so let's see if that worked yep so that worked well that gave us four which is what we expect from before and i believe you can just call them manually as well there we go so yeah okay so now what we are missing is the connected tissue of this expression as i mentioned we want to keep these expression graphs so we need to know and keep pointers about what values produce what other values so here for example we are going to introduce a new variable which we'll call children and by default it will be an empty tuple and then we're actually going to keep a slightly different variable in the class which we'll call underscore prev which will be the set of children this is how i done i did it in the original micrograd looking at my code here i can't remember exactly the reason i believe it was efficiency but this underscore children will be a tuple for convenience but then when we actually maintain it in the class it will be just this set i believe for efficiency so now when we are creating a value like this with a constructor children will be empty and prep will be the empty set but when we are creating a value through addition or multiplication we're going to feed in the children of this value which in this case is self and other so those are the children here so now we can do d dot prev and we'll see that the children of the we now know are this a value of negative six and value of 10 and this of course is the value resulting from a times b and the c value which is 10 now the last piece of information we don't know so we know now the children of every single value but we don't know what operation created this value so we need one more element here let's call it underscore up and by default this is the empty set for leaves and then we'll just maintain it here and now the operation will be just a simple string and in the case of addition it's plus in the case of multiplication it's times so now we not just have d dot prep we also have a d dot up and we know that d was produced by an addition of those two values and so now we have the full mathematical expression and we're building out this data structure and we know exactly how each value came to be by what expression and from what other values now because these expressions are about to get quite a bit larger we'd like a way to nicely visualize these expressions that we're building out so for that i'm going to copy paste a bunch of slightly scary code that's going to visualize this these expression graphs for us so here's the code and i'll explain it in a bit but first let me just show you what this code does basically what it does is it creates a new function draw dot that we can call on some root node and then it's going to visualize it so if we call draw dot on d which is this final value here that is a times b plus c it creates something like this so this is d and you see that this is a times b creating an integer value plus c gives us this output node d so that's draw dot of b and i'm not going to go through this in complete detail you can take a look at graphvis and its api graphvis is a open source graph visualization software and what we're doing here is we're building out this graph in graphvis api and you can basically see that trace is this helper function that enumerates all the nodes and edges in the graph so that just builds a set of all the nodes and edges and then we iterate through all the nodes and we create special node objects for them in using dot node and then we also create edges using dot dot edge and the only thing that's like slightly tricky here is you'll notice that i basically add these fake nodes which are these operation nodes so for example this node here is just like a plus node and i create these special op nodes here and i connect them accordingly so these nodes of course are not actual nodes in the original graph they're not actually a value object the only value objects here are the things in squares those are actual value objects or representations thereof and these op nodes are just created in this draw dot routine so that it looks nice let's also add labels to these graphs just so we know what variables are where so let's create a special underscore label or let's just do label equals empty by default and save it in each node and then here we're going to do label as a label is b label is c and then let's create a special e equals a times b and e dot label will be e it's kind of naughty and e will be e plus c and a d dot label will be b okay so nothing really changes i just added this new e function that new e variable and then here when we are printing this i'm going to print the label here so this will be a percent s bar and this will be n dot label and so now we have the label on the left here so it says a b creating e and then e plus c creates d just like we have it here and finally let's make this expression just one layer deeper so d will not be the final output node instead after d we are going to create a new value object called f we're going to start running out of variables soon f will be negative 2.0 and its label will of course just be f and then L capital L will be the output of our graph and L will be d times f okay so L will be negative 8 is the output so now we don't just draw a d we draw L okay and somehow the label of L is undefined oops all that label has to be explicitly sort of given to it there we go so L is the output so let's quickly recap what we've done so far we are able to build out mathematical expressions using only plus and times so far they are scalar valued along the way and we can do this forward pass and build out a mathematical expression so we have multiple inputs here a b c and f going into a mathematical expression that produces a single output L and this here is visualizing the forward pass so the output of the forward pass is negative 8 that's the value now what we'd like to do next is we'd like to run back propagation and in back propagation we are going to start here at the end and we're going to reverse and calculate the gradient along along all these intermediate values and really what we're computing for every single value here we're going to compute the derivative of that node with respect to L so the derivative of L with respect to L is just one and then we're going to derive what is the derivative of L with respect to f with respect to d with respect to c with respect to e with respect to b and with respect to a and in a neural network setting you'd be very interested in the derivative of basically this loss function L with respect to the weights of a neural network and here of course we have just these variables a b c and f but some of these will eventually represent the weights of a neural net and so we'll need to know how those weights are impacting the loss function so we'll be interested basically in the derivative of the output with respect to some of its leaf nodes and those leaf nodes will be the weights of the neural net and the other leaf nodes of course will be the data itself but usually we will not want or use the derivative of the loss function with respect to data because the data is fixed but the weights will be iterated on using the gradient information so next we are going to create a variable inside the value class that maintains the derivative of L with respect to that value and we will call this variable grad so there's a dot data and there's a self dot grad and initially it will be zero and remember that zero is basically means no effect so at initialization we're assuming that every value does not impact does not affect the output right because if the gradient is zero that means that changing this variable is not changing the loss function so by default we assume that the gradient is zero and then now that we have grad and it's you know 0.0 we are going to be able to visualize it here after data so here grad is 0.4f and this will be in dot grad and now we are going to be showing both the data and the grad initialized at zero and we are just about getting ready to calculate the back propagation and of course this grad again as I mentioned is representing the derivative of the output in this case L with respect to this value so with respect to so this is the derivative of L with respect to f with respect to d and so on so let's now fill in those gradients and actually do back propagation manually so let's start filling in these gradients and start all the way at the end as I mentioned here first we are interested to fill in this gradient here so what is the derivative of L with respect to L in other words if I change L by a tiny amount h how much does L change it changes by h so it's proportional and therefore the derivative will be one we can of course measure these or estimate these numerical gradients numerically just like we've seen before so if I take this expression and I create a def lol function here and put this here now the reason I'm creating a gating function lol here is because I don't want to pollute or mess up the global scope here this is just kind of like a little staging area and as you know in Python all of these will be local variables to this function so I'm not changing any of the global scope here so here L1 will be L and then copy pasting this expression we're going to add a small amount h and for example a right and this would be measuring the derivative of L with respect to a so here this will be L2 and then we want to print that derivative so print L2 minus L1 which is how much L changed and then normalize it by h so this is the rise over run and we have to be careful because L is a value node so we actually want its data so that these are floats dividing by h and this should print the derivative of L with respect to a because a is the one that we bumped a little bit by h so what is the derivative of L with respect to a it's six okay and obviously if we change L by h then that would be here effectively this looks really awkward but changing L by h you see the derivative here is one that's kind of like the base case of what we are doing here so basically we can come up here and we can manually set L.grad to one this is our manual back propagation L.grad is one and let's redraw and we'll see that we filled in grad is one for L we're now going to continue the back propagation so let's here look at the derivatives of L with respect to D and F let's do a D first so what we are interested in if I create a markdown on here is we'd like to know basically we have that L is D times F and we'd like to know what is D L by D D what is that and if you know your calculus L is D times F so what is D L by D D it would be F and if you don't believe me we can also just derive it because the proof would be fairly straightforward we go to the definition of the derivative which is F of x plus h minus F of x divide h as a limit limit of h goes to zero of this kind of expression so when we have L is D times F then increasing D by h would give us the output of D plus h times F that's basically F of x plus h right minus D times F and then divide h and symbolically expanding out here we would have basically D times F plus h times F minus D times F divide h and then you see how the D F minus D F cancels so you're left with h times F divide h which is F so in the limit as h goes to zero of you know derivative definition we just get F in the case of D times F so symmetrically D L by D F will just be D so what we have is that F dot grad we see now is just the value of D which is four and we see that D dot grad is just the value of F and so the value of F is negative two so we'll set those manually let me erase this markdown node and then let's redraw what we have okay and let's just make sure that these were correct so we seem to think that D L by D D is negative two so let's double check um let me erase this plus h from before and now we want the derivative with respect to F so let's just come here when I create F and let's do a plus h here and this should print a derivative of L with respect to F so we expect to see four yeah and this is four up to floating point funkiness and then D L by D D should be F which is negative two grad is negative two so if we again come here and we change D D dot data plus equals h right here so we expect so we've added a little h and then we see how L changed and we expect to print negative two there we go so we've numerically verified what we're doing here is kind of like an inline gradient check gradient check is when we are deriving this like back propagation and getting the derivative with respect to all the intermediate results and then numerical gradient is just you know um estimating it using small step size now we're getting to the crux of back propagation so this will be the most important node to understand because if you understand the gradient for this node you understand the gradient for this node because if you understand the gradient for this node you understand all of back propagation and all of training of neural nets basically so we need to derive D L by D C in other words the derivative of L with respect to C because we've computed all these other gradients already now we're coming here and we're continuing the back propagation manually so we want D L by D C and we'll also derive D L by D E now here's the problem how do we derive D L by D C we actually know the derivative L with respect to D so we know how L is sensitive to D but how is L sensitive to C so if we wiggle C how does that impact L through D so we know D L by D C and we also here know how C impacts D and so just very intuitively if you know the impact that C is having on D and the impact that D is having on L then you should be able to somehow put that information together to figure out how C impacts L and indeed this is what we can actually do so in particular we know just concentrating on D first let's look at how what is the derivative basically of D with respect to C so in other words what is D D by D C so here we know that D is C times C plus E that's what we know and now we're interested in D D by D C if you just know your calculus again and you remember then differentiating C plus E with respect to C you know that that gives you 1.0 and we can also go back to the basics and derive this because again we can go to our f of x plus h minus f of x divide by h that's the definition of a derivative as h goes to zero and so here focusing on C and its effect on D we can basically do the f of x plus h will be C is incremented by h plus E that's the first evaluation of our function minus C plus E and then divide h and so what is this just expanding this out this will be C plus h plus C minus C minus E divide h and then you see here how C minus C cancels E minus E cancels we're left with h over h which is 1.0 and so by symmetry also D D by D E will be 1.0 as well so basically the derivative of a sum expression is very simple and this is the local derivative so I call this the local derivative because we have the final output value all the way at the end of this graph and we're now like a small node here and this is a little plus node and it the little plus node doesn't know anything about the rest of the graph that it's embedded in all it knows is that it did plus it took a C and an E added them and created D and this plus node also knows the local influence of C on D or rather the derivative of D with respect to C and it also knows the derivative of D with respect to E but that's not what we want that's just the local derivative what we actually want is D L by D C and L is here just one step away but in the general case this little plus node could be embedded in like a massive graph so again we know how L impacts D and now we know how C and E impact D how do we put that information together to write D L by D C and the answer of course is the chain rule in calculus and so I pulled up chain rule here from Wikipedia and I'm going to go through this very briefly so chain rule Wikipedia sometimes can be very confusing and calculus can be very confusing like this is the way I learned chain rule and it was very confusing like what is happening it's just complicated so I like this expression much better if a variable Z depends on a variable Y which itself depends on a variable X then Z depends on X as well obviously through the intermediate variable Y and in this case the chain rule is expressed as if you want D Z by D X then you take the D Z by D Y and you multiply it by D Y by D X so the chain rule fundamentally is telling you how we chain these derivatives together correctly so to differentiate through a function composition we have to apply a multiplication of those derivatives so that's really what chain rule is telling us and there's a nice little intuitive explanation here which I also think is kind of cute the chain rule states that knowing the instantaneous rate of change of Z with respect to Y and Y relative to X allows one to calculate the instantaneous rate of change of Z relative to X as a product of those two rates of change simply the product of those two so here's a good one if a car travels twice as fast as a bicycle and the bicycle is four times as fast as walking men then the car travels two times four eight times as fast as the man and so this makes it very clear that the correct thing to do sort of is to multiply so car is twice as fast as bicycle and bicycle is four times as fast as man so the car will be eight times as fast as the man and so we can take these intermediate rates of change if you will and multiply them together and that justifies the chain rule intuitively so have a look at chain rule but here really what it means for us is there's a very simple recipe for deriving what we want which is dL by dc and what we have so far is we know want and we know what is the impact of d on L so we know dL by dd the derivative of L with respect to dd we know that that's negative two and now because of this local reasoning that we've done here we know dd by dc so how does c impact d and in particular this is a plus node so the local derivative is simply 1.0 it's very simple and so the chain rule tells us that dL by dc going through this intermediate variable will just be simply dL by dd times dd by dc that's chain rule so this is identical to what's happening here except z is our L y is our d and x is our c so we literally just have to multiply these and because these local derivatives like dd by dc are just one we basically just copy over dL by dd because this is just times one so what does it do so because dL by dd is negative two what is dL by dc well it's the local gradient 1.0 times dL by dd which is negative two so literally what a plus node does you can look at it that way is it literally just routes the gradient because the plus nodes local derivatives are just one and so in the chain rule one times dL by dd is just dL by dd and so that derivative just gets routed to both c and to e in this case so basically we have that e dot grad or let's start with c since that's the one we've looked at is negative two times one negative two and in the same way by symmetry e dot grad will be negative two that's the claim so we can set those we can redraw and you see how we just assign negative two negative two so this back propagating signal which is carrying the information of like what is the derivative of L with respect to all the intermediate nodes we can imagine it almost like flowing backwards through the graph and a plus node will simply distribute the derivative to all the leaf nodes sorry to all the children nodes of it so this is the claim and now let's verify it so let me remove the plus h here from before and now instead what we're going to do is we want to increment c so c dot data will be incremented by h and when I run this we expect to see negative two negative two and then of course for e so e dot data plus equals h and we expect to see negative two simple so those are the derivatives of these internal nodes and now we're going to recurse our way backwards again and we're again going to apply the chain rule so here we go our second application of chain rule and we will apply it all the way through the graph we just happen to only have one more node remaining we have that dl by de as we have just calculated is negative two so we know that so we know the derivative of l with respect to e and now we want dl by da right and the chain rule is telling us that that's just dl by de times the local gradient so what is the local gradient basically de by da we have to look at that so i'm a little times node inside a massive graph and i only know that i did a times b and i produced an e so now what is de by da and de by db that's the only thing that i sort of know about that's my local gradient so because we have that e is a times b we're asking what is de by da and of course we just did that here we had a times so i'm not going to re-derive it but if you want to differentiate this with respect to a you'll just get b right the value of b which in this case is negative 3.0 so basically we have that dl by da well let me just do it right here we have that a dot grad and we are applying chain rule here is dl by de which we see here is negative two times what is de by da it's the value of b which is negative three that's it and then we have b dot grad is again dl by de which is negative two just the same way times what is de by d db is the value of a which is 2.0 that's the value of a so these are our claimed derivatives let's redraw and we see here that a dot grad turns out to be six because that is negative two times negative three and b dot grad is negative four times sorry is negative two times two which is negative four so those are our claims let's delete this and let's verify them we have a here a dot data plus equals h so the claim is that a dot grad is six let's verify six and we have b dot data plus equals h so nudging b by h and looking at what happens we claim it's negative four and indeed it's negative four plus minus again float oddness and that's it this that was the manual back propagation all the way from here to all the leaf nodes and we've done it piece by piece and really all we've done is as you saw we iterated through all the nodes one by one and locally applied the chain rule we also applied the one and locally applied the chain rule we always know what is the derivative of l with respect to this little output and then we look at how this output was produced this output was produced through some operation and we have the pointers to the children nodes of this operation and so in this little operation we know what the local derivatives are and we just multiply them onto the derivative always so we just go through and recursively multiply on the local derivatives and that's what back propagation is it's just a recursive application of chain rule backwards through the computation graph let's see this power in action just very briefly what we're going to do is we're going to nudge our inputs to try to make l go up so in particular what we're doing is we want a dot data we're going to change it and if we want l to go up that means we just have to go in the direction of the gradient so a should increase in the direction of gradient by like some small step amount this is the step size and we don't just want this for b but also for b also for c also for f those are leaf nodes which we usually have control over and if we nudge in direction of the gradient we expect a positive influence on l so we expect l to go up positively so it should become less negative it should go up to say negative you know six or something like that it's hard to tell exactly and we'd have to rerun the forward pass so let me just do that here this would be the forward pass f would be unchanged this is effectively the forward pass and now if we print l dot data we expect because we nudged all the values all the inputs in the direction of gradient we expected less negative l we expect it to go up so maybe it's negative six or so let's see what happens okay negative seven and this is basically one step of an optimization that will end up running and really this gradient just give us some power because we know how to influence the final outcome and this will be extremely useful for training neural nets as well as cnc so now i would like to do one more example of manual back propagation using a bit more complex and useful example we are going to back propagate through a neuron so we want to eventually build up neural networks and in the simplest case these are multi-layer perceptrons as they're called so this is a two-layer neural net and it's got these hidden layers made up of neurons and these neurons are fully connected to each other now biologically neurons are very complicated devices but we have very simple mathematical models of them and so this is a very simple mathematical model of a neuron you have some inputs x's and then you have these synapses that have weights on them so the w's are weights and then the synapse interacts with the input to this neuron multiplicatively so what flows to the cell body of this neuron is w times x but there's multiple inputs so there's many w times x's flowing to the cell body the cell body then has also like some bias so this is kind of like the in innate sort of trigger happiness of this neuron so this bias can make it a bit more trigger happy or a bit less trigger happy regardless of the input but basically we're taking all the w times x of all the inputs adding the bias and then we take it through an activation function and this activation function is usually some kind of a squashing function like a sigmoid or 10h or something like that so as an example we're going to use the 10h in this example numpy has a np.10h so we can call it on a range and we can plot it this is the 10h function and you see that the inputs as they come in get squashed on the y coordinate here so right at zero we're going to get exactly zero and then as you go more positive in the input then you'll see that the function will only go up to one and then plateau out and so if you pass in very positive inputs we're going to cap it smoothly at one and on the negative side we're going to cap it smoothly to negative one so that's 10h and that's the squashing function or an activation function and what comes out of this neuron is just the activation function applied to the dot product of the weights and the inputs so let's write one out i'm going to copy paste because i don't want to type too much but okay so here we have the inputs x1 x2 so this is a two-dimensional neuron so two inputs are going to come in these are thought of as the weights of this neuron weights w1 w2 and these weights again are the synaptic strengths for each input and this is the bias of the neuron b and now what we want to do is according to this model we need to multiply x1 times w1 and x2 times w2 and then we need to add bias on top of it and it gets a little messy here but all we are trying to do is x1 w1 plus x2 w2 plus b and these are multiplied here except i'm doing it in small steps so that we actually have pointers to all these intermediate nodes so we have x1 w1 variable x times x2 w2 variable and i'm also labeling them so n is now the cell body raw activation without the activation function for now and this should be enough to basically plot it so draw dot of n gives us x1 times w1 x2 times w2 being added then the bias gets added on top of this and this n is this sum so we're now going to take it through an activation function and let's say we use the tan h so that we produce the output so what we'd like to do here is we'd like to do the output and i'll call it o is n dot tan h okay but we haven't yet written the tan h now the reason that we need to implement another tan h function here is that tan h is a hyperbolic function and we've only so far implemented plus and the times and you can't make a tan h out of just pluses and times you also need exponentiation so tan h is this kind of a formula here you can use either one of these and you see that there's exponentiation involved which we have not implemented yet for our low value node here so we're not going to be able to produce tan h yet and we have to go back up and implement something like it now one option here is we could actually implement exponentiation right and we could return the exp of a value instead of a tan h of a value because if we had exp then we have everything else that we need so because we know how to add and we know how to we know how to add and we know how to multiply so we'd be able to create tan h if we knew how to exp but for the purposes of this example i specifically wanted to show you that we don't necessarily need to have the most atomic pieces in this value object we can actually like create functions at arbitrary points of abstraction they can be complicated functions but they can be also very very simple functions like a plus and it's totally up to us the only thing that matters is that we know how to differentiate through any one function so we take some inputs and we make an output the only thing that matters it can be arbitrarily complex function as long as you know how to create the local derivative if you know the local derivative of how the inputs impact the output then that's all you need so we're going to cluster up all of this expression and we're not going to break it down to its atomic pieces we're just going to directly implement tan h so let's do that dev tan h and then out will be a value of and we need this expression here so um let me actually copy paste let's grab n which is a sub theta and then this i believe is the tan h math.exp of two no n minus one over two n plus one maybe i can call this x just so that it matches exactly okay and now this will be t and uh children of this node there's just one child and i'm wrapping it in a tuple so this is a tuple of one object just self and here the name of this operation will be tan h and we're going to return that okay so now value should be implementing tan h and now we can scroll all the way down here and we can actually do n dot tan h and that's going to return the tan h output of n and now we should be able to draw dot of o not of n so let's see how that worked there we go n went through tan h to produce this output so now tan h is a sort of uh our little micro grad supported node here as an operation and as long as we know the derivative of tan h then we'll be able to back propagate through it now let's see this tan h in action currently it's not squashing too much because the input to it is pretty low so the bias was increased to say eight then we'll see that what's flowing into the tan h now is two and tan h is squashing it to 0.96 so we're already hitting the tail of this tan h and it will sort of smoothly go up to one and then plateau out over there okay so now i'm going to do something slightly strange i'm going to change this bias from eight to this number 6.88 etc and i'm going to do this for specific reasons because we're about to start back propagation and i want to make sure that our numbers come out nice they're not like very crazy numbers they're nice numbers that we can sort of understand in our head let me also add those label o is short for output here so that's the r okay so 0.88 flows into tan h comes out 0.7 so on so now we're going to do back propagation and we're going to fill in all the gradients so what is the derivative o with respect to all the inputs here and of course in a typical neural network setting what we really care about the most is the derivative of these neurons on the weights specifically the w2 and w1 because those are the weights that we're going to be changing part of the optimization and the other thing that we have to remember is here we have only a single neuron but in the neural net you typically have many neurons and they're connected so this is only like a one small neuron a piece of a much bigger puzzle and eventually there's a loss function that sort of measures the accuracy of the neural net and we're back propagating with respect to that accuracy and trying to increase it so let's start off back propagation here and what is the derivative of o with respect to o the base case sort of we know always is that the gradient is just 1.0 so let me fill it in and then let me split out the drawing function here and then here cell clear this output here okay so now when we draw o we'll see that o that grad is 1 so now we're going to back propagate through the tan h so to back propagate through tan h we need to know the local derivative of tan h so if we have that o is tan h of n then what is do by dn now what you could do is you could come here and you could take this expression and you could do your calculus derivative taking and that would work but we can also just scroll down wikipedia here into a section that hopefully tells us that derivative d by dx of tan h of x is any of these i like this one 1 minus tan h square of x so this is 1 minus tan h of x squared so basically what this is saying is that do by dn is 1 minus tan h of n squared and we already have tan h of n it's just o so it's 1 minus o squared so o is the output here so the output is this number o dot data is this number and then what this is saying is that do by dn is 1 minus this squared so 1 minus o dot data squared is 0.5 conveniently so the local derivative of this tan h operation here is 0.5 and so that would be do by dn so we can fill in that n dot grad is 0.5 we'll just fill it in so this is exactly 0.5 one half so now we're going to continue the back propagation this is 0.5 and this is a plus node so how is backprop going to what is backprop going to do here and if you remember our previous example a plus is just a distributor of gradient so this gradient will simply flow to both of these equally and that's because the local derivative of this operation is one for every one of its nodes so one times 0.5 is 0.5 so therefore we know that this node here which we called this it's grad it's just 0.5 and we know that b dot grad is also 0.5 so let's set those and let's draw so those are 0.5 continuing we have another plus 0.5 again we'll just distribute so 0.5 will flow to both of these so we can set theirs x2 w2 as well dot grad is 0.5 and let's redraw pluses are my favorite uh operations to back propagate through because it's very simple so now what's flowing into these expressions is 0.5 and so really again keep in mind what the derivative is telling us at every point in time along here this is saying that if we want the output of this neuron to increase then the influence on these expressions is positive on the output both of them are positive contribution to the output so now back propagating to x1 w2 first this is a times node so we know that the local derivative is you know the other term so if we want to calculate x2 dot grad then can you think through what it's going to be so x2 dot grad will be w2 dot data times this x2 w2 dot grad right and w2 dot grad will be x2 dot data times x2 w2 dot grad right so that's the little local piece of chain rule let's set them and let's redraw so here we see that the gradient on our weight 2 is 0 because x2's data was 0 right but x2 will have the gradient 0.5 because data here was 1 and so what's interesting here right is because the input x2 was 0 then because of the way the times works of course this gradient will be 0 and think about intuitively why that is derivative always tells us the influence of this on the final output if i wiggle w2 how is the output changing it's not changing because we're multiplying by 0 so because it's not changing there is no derivative and 0 is the correct answer because we're squashing that 0 and let's do it here 0.5 should come here and flow through this times and so we'll have that x1 dot grad is can you think through a little bit what what this should be the local derivative of times with respect to x1 is going to be w1 so w1's data times x1 w1 dot grad and w1 dot grad will be x1 dot data times x1 w2 w1 dot grad let's see what those came out to be so this is 0.5 so this would be negative 1.5 and this would be 1 and we've back propagated through this expression these are the actual final derivatives so if we want this neuron's output to increase we know that what's necessary is that w2 we have no gradient w2 doesn't actually matter to this neuron right now but this neuron this weight should go up so if this weight goes up then this neuron's output would have gone up and proportionally because the gradient is 1 okay so doing the back propagation manually is obviously ridiculous so we are now going to put an end to this suffering and we're going to see how we can implement the backward pass a bit more automatically we're not going to be doing all of it manually out here it's now pretty obvious to us by example how these pluses and times are back propagating gradients so let's go up to the value object and we're going to start codifying what we've seen in the examples below so we're going to do this by storing a special self.backward and underscore backward and this will be a function which is going to do that little piece of chain rule at each little node that compute that took inputs and produced output we're going to store how we are going to chain the outputs gradient into the inputs gradients so by default this will be a function that doesn't do anything so and you can also see that here in the value in micro grad so we have this backward function by default doesn't do anything this is an empty function and that would be sort of the case for example for a leaf node for leaf node there's nothing to do but now if when we're creating these out values these out values are an addition of self and other and so we will want to sell set outs backward to be the function that propagates the gradient so let's define what should happen and we're going to store it in a closure let's define what should happen when we call outs grad for addition our job is to take outs grad and propagate it into selves grad and other dot grad so basically we want to solve self dot grad to something and we want to set others dot grad to something okay and the way we saw below how chain rule works we want to take the local derivative times the um sort of global derivative i should call it which is the derivative of the final output of the expression with respect to outs data with respect to out so the local derivative of self in an addition is 1.0 so it's just 1.0 times outs grad that's the chain rule and others dot grad will be 1.0 times out grad and what you basically what you're seeing here is that outs grad will simply be copied onto selves grad and others grad as we saw happens for an addition operation so we're going to later call this function to propagate the gradient having done an addition let's now do multiplication we're going to also define backward and we're going to set its backward to be backward and we want to chain out grad into self dot grad and others dot grad and this will be a little piece of chain rule for multiplication so we'll have so what should this be can you think through so what is the local derivative here the local derivative was others dot data and then oops others dot data and then times out dot grad that's channel and here we have self dot data times out dot grad that's what we've been doing and finally here for tan h that's backward and then we want to set outs backwards to be just backward and here we need to back propagate we have out dot grad and we want to chain it into self dot grad and self dot grad will be the local derivative of this operation that we've done here which is tan h and so we saw that the local gradient is 1 minus the tan h of x squared which here is t that's the local derivative because that's t is the output of this tan h so 1 minus t squared is the local derivative and then gradient has to be multiplied because of the chain rule so outs grad is chained through the local gradient into self dot grad and that should be basically it so we're going to redefine our value node we're going to swing all the way down here and we're going to redefine our expression make sure that all the grads are zero okay but now we don't have to do this manually anymore we are going to basically be calling the dot backward in the right order so first we want to call outs dot backward so o was the outcome of tan h right so calling those those backward will be this function this is what it will do now we have to be careful because there's a times out dot grad and out dot grad remember is initialized to zero so here we see grad zero so as a base case we need to set oath dot grad to 1.0 to initialize this with one and then once this is one we can call o dot backward and what that should do is it should propagate this grad through tan h so the local derivative times the global derivative which is initialized at one so this should um dope so i thought about redoing it but i figured i should just leave the error in here because it's pretty funny why is not an object not callable it's because i screwed up we're trying to save these functions so this is correct this here you don't want to call the function because that returns none these functions return none we just want to store the function so let me redefine the value object and then we're going to come back in redefine the expression draw dot everything is great o dot grad is one o dot grad is one and now now this should work of course okay so all that backward should this grad should now be 0.5 if we redraw and if everything went correctly 0.5 yay okay so now we need to call ns dot grad ns dot backward sorry ns backward so that seems to have worked so ns dot backward routed the gradient to both of these so this is looking great now we could of course called uh called b dot grad b dot backward sorry what's going to happen well b doesn't have a backward b's backward because b is a leaf node b's backward is by initialization the empty function so nothing would happen but we can call call it on it but when we call this one it's backward then we expect this 0.5 to get further routed right so there we go 0.5 0.5 and then finally we want to call it here on x2 w2 and on x1 w1 let's do both of those and there we go so we get 0.5 negative 1.5 and 1 exactly as we did before but now we've done it through calling that backward sort of manually so we have the one last piece to get rid of which is us calling underscore backward manually so let's think through what we are actually doing we've laid out a mathematical expression and now we're trying to go backwards through that expression so going backwards through the expression just means that we never want to call a dot backward for any node before we've done sort of everything after it so we have to do everything after it before we're ever going to call dot backward on any one node we have to get all of its full dependencies everything that it depends on has to propagate to it before we can continue back propagation so this ordering of graphs can be achieved using something called topological sort so topological sort is basically a laying out of a graph such that all the edges go only from left to right basically so here we have a graph it's a direct acyclic graph a dag and this is two different topological orders of it i believe where basically you'll see that it's a laying out of the nodes such that all the edges go only one way from left to right and implementing topological sort you can look in wikipedia and so on i'm not going to go through it in detail but basically this is what builds a topological graph we maintain a set of visited nodes and then we are going through starting at some root node which for us is o that's where we want to start the topological sort and starting at o we go through all of its children and we need to lay them out from left to right and basically this starts at o if it's not visited then it marks it as visited and then it iterates through all of its children and calls build topological on them and then after it's gone through all the children it adds itself so basically this node that we're going to call it on like say o is only going to add itself to the topo list after all of the children have been processed and that's how this function is guaranteeing that you're only going to be in the list once all your children are in the list and that's the invariant that is being maintained so if we built up on o and then inspect this list we're going to see that it ordered our value objects and the last one is the value of 0.707 which is the output so this is o and then this is n and then all the other nodes get laid out before it so that builds the topological graph and really what we're doing now is we're just calling dot underscore backward on all of the nodes in a topological order so if we just reset the gradients they're all zero what did we do we started by setting o dot grad to be one that's the base case then we built a topological order and then we went for node in reversed of topo now in in the reverse order because this list goes from you know we need to go through it in reversed order so starting at o node backward and this should be it there we go those are the correct derivatives finally we are going to hide this functionality so i'm going to copy this and we're going to hide it inside the value class because we don't want to have all that code lying around so instead of an underscore backward we're now going to define an actual backward so that backward without the underscore and that's going to do all the stuff that we just derived so let me just clean this up a little bit so we're first going to build a topological graph starting at self so build topo of self will populate the topological order into the topo list which is a local variable then we set self dot grads to be one and then for each node in the reversed list so starting at us and going to all the children underscore backward and that should be it so save come down here we define okay all the grads are zero and now what we can do is o dot backward without the underscore and there we go and that's uh that's back propagation place for one neuron now we shouldn't be too happy with ourselves actually because we have a bad bug and we have not surfaced the bug because of some specific conditions that we are we have to think about right now so here's the simplest case that shows the bug say i create a single node a and then i create a b that is a plus a and then i call backward so what's going to happen is a is three and then a b is a plus a so there's two arrows on top of each other here then we can see that b is of course the forward pass works b is just a plus a which is six but the gradient here is not actually correct that we calculate it automatically and that's because um of course uh just doing calculus in your head the derivative of b with respect to a should be uh two one plus one it's not one intuitively what's happening here right so b is the result of a plus a and then we call backward on it so let's go up and see what that does um b is the result of addition so out as b and then when we call backward what happened is self dot grad was set to one and then other that grad was set to one but because we're doing a plus a self and other are actually the exact same object so we are overriding the gradient we are setting it to one and then we are setting it again to one and that's why it stays at one so that's a problem there's another way to see this in a little bit more complicated expression so here we have a and b and then d will be the multiplication of the two and e will be the addition of the two and then we multiply e times d to get f and then we call f dot backward and these gradients if you check will be incorrect so fundamentally what's happening here again is basically we're going to see an issue any time we use a variable more than once until now in these expressions above every variable is used exactly once so we didn't see the issue but here if a variable is used more than once what's going to happen during backward pass we're back propagating from f to e to d so far so good but now e calls a backward and it deposits its gradients to a and b but then we come back to d and call backward and it overwrites those gradients at a and b so that's obviously a problem and the solution here if you look at the multivariate case of the chain rule and its generalization there the solution there is basically that we have to accumulate these gradients these gradients add and so instead of setting those gradients we can simply do plus equals we need to accumulate those gradients plus equals plus equals plus equals plus equals and this will be okay remember because we are initializing them at zero so they start at zero and then any contribution that flows backwards will simply add so now if we redefine this one because the plus equals this now works because a dot grad started at zero and we called b dot backward we deposit one and then we deposit one again and now this is two which is correct and here this will also work and we'll get correct gradients because when we call e dot backward we will deposit the gradients from this branch and then we get to back to d dot backward it will deposit its own gradients and then those gradients simply add on top of each other and so we just accumulate those gradients and that fixes the issue okay now before we move on let me actually do a bit of cleanup here and delete some of these some of this intermediate work so i'm not going to need any of this now that we've derived all of it um we are going to keep this because i want to come back to it delete the 10h delete our modeling example delete the step delete this keep the code that draws and then delete this example and leave behind only the definition of value and now let's come back to this non-linearity here that we implemented the 10h now i told you that we could have broken down 10h into its explicit atoms in terms of other expressions if we had the exp function so if you remember 10h is defined like this and we chose to develop 10h as a single function and we can do that because we know it's derivative and we can back propagate through it but we can also break down 10h into and express it as a function of exp and i would like to do that now because i want to prove to you that you get all the same results and all the same gradients um but also because it forces us to implement a few more expressions it forces us to do exponentiation addition subtraction division and things like that and i think it's a good exercise to go through a few more of these okay so let's scroll up to the definition of value and here one thing that we currently can't do is we can't do like a value of say 2.0 but we can't do you know here for example we want to add a constant one and we can't do something like this and we can't do it because it says int object has no attribute data that's because a plus one comes right here to add and then other is the integer one and then here python is trying to access one dot data and that's not a thing and that's because basically one is not a value object and we only have addition for value objects so as a matter of convenience so that we can create expressions like this and make them make sense we can simply do something like this basically we let other alone if other is an instance of value but if it's not an instance of value we're going to assume that it's a number like an integer or float and we're going to simply wrap it in in value and then other will just become value of other and then other will have a data attribute and this should work so if i just say this redefine value then this should work there we go okay and now let's do the exact same thing for multiply because we can't do something like this again for the exact same reason so we just have to go to mul and if other is not a value then let's wrap it in value let's redefine value and now this works now here's a kind of unfortunate and not obvious part a times two works we saw that but two times a is that going to work you'd expect it to right but actually it will not and the reason it won't is because python doesn't know like when when you do a times two basically um so a times two python will go and it will basically do something like a dot mul of two that's basically what it will call but to it two times a is the same as two dot mul of a and it doesn't two can't multiply value and so it's really confused about that so instead what happens is in python the way this works is you are free to define something called the armol and armol is kind of like a fallback so if a python can't do two times a it will check if um if by any chance a knows how to multiply two and that will be called into armol so because python can't do two times a it will check is there an armol in value and because there is it will now call that and what we'll do here is we will swap the order of the operands so basically two times a will redirect to armol and armol will basically call a times two and that's how that will work so redefining that with armol two times a becomes four okay now looking at the other elements that we still need we need to know how to exponentiate and how to divide so let's first do the explanation to the exponentiation part we're going to introduce a single function exp here and exp is going to mirror tanh in the sense that it's a simple single function that transforms a single scalar value and outputs a single scalar value so we pop out the python number we use math.exp to exponentiate it create a new value object everything that we've seen before the tricky part of course is how do you back propagate through e to the x and so here you can potentially pause the video and think about what should go here okay so basically we need to know what is the local derivative of e to the x so d by dx of e to the x is famously just e to the x and we've already just calculated e to the x and it's inside out that data so we can do out that data times and out that grad that's the chain rule so we're just chaining on to the current running grad and this is what the expression looks like it looks a little confusing but this is what it is and that's the exponentiation so redefining we should now be able to call a.exp and hopefully the backward pass works as well okay and the last thing we'd like to do of course is we'd like to be able to divide now i actually will implement something slightly more powerful than division because division is just a special case of something a bit more powerful so in particular just by rearranging if we have some kind of a b equals value of 4.0 here we'd like to basically be able to do a divide b and we'd like this to be able to give us 0.5 now division actually can be reshuffled as follows if we have a divide b that's actually the same as a multiplying 1 over b and that's the same as a multiplying b to the power of negative 1 and so what i'd like to do instead is i basically like to implement the operation of x to the k for some constant k so it's an integer or a float and we would like to be able to differentiate this and then as a special case negative 1 will be division and so i'm doing that just because it's more general and yeah you might as well do it that way so basically what i'm saying is we can redefine division which we will put here somewhere yeah we can put it here somewhere what i'm saying is that we can redefine division so self divide other this can actually be rewritten as self times other to the power of negative one and now value raised to the power of negative one we have now defined that so here's so we need to implement the pow function where am i going to put the pow function maybe here somewhere there's this coliform for it so this function will be called when we try to raise a value to some power and other will be that power now i'd like to make sure that other is only an int or a float usually other is some kind of a different value object but here other will be forced to be an int or a float otherwise the math won't work for for what we're trying to achieve in the specific case that would be a different derivative expression if we wanted other to be a value so here we create the up the value which is just uh you know this data raised to the power of other and other here could be for example negative one that's what we are hoping to achieve and then uh this is the backward stub and this is the fun part which is what is the uh chain rule expression here for back for um back propagating through the power function where the power is to the power of some kind of a constant so this is the exercise and maybe pause the video here and see if you can figure it out yourself as to what we should put here okay so um you can actually go here and look at derivative rules as an example and we see lots of derivative rules that you can hopefully know from calculus in particular what we're looking for is the power rule because that's telling us that if we're trying to take d by dx of x to the n which is what we're doing here then that is just n times x to the n minus one right okay so that's telling us about the local derivative of this power operation so all we want here basically n is now other and self.data is x and so this now becomes other which is n times self.data which is now a python int or a float it's not a value object we're accessing the data attribute raised to the power of other minus one or n minus one i can put brackets around this but this doesn't matter because power takes precedence over multiply and python so that would have been okay and that's the local derivative only but now we have to chain it and we change it just simply by multiplying by our top grand that's chain rule and this should technically work and we're going to find out soon but now if we do this this should now work and we get 0.5 so the forward pass works but does the backward pass work and i realized that we actually also have to know how to subtract so right now a minus b will not work to make it work we need one more piece of code here and basically this is the subtraction and the way we're going to implement subtraction is we're going to implement it by addition of a negation and then to implement negation we're going to multiply by negative one so just again using the stuff we've already built and just expressing it in terms of what we have and a minus b is not working okay so now let's scroll again to this expression here for this neuron and let's just compute the backward pass here once we've defined o and let's draw it so here's the gradients for all these leaf nodes for this two-dimensional neuron that has a 10h that we've seen before so now what i'd like to do is i'd like to break up this 10h into this expression here so let me copy paste this here and now instead of we'll preserve the label and we will change how we define o so in particular we're going to implement this formula here so we need e to the 2x minus 1 over e to the x plus 1 so e to the 2x we need to take 2 times n and we need to exponentiate it that's e to the 2x and then because we're using it twice let's create an intermediate variable e and then define o as e plus 1 over e minus 1 over e plus 1 e minus 1 over e plus 1 and that should be it and then we should be able to draw dot of o so now before i run this what do we expect to see number one we're expecting to see a much longer graph here because we've broken up 10h into a bunch of other operations but those operations are mathematically equivalent and so what we're expecting to see is number one the same result here so the forward pass works and number two because of that mathematical equivalence we expect to see the same backward pass and the same gradients on these leaf nodes so these gradients should be identical so let's run this so number one let's verify that instead of a single 10h node we have now exp and we have plus we have times negative one this is the division and we end up with the same forward pass here and then the gradients we have to be careful because they're in slightly different order potentially the gradients for w2 x2 should be 0 and 0.5 w2 and x2 are 0 and 0.5 and w1 x1 are 1 and negative 1.5 1 and negative 1.5 so that means that both our forward passes and backward passes were correct because this turned out to be equivalent to 10h before and so the reason I wanted to go through this exercise is number one we got to practice a few more operations and writing more backwards passes and number two I wanted to illustrate the point that the level at which you implement your operations is totally up to you you can implement backward passes for tiny expressions like a single individual plus or a single times or you can implement them for say 10h which is a kind of a potentially you can see it as a composite operation because it's made up of all these more atomic operations but really all of this is kind of like a fake concept all that matters is we have some kind of inputs and some kind of an output and this output is a function of the inputs in some way and as long as you can do forward pass and the backward pass of that little operation it doesn't matter what that operation is and how composite it is if you can write the local gradients you can chain the gradient and you can continue back propagation so the design of what those functions are is completely up to you so now I would like to show you how you can do the exact same thing but using a modern deep neural network library like for example PyTorch which I've roughly modeled micro grad by and so PyTorch is something you would use in production and I'll show you how you can do the exact same thing but in PyTorch API so I'm just going to copy paste it in and walk you through it a little bit this is what it looks like so we're going to import PyTorch and then we need to define these value objects like we have here now micro grad is a scalar valued engine so we only have scalar values like 2.0 but in PyTorch everything is based around tensors and like I mentioned tensors are just n-dimensional arrays of scalars so that's why things get a little bit more complicated here I just need a scalar valued tensor a tensor with just a single element but by default when you work with PyTorch you would use more complicated tensors like this so if I import PyTorch then I can create tensors like this and this tensor for example is a two by three array of scalars in a single compact representation so you can check its shape we see that it's a two by three array and so on so this is usually what you would work with in the actual libraries so here I'm creating a tensor that has only a single element 2.0 and then I'm casting it to be double because Python is by default using double precision for its floating point numbers so I'd like everything to be identical by default the data type of these tensors will be float 32 so it's only using a single precision float so I'm casting it to double so that we have float 64 just like in Python so I'm casting to double and then we get something similar to value of 2.0 the next thing I have to do is because these are leaf nodes by default PyTorch assumes that they do not require gradients so I need to explicitly say that all of these nodes require gradients okay so this is going to construct scalar valued one element tensors make sure that PyTorch knows that they require gradients now by default these are set to false by the way because of efficiency reasons because usually you would not want gradients for leaf nodes like the inputs to the network and this is just trying to be efficient in the most common cases so once we've defined all of our values in PyTorch land we can perform arithmetic just like we can here in micrograd land so this would just work and then there's a torch.tanh also and when we get back as a tensor again and we can just like in micrograd it's got a data attribute and it's got grad attributes so these tensor objects just like in micrograd have a dot data and a dot grad and the only difference here is that we need to call a dot item because otherwise PyTorch dot item basically takes a single tensor of one element and it just returns that element stripping out the tensor so let me just run this and hopefully we are going to get this is going to print the forward pass which is 0.707 and this will be the gradients which hopefully are 0.50 negative 1.5 and 1 so if we just run this there we go 0.7 so the forward pass agrees and then 0.50 negative 1.5 and 1 so PyTorch agrees with us and just to show you here basically oh here's a tensor with a single element and it's a double and we can call dot item on it to just get the single number out so that's what item does and o is a tensor object like i mentioned and it's got a backward function just like we've implemented and then all of these also have a dot grad so like x2 for example has a grad and it's a tensor and we can pop out the individual number with dot item so basically Torches Torch can do what we did in micro grad as a special case when your tensors are all single element tensors but the big deal with PyTorch is that everything is significantly more efficient because we are working with these tensor objects and we can do lots of operations in parallel on all of these tensors but otherwise what we've built very much agrees with the API of PyTorch okay so now that we have some machinery to build out pretty complicated mathematical expressions we can also start building up neural nets and as I mentioned neural nets are just a specific class of mathematical expressions so we're going to start building out a neural net piece by piece and eventually we'll build out a two-layer multi-layer layer perceptron as it's called and I'll show you exactly what that means let's start with a single individual neuron we've implemented one here but here I'm going to implement one that also subscribes to the PyTorch API in how it designs its neural network modules so just like we saw that we can like match the API of PyTorch on the autograd side we're going to try to do that on the neural network modules so here's class neuron and just for the sake of efficiency I'm going to copy paste some sections that are relatively straightforward so the constructor will take number of inputs to this neuron which is how many inputs come to a neuron so this one for example has three inputs and then it's going to create a weight that is some random number between negative one and one for every one of those inputs and a bias that controls the overall trigger happiness of this neuron and then we're going to implement a def underscore underscore call of self and x sum input x and really what we don't want to do here is w times x plus b where w times x here is a dot product specifically now if you haven't seen call let me just return 0.0 here for now the way this works now is we can have an x which is say like 2.0 3.0 then we can initialize a neuron that is two-dimensional because these are two numbers and then we can feed those two numbers into that neuron to get an output and so when you use this notation n of x python will use call so currently call just returns 0.0 now we'd like to actually do the forward pass of this neuron instead so we're going to do here first is we need to basically multiply all of the elements of w with all of the elements of x pairwise we need to multiply them so the first thing we're going to do is we're going to zip up salta w and x and in python zip takes two iterators and it creates a new iterator that iterates over the tuples of their corresponding entries so for example just to show you we can print this list and still return 0.0 here sorry i'm in my so we see that these w's are paired up with the x's w with x and now what we want to do is for wi xi in we want to multiply w times wi times xi and then we want to sum all of that together to come up with an activation and add also salta b on top so that's the raw activation and then of course we need to pass that through a non-linearity so what we're going to be returning is act dot 10h and here's out so now we see that we are getting some outputs and we get a different output from a neuron each time because we are initializing different weights and biases and then to be a bit more efficient here actually sum by the way takes a second optional parameter which is the start and by default the start is zero so these elements of this sum will be added on top of zero to begin with but actually we can just start with cell.b and then we just have an expression like this and then the generator expression here must be parenthesized in python there we go yep so now we can forward a single neuron next up we're going to define a layer of neurons so here we have a schematic for a MLP so we see that these MLPs each layer this is one layer has actually a number of neurons and they're not connected to each other but all of them are fully connected to the input so what is a layer of neurons it's just it's just a set of neurons evaluated independently so in the interest of time i'm going to do something fairly straightforward here it's literally a layer is just a list of neurons and then how many neurons do we have we take that as an input argument here how many neurons do you want in your layer number of outputs in this layer and so we just initialize completely independent neurons with this given dimensionality and when we call on it we just independently evaluate them so now instead of a neuron we can make a layer of neurons they are two-dimensional neurons and let's have three of them and now we see that we have three independent evaluations of three different neurons right okay and finally let's complete this picture and define an entire multi-layer perceptron or MLP and as we can see here in an MLP these layers just feed into each other sequentially so let's come here and i'm just going to copy the code here in interest of time so an MLP is very similar we're taking the number of inputs as before but now instead of saying taking a single n out which is number of neurons in a single layer we're going to take a list of n outs and this list defines the sizes of all the layers that we want in our MLP so here we just put them all together and then iterate over consecutive pairs of these sizes and create layer objects for them and then in the call function we are just calling them sequentially so that's an MLP really and let's actually re-implement this picture so we want three input neurons and then two layers of four and an output unit so we want a three-dimensional input say this is an example input we want three inputs into two layers of four and one output and this of course is an MLP and there we go that's a forward pass of an MLP to make this a little bit nicer you see how we have just a single element but it's wrapped in a list because layer always returns lists so for convenience return outs at zero if len outs is exactly a single element else return fullest and this will allow us to just get a single value out at the last layer that only has a single neuron and finally we should be able to draw dot of n of x and as you might imagine these expressions are now getting relatively involved so this is an entire MLP that we're defining now all the way until a single output okay and so obviously you would never differentiate on pen and paper these expressions but with micrograd we will be able to back propagate all the way through this and back propagate into these weights of all these neurons so let's see how that works okay so let's create ourselves a very simple example data set here so this data set has four examples and so we have four possible inputs into the neural net and we have four desired targets so we'd like the neural net to assign or output 1.0 when it's fed this example negative one when it's fed these examples and one when it's fed this example so it's a very simple binary classifier neural net basically that we would like here now let's think what the neural net currently thinks about these four examples we can just get their predictions basically we can just call n of x for x and x's and then we can print so these are the outputs of the neural net on those four examples so the first one is 0.91 but we'd like it to be 1 so we should push this one higher this one we want to be higher this one says 0.88 and we want this to be negative 1 this is 0.88 we want it to be negative 1 and this one is 0.88 we want it to be 1 so how do we make the neural net and how do we tune the weights to better predict the desired targets and the trick used in deep learning to achieve this is to calculate a single number that somehow measures the total performance of your neural net and we call this single number the loss so the loss first is a single number that we're going to define that basically measures how well the neural net is performing right now we have the intuitive sense that it's not performing very well because we're not very much close to this so the loss will be high and we'll want to minimize the loss so in particular in this case what we're going to do is we're going to implement the mean squared error loss so what this is doing is we're going to basically iterate for y ground truth and y output in zip of y's and y_red so we're going to pair up the ground truths with the predictions and the zip iterates over tuples of them and for each y ground truth and y output we're going to subtract them and square them so let's first see what these losses are these are individual loss components and so basically for each one of the four we are taking the prediction and the ground truth we are subtracting them and squaring them so because this one is so close to its target 0.91 is almost one subtracting them gives a very small number so here we would get like a negative 0.1 and then squaring it just makes sure that regardless of whether we are more negative or more positive we always get a positive number instead of squaring we should we could also take for example the absolute value we need to discard the sign and so you see that the expression is ranged so that you only get zero exactly when y out is equal to y ground truth when those two are equal so your prediction is exactly the target you are going to get zero and if your prediction is not the target you are going to get some other number so here for example we are way off and so that's why the loss is quite high and the more off we are the greater the loss will be so we don't want high loss we want low loss and so the final loss here will be just the sum of all of these numbers so you see that this should be zero roughly plus zero roughly but plus seven so loss should be about seven here and now we want to minimize the loss we want the loss to be low because if loss is low then every one of the predictions is equal to its target so the loss the lowest it can be is zero and the greater it is the worse off the neural net is predicting so now of course if we do loss.backward something magical happened when i hit enter and the magical thing of course that happened is that we can look at n.layers.neuron and that layers at say like the first layer that neurons at zero because remember that mlp has the layers which is a list and each layer has neurons which is a list and that gives us an individual neuron and then it's got some weights and so we can for example look at the weights at zero oops it's not called weights it's called w and that's a value but now this value also has a grad because of the backward pass and so we see that because this gradient here on this particular weight of this particular neuron of this particular layer is negative we see that its influence on the loss is also negative so slightly increasing this particular weight of this neuron of this layer would make the loss go down and we actually have this information for every single one of our neurons and all their parameters actually it's worth looking at also the draw dot of loss by the way so previously we looked at the draw dot of a single neuron neuron forward pass and that was already a large expression but what is this expression we actually forwarded every one of those four examples and then we have the loss on top of them with the mean squared error and so this is a really massive graph because this graph that we've built up now oh my gosh this graph that we've built up now which is kind of excessive it's excessive because it has four forward passes of a neural net for every one of the examples and then it has the loss on top and it ends with the value of the loss which was 7.12 and this loss will now back propagate through all the four forward passes all the way through just every single intermediate value of the neural net all the way back to of course the parameters of the weights which are the input so these weight parameters here are inputs to this neural net and these numbers here these scalars are inputs to the neural net so if we went around here we will probably find some of these examples this 1.0 potentially maybe this 1.0 or you know some of the others and you'll see that they all have gradients as well the thing is these gradients on the input data are not that useful to us and that's because the input data seems to be not changeable it's it's a given to the problem and so it's a fixed input we're not going to be changing it or messing with it even though we do have gradients for it but some of these gradients here will be for the neural network parameters the w's and the b's and those we of course we want to change okay so now we're going to want some convenience code to gather up all of the parameters of the neural net so that we can operate on all of them simultaneously and every one of them we will nudge a tiny amount based on the gradient information so let's collect the parameters of the neural net all in one array so let's create a parameters of self that just returns self.w which is a list concatenated with a list of self.b so this will just return a list list plus list just you know gives you a list so that's parameters of neuron and i'm calling it this way because also pytorch has a parameters on every single nn module and it does exactly what we're doing here it just returns the parameter tensors for us it's the parameter scalars now layer is also a module so it will have parameters self and basically what we want to do here is something like this like params is here and then for neuron in self.neurons we want to get neuron.parameters and we want to params.extend right so these are the parameters of this neuron and then we want to put them on top of params so params.extend of piece and then we want to return params so this there's way too much code so actually there's a way to simplify this which is return p for neuron in self.neurons for p in neuron.parameters so it's a single list comprehension in python you can sort of nest them like this and you can then create the desired array so this is these are identical we can take this out and then let's do the same here def parameters self and return a parameter for layer in self.layers for p in layer.parameters and that should be good now let me pop out this so we don't re-initialize our network because we need to re-initialize our okay so unfortunately we will have to probably re-initialize the network because we just had functionality because this class of course we i want to get all the end up parameters but that's not going to work because this is the old class okay so unfortunately we do have to re-initialize the network which will change some of the numbers but let me do that so that we pick up the new api we can now do end up parameters and these are all the weights and biases inside the entire neural net so in total this mlp has 41 parameters and now we'll be able to change them if we recalculate the loss here we see that unfortunately we have slightly different predictions and slightly different loss um but that's okay okay so we see that this neuron's gradient is slightly negative we can also look at its data right now which is 0.85 so this is the current value of this neuron and this is its gradient on the loss so what we want to do now is we want to iterate for every p in end up parameters so for all the 41 parameters of this neural net we actually want to change p.data slightly according to the gradient information okay so dot dot dot to do here but this will be basically a tiny update in this gradient descent scheme and gradient descent we are thinking of the gradient as a vector pointing in the direction of increased loss and so in gradient descent we are modifying p.data by a small step size in the direction of the gradient so the step size as an example could be like a very small number like 0.01 is the step size times p.grad right but we have to think through some of the signs here so in particular working with this specific example here we see that if we just left it like this then this neuron's value would be currently increased by a tiny amount of the gradient the gradient is negative so this value of this neuron would go slightly down it would become like 0.84 or something like that but if this neuron's value goes lower that would actually increase the loss that's because the derivative of this neuron is negative so increasing this makes the loss go down so increasing it is what we want to do instead of decreasing it so basically what we're missing here is we're actually missing a negative sign and again this other interpretation and that's because we want to minimize the loss we don't want to maximize the loss we want to decrease it and the other interpretation as i mentioned is you can think of the gradient vector so basically just the vector of all the gradients as pointing in the direction of increasing the loss but then we want to decrease it so we actually want to go in the opposite direction and so you can convince yourself that this sort of like does the right thing here with the negative because we want to minimize the loss so if we nudge all the parameters by a tiny amount then we'll see that this data will have changed a little bit so now this neuron is a tiny amount greater value so 0.854 went to 0.857 and that's a good thing because slightly increasing this neuron data makes the loss go down according to the gradient and so the correcting has happened sine wise and so now what we would expect of course is that because we've changed all these parameters we expect that the loss should have gone down a bit so we want to re-evaluate the loss let me basically this is just a data definition that hasn't changed but the forward pass here of the network we can recalculate and actually let me do it outside here so that we can compare the two loss values so here if i recalculate the loss we'd expect the new loss now to be slightly lower than this number so hopefully what we're getting now is a tiny bit lower than 4.36 okay and remember the way we've arranged this is that low loss means that our predictions are matching the targets so our predictions now are probably slightly closer to the targets and now all we have to do is we have to iterate this process so again we've done the forward pass and this is the loss now we can loss that backward let me take these out and we can do a step size and now we should have a slightly lower loss 4.36 goes to 3.9 and okay so we've done the forward pass here's the backward pass nudge and now the loss is 3.66 3.47 and you get the idea we just continue doing this and this is gradient descent we're just iteratively doing forward pass backward pass update forward pass backward pass update and the neural net is improving its predictions so here if we look at y pred now y pred we see that this value should be getting closer to one so this value should be getting more positive these should be getting more negative and this one should be also getting more positive so if we just iterate this a few more times actually we may be able to afford to go a bit faster let's try a slightly higher learning rate oops okay there we go so now we're at 0.31 if you go too fast by the way if you try to make it too big of a step you may actually overstep overconfidence because again remember we don't actually know exactly about the loss function the loss function has all kinds of structure and we only know about the very local dependence of all these parameters on the loss but if we step too far we may step into you know a part of the loss that is completely different and that can destabilize training and make your loss actually blow up even so the loss is now 0.04 so actually the predictions should be really quite close let's take a look so you see how this is almost one almost negative one almost one we can continue going so yep backward update oops there we go so we went way too fast and we actually overstepped so we got too eager where are we now oops okay 7e negative 9 so this is very very low loss and the predictions are basically perfect so somehow we basically we were doing way too big updates and we briefly exploded but then somehow we ended up getting into a really good spot so usually this learning rate and the tuning of it is a subtle art you want to set your learning rate if it's too low you're going to take way too long to converge but if it's too high the whole thing gets unstable and you might actually even explode the loss depending on your loss function so finding the step size to be just right it's it's a pretty subtle art sometimes when you're using sort of vanilla gradient descent but we happen to get into a good spot we can look at n dot parameters so this is the setting of weights and biases that makes our network predict the desired targets very very close and basically we've successfully trained a neural net okay let's make this a tiny bit more respectable and implement an actual training loop and what that looks like so this is the data definition that stays this is the forward pass so for k in range you know we're going to take a bunch of steps first you do the forward pass we validate the loss let's reinitialize the neural net from scratch and here's the data and we first do forward pass then we do the backward pass and then we do an update that's gradient descent and then we should be able to iterate this and we should be able to print the current step the current loss let's just print the sort of number of the loss and that should be it and then the learning rate 0.01 is a little too small 0.1 we saw is like a little bit dangerous with ui let's go somewhere in between and we'll optimize this for not 10 steps but let's go for say 20 steps let me erase all of this junk and let's run the optimization and you see how we've actually converged slower in a more controlled manner and got to a loss that is very low so i expect y_pred to be quite good there we go and that's it okay so this is kind of embarrassing but we actually have a really terrible bug in here and it's a subtle bug and it's a very common bug and i can't believe i've done it for the 20th time in my life especially on camera and i could have re-shot the whole thing but i think it's pretty funny and you know you get to appreciate a bit what working with neural nuts maybe is like sometimes we are guilty of a common bug i've actually tweeted the most common neural mistakes a long time ago now and i'm not really gonna explain any of these except for we are guilty of number three you forgot to zero grad before dot backward what is that basically what's happening and it's a subtle bug and i'm not sure if you saw it is that all of these weights here have a dot data and a dot grad and the dot grad starts at zero and then we do backward and we fill in the gradients and then we do an update on the data but we don't flush the grad it stays there so when we do the second forward pass and we do backward again remember that all the backward operations do a plus equals on the grad and so these gradients just add up and they never get reset to zero so basically we didn't zero grad so here's how we zero grad before backward we need to iterate over all the parameters and we need to make sure that p dot grad is set to zero we need to reset it to zero just like it is in the constructor so remember all the way here for all these value nodes grad is reset to zero and then all these backward passes do a plus equals from that grad but we need to make sure that we reset these graphs to zero so that when we do backward all of them start at zero and the actual backward pass accumulates the loss derivatives into the grads so this is zero grad in pytorch and we will slightly we'll get a slightly different optimization let's reset the neural net the data is the same this is now i think correct and we get a much more you know we get a much more slower descent we still end up with pretty good results and we can continue this a bit more to get down lower and lower and lower yeah so the only reason that the previous thing worked it's extremely buggy the only reason that worked is that this is a very very simple problem and it's very easy for this neural net to fit this data and so the grads ended up accumulating and it effectively gave us a massive step size and it made us converge extremely fast but basically now we have to do more steps to get to very low values of loss and get y pred to be really good we can try to step a bit greater yeah we're gonna get closer and closer to one minus one and one so working with neural nets is sometimes tricky because you may have lots of bugs in the code and your network might actually work just like ours worked but chances are is that if we had a more complex problem then actually this bug would have made us not optimize the loss very well and we were only able to get away with it because the problem is very simple so let's now bring everything together and summarize what we learned what are neural nets neural nets are these mathematical expressions fairly simple mathematical expressions in the case of multilear perceptron that take input as the data and they take input the weights and the parameters of the neural net mathematical expression for the forward pass followed by a loss function and the loss function tries to measure the accuracy of the predictions and usually the loss will be low when your predictions are matching your targets or where the network is basically behaving well so we we manipulate the loss function so that when the loss is low the network is doing what you want it to do on your problem and then we backward the loss use back propagation to get the gradient and then we know how to tune all the parameters to decrease the loss locally but then we have to iterate that process many times in what's called the gradient descent so we simply follow the gradient information and that minimizes the loss and the loss is arranged so that when the loss is minimized the network is doing what you want it to do and yeah so we just have a blob of neural stuff and we can make it do arbitrary things and that's what gives neural nets their power it's you know this is a very tiny network with 41 parameters but you can build significantly more complicated neural nets with billions at this point almost trillions of parameters and it's a massive blob of neural tissue simulated neural tissue roughly speaking and you can make it do extremely complex problems and these neural nets then have all kinds of very fascinating emergent properties in when you try to make them do significantly hard problems as in the case of gpt for example we have massive amounts of text from the internet and we're trying to get a neural net to predict to take like a few words and try to predict the next word in a sequence that's the learning problem and it turns out that when you train this on all of internet the neural net actually has like really remarkable emergent properties but that neural net would have hundreds of billions of parameters but it works on fundamentally the exact same principles the neural net of course will be a bit more complex but otherwise the evaluating the gradient is there and will be identical and the gradient descent would be there and would be basically identical but people usually use slightly different updates this is a very simple stochastic gradient descent update and the loss function would not be a mean squared error they would be using something called the cross entropy loss for predicting the next token so there's a few more details but fundamentally the neural network setup and neural network training is identical and pervasive and now you understand intuitively how that works under the hood in the beginning of this video i told you that by the end of it you would understand everything in micrograd and then would slowly build it up let me briefly prove that to you so i'm going to step through all the code that is in micrograd as of today actually potentially some of the code will change by the time you watch this video because i intend to continue developing micrograd but let's look at what we have so far at least init.py is empty when you go to engine.py that has the value everything here you should mostly recognize so we have the data.data.grad attributes we have the backward function we have the previous set of children and the operation that produced this value we have addition multiplication and raising to a scalar power we have the relu non-linearity which is slightly different type of non-linearity than tanh that we used in this video both of them are non-linearities and notably tanh is not actually present in micrograd as of right now but i intend to add it later we have the backward which is identical and then all of these other operations which are built up on top of operations here so value should be very recognizable except for the non-linearity used in this video there's no massive difference between relu and tanh and sigmoid and these other non-linearities they're all roughly equivalent and can be used in MLPs so i use tanh because it's a bit smoother and because it's a little bit more complicated than relu and therefore it's stressed a little bit more the local gradients and working with those derivatives which i thought would be useful and then .py is the neural networks library as i mentioned so you should recognize identical implementation of neuron layer and MLP notably or not so much we have a class module here there's a parent class of all these modules i did that because there's an nn.module class in pytorch and so this exactly matches that api and nn.module in pytorch has also a zero grad which i refactored out here so that's the end of micrograd really then there's a test which you'll see basically creates two chunks of code one in micrograd and one in pytorch and we'll make sure that the forward and the backward paths agree identically for a slightly less complicated expression a slightly more complicated expression everything agrees so we agree with pytorch and all of these operations and finally there's a demo.pypy.ymb here and it's a bit more complicated binary classification demo than the one i covered in this lecture so we only had a tiny data set of four examples here we have a bit more complicated example with lots of blue points and lots of red points and we're trying to again build a binary classifier to distinguish two-dimensional points as red or blue it's a bit more complicated MLP here with it's a bigger MLP the loss is a bit more complicated because it supports batches so because our data set was so tiny we always did a forward pass on the entire data set of four examples but when your data set is like a million examples what we usually do in practice is we basically pick out some random subset we call that a batch and then we only process the batch forward backward and update so we don't have to forward the entire training set so this supports batching because there's a lot more examples here we do a forward pass the loss is slightly more different this is a max margin loss that i implement here the one that we used was the mean squared error loss because it's the simplest one there's also the binary cross-entropy loss all of them can be used for binary classification and don't make too much of a difference in the simple examples that we looked at so far there's something called L2 regularization used here this has to do with generalization of the neural net and controls the overfitting in machine learning setting but i did not cover these concepts in concepts in this video potentially later and the training loop you should recognize so forward backward with zero grad and update and so on you'll notice that in the update here the learning rate is scaled as a function of number of iterations and it shrinks and this is something called learning rate decay so in the beginning you have a high learning rate and as the network sort of stabilizes near the end you bring down the learning rate to get some of the fine details in the end and in the end we see the decision surface of the neural net and we see that it learns to separate out the red and the blue area based on the data points so that's the slightly more complicated example in the demo demo.hypeiymb that you're free to go over but yeah as of today that is micrograd i also wanted to show you a little bit of real stuff so that you get to see how this is actually implemented in a production grade library like pytorch so in particular i wanted to show i wanted to find and show you the backward pass for 10h in pytorch so here in micrograd we see that the backward pass for 10h is 1 minus t square where t is the output of the 10h of x times of that grad which is the chain rule so we're looking for something that looks like this now i went to pytorch which has an open source github codebase and i looked through a lot of its code and honestly i i spent about 15 minutes and i couldn't find 10h and that's because these libraries unfortunately they grow in size and entropy and if you just search for 10h you get apparently 2800 results and 400 and 406 files so i don't know what these files are doing honestly and why there are so many mentions of 10h but unfortunately these libraries are quite complex they're meant to be used not really inspected eventually i did stumble on someone who tries to change the 10h backward code for some reason and someone here pointed to the cpu kernel and the cuda kernel for 10h backward so this so basically depends on if you're using pytorch on a cpu device or on a gpu which these are different devices and i haven't covered this but this is the 10h backward kernel for cpu and the reason it's so large is that number one this is like if you're using a complex type which we haven't even talked about if you're using a specific data type of bfloat16 which we haven't talked about and then if you're not then this is the kernel and deep here we see something that resembles our backward pass so they have a times 1 minus b square so this b b here must be the output of the 10h and this is the out.grad so here we found it deep inside pytorch on this location for some reason inside binary ops kernel when 10h is not actually binary op and then this is the gpu kernel we're not complex we're here and here we go with one line of code so we did find it but basically unfortunately these code bases are very large and micrograd is very very simple but if you actually want to use real stuff finding the code for it you'll actually find that difficult i also wanted to show you a little example here where pytorch is showing you how you can register a new type of function that you want to add to pytorch as a lego building block so here if you want to for example add a legendre polynomial 3 here's how you could do it you will register it as a class that subclasses torch.rgrad.function and then you have to tell pytorch how to forward your new function and how to backward through it so as long as you can do the forward pass of this little function piece that you want to add and as long as you know the the local derivative the local gradients which are implemented in the backward pytorch will be able to back propagate through your function and then you can use this as a lego block in a larger lego castle of all the different lego blocks that pytorch already has and so that's the only thing you have to tell pytorch and everything would just work and you can register new types of functions in this way following this example and that is everything that i wanted to cover in this lecture so i hope you enjoyed building out micrograd with me i hope you find it interesting insightful and yeah i will post a lot of the links that are related to this video in the video description below i will also probably post a link to a discussion forum or discussion group where you can ask questions related to this video and then i can answer or someone else can answer your questions and i may also do a follow-up video that answers some of the most common questions but for now that's it i hope you enjoyed it if you did then please like and subscribe so that youtube knows to feature this video to more people and that's it for now i'll see you later now here's the problem we know dl by wait what is the problem and that's everything i wanted to cover in this lecture so i hope you enjoyed us building up micro grabbed micro grab okay now let's do the exact same thing for multiply because we can't do something like a times two whoops i know what happened there